卡尔曼滤波解卷积算法的优化问题*
闫晓瑾,何国荣,梅铁民
(沈阳理工大学自动化与电气工程学院,辽宁 沈阳 110159)
0 引言
信号解卷积是信号处理领域中一个重要的研究内容,其广泛应用于图像处理、语音信号处理、阵列信号处理、地震波信号处理、生物医学、故障诊断等领域。在这些领域中,通常观测信号是源信号与一线性系统冲激响应的卷积,解卷积就是从观测信号中恢复源信号或系统冲激响应的过程。
已有的解卷积算法大致可分为两类,一类是房间冲激响应未知情况下的盲解卷积算法,另一类是房间冲激响应已知的解卷积算法。盲解卷积是指在房间冲激响应未知或不需要估计的情况下,由观测信号直接估计解卷积滤波器。Bussgang 算法[1]是自适应信号处理领域中最经典的盲解卷积算法,该算法实现简单且收敛速度快,但该算法需要源信号和解卷积噪声的统计特性等先验知识。针 对SISO(Single Input Single Output)系 统,文献[2]将观测信号转化为复基带信号,然后利用最小均方算法(Least Mean Square,LMS)来实现盲解卷积,该算法适用于高斯信号和非高斯信号,对源信号的适用面较宽,但仍然存在收敛速度和计算复杂度之间的矛盾问题。在生物医学中,心电图信号、脉搏信号等可以被认为是心跳信号与人体系统的卷积,通过对心电图信号进行解卷积处理即可获得病人的心跳信号,文献[3]中利用递归最小二乘算法(Recursive least squares,RLS)来求解卷积滤波器,利用定点卷积核补偿(Fixed-point convolution kernel compensation,FP-CKC)求出RLS算法的期望信号,利用粒子群优化算法(Particle Swarm optimization,PSO)求出逆滤波器的初始值,该算法可用于较高的噪声水平。在语音去混响领域中,解卷积过程是其中重要的一部分。文献[4]根据声源语音信号的短时傅里叶变换系数的稀疏性,将非负矩阵分解(Non-negative Matrix Factorization,NMF)应用到多通道线性预测(Multi-Channel Linear Prediction,MCLP)中来达到去混响的目的,该算法取得不错的效果,不足之处在于明显增加了计算量。在轴承故障诊断领域中,振动信号是由故障引起的周期性冲击信号与机械部件的共振响应卷积的结果,传统的解卷积方法有最大相关峭度解卷积算法(Maximum Correlated Kurtosis Deconvolution,MCKD),该算法的解卷积信号的包络谱中可以呈现出典型的周期性脉冲的特点[5]。文献[6]提出最小熵解卷积算法(Mimum-Entropy Deconvolution,MED),该算法可适用于非最小相位系统,但要求源信号具有简单稀疏的统计特性。除此之外,还有基于稀疏表示的盲解卷积算法[7]、子空间分解的盲解卷积方法[8]等。在语音去混响解卷积算法中,通常先估计出房间冲激响应,然后再进行解卷积。在SISO 系统中,文献[9]利用复倒谱技术估计出房间冲激响应,并在倒谱域内求其逆滤波器,然后将其逆滤波器作为改进的自然梯度算法的初始值来进行迭代解卷积。MINT(the multiple-input/output inverse-filtering theorem)定理是Miyoshi 等人提出的在房间冲激响应已知的情况下求逆滤波器的一种经典方法[10],文献[11]和[12]利用观测信号的自相关矩阵来获得房间冲激响应的先验知识,然后根据MINT 定理来求逆滤波器,但该算法要求源信号是平稳的白噪声信号。其实,利用MINT 定理求逆滤波器的方法在实际中并不可行,因为该方法对噪声非常敏感,针对此问题,文献[13]提出在子带最小二乘算法中使用正则化,该算法可以降低逆滤波器对房间冲激响应的估计误差和对观测噪声的敏感度。文献[14]通过观测信号的二阶累积量估计出非最小相位系统的房间冲激响应,对其卷积矩阵直接求逆,该方法在高阶系统时的计算量将非常大。文献[15]在估计出房间冲激响应后,利用p-范数和窗函数来求逆滤波器,进而实现解卷积。文献[16]给出了在估计出房间冲激响应的情况下不求逆滤波器的解卷积算法,利用卡尔曼滤波算法直接进行解卷积,该算法具有较高的噪声稳定性,但其缺点是计算量大。
本文在卡尔曼滤波解卷积算法的基础上,提出了一种降低计算量的优化算法,该算法在保证算法稳定性的同时,又能大幅度减少计算量。该算法不仅可以用于语音去混响,还可以应用在其他领域。
1 标准的卡尔曼滤波解卷积算法
1.1 数学模型
在单输入多输出系统(Single Input Multiple Output,SIMO)中,观测信号是声源信号和房间冲激响应的卷积,那么,观测信号可以表示为:
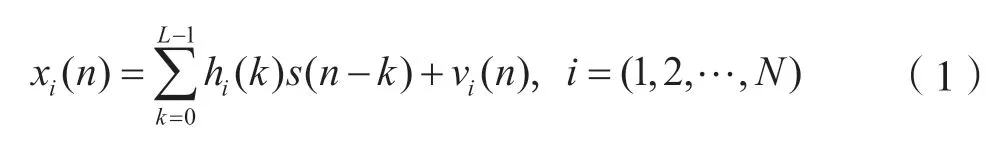
其中,s(n)表示声源信号,n为时间,hi表示第i路房间冲激响应,xi(n)表示第i路麦克风接收的观测信号,vi(n)表示第i路观测噪声,L为房间冲激响应的长度,N为麦克风的数量。
利用(1)式建立卡尔曼滤波的状态方程和观测方程:
状态方程:
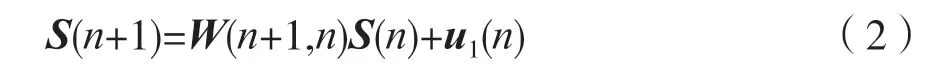
测量方程:

其中S(n)为n时刻的状态矢量,由声源信号s(n)构成状态矢量S(n)=[s(n),s(n-1),…,s(n-L+1)]T;X(n)=[x1(n),x2(n),…,xN(n)]T为n时刻的观测矢量;观测矩阵由N路房间冲激响应构成,是一个N×L维矩阵(其中hi=[hi(0),hi(1),…,hi(L-1)]T);u1(n)和u2(n)分别为均值为零的过程白噪声和观测白噪声,它们的协方差矩阵分别为和(I为单位矩阵);W(n+1,n)为L×L维状态转移矩阵,定义为:

并且,W(n,n+1)=WT(n+1,n)。
1.2 标准的卡尔曼滤波解卷积算法
已知房间冲激响应(h1,h2,...hN),在一个解卷积块中的标准卡尔曼滤波解卷积算法的迭代过程列于表1 中。
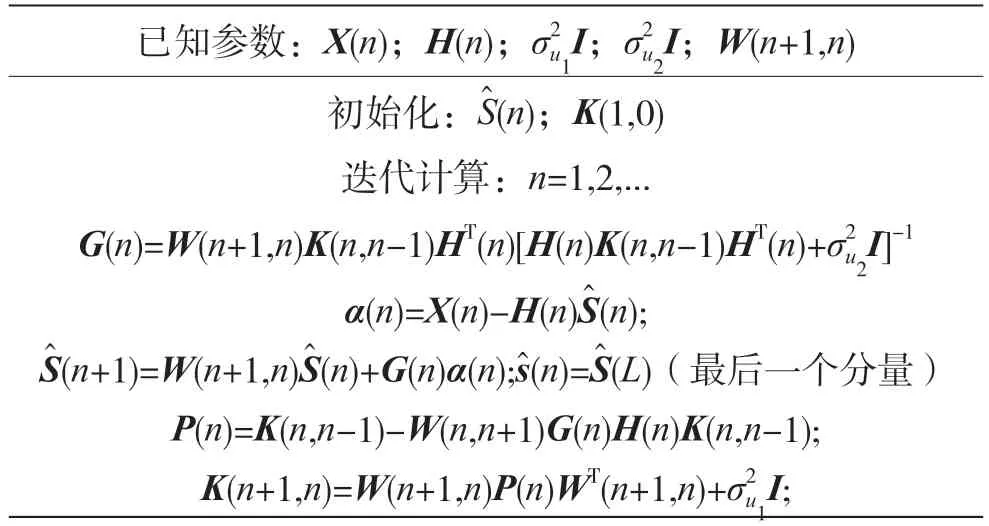
表1 标准卡尔曼滤波解卷积算法
其中G(n)为卡尔曼增益,P(n)为滤波的状态矢量估计误差的自相关矩阵,K(n+1,n)为状态矢量一步预测误差的自相关矩阵,α(n)为新息。卡尔曼滤波器输出的n时刻的声源信号的最后一个分量。
标准卡尔曼滤波算法中五个变量迭代一次的计算量统计于表2 中。关于算法的计算量问题,本文只统计乘除法的运算次数,不统计加减法。从表2中可以看出,标准卡尔曼滤波算法的计算量主要集中在G(n)、P(n)和K(n+1,n)上,相比之下,和α(n)的计算量可以忽略不计,所以要想减少计算量,需从G(n)、P(n)和K(n+1,n)入手。

表2 标准卡尔曼滤波算法的计算量
2 改进的卡尔曼滤波解卷积算法
仔细研究标准卡尔曼滤波解卷积算法发现,G(n)、P(n)和K(n+1,n)三者的迭代计算在极短的时间内即可达到收敛,并且G(n)只与H(n)有关,与观测信号无关;而α(n)、除与H(n)有关外,还与当前时刻的观测信号X(n)有关。对于非时变系统而言,G(n)一旦收敛,就不再变化,因此可以把与G(n)计算有关的项提取出来单独计算,待其收敛后再进行α(n)和的计算,从而实现解卷积。因此,可以通过把标准卡尔曼滤波解卷积算法分解成两个子循环的办法来到达降低样本平均计算量的目的。新算法的迭代步骤列于表3 中。

表3 改进的卡尔曼滤波解卷积算法
通过改变标准算法的迭代次数和迭代顺序,使其在保证稳定性的同时,又能明显减少计算量。在卡尔曼增益G(n)的计算中,Bg的选取要具体问题具体分析(例如,若算法要求计算量小,则Bg尽量小;若算法要求收敛性,则Bg可以大一些)。该算法通过牺牲收敛速度来降低算法的计算量,但牺牲的收敛速度有限。
在分块解卷积算法中,认为在一个块内系统冲激响应是不变的,假设一个解卷积块的长度为B,则从上述迭代过程中可以看出,改进算法比标准算法减少的计算量为(B-Bg)(4L3+4L2N+2LN2+N3)。
3 仿真实验
在仿真实验中用到的数据是实测的房间冲激响应(信道数N为4,长度为1300 点)和一段语音信号(长度为21000 点)。把已知的语音信号作为声源信号s(n),然后将声源信号与实测的房间冲激响应卷积(在不同的仿真实验中,房间冲激响应的长度会有多不同)来获得卷积信号。由于本文只讨论算法计算量的问题,所以在仿真实验中不加入噪声。
令解卷积信号估计误差e(n)=se(n)-s(n)的均方值为E(n);声源信号的均方值为Q(n)。采用如下的滑动平均公式在线估计:
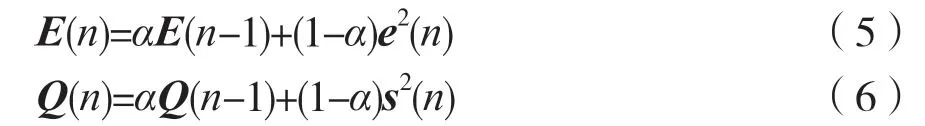
其中,滑动因子α=0.9;n是迭代次数;e(n)为算法输出误差;se(n)为算法的解卷积信号;s(n)为声源信号。
定义解卷积信号的误差-信号比作为评价算法性能的标准:
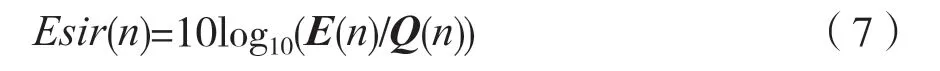
Esir曲线能够反映出算法的收敛水平,单位是分贝(dB)。
3.1 卡尔曼增益的收敛速度
在第2 节中提到,对于非时变系统而言,G(n)一旦收敛,就不再变化,而卡尔曼增益G(n)的计算只与房间冲激响应H(n)有关,所以本节的仿真内容是确定卡尔曼增益的收敛速度。在本节中房间冲激响应的长度分别取L=100,150,200(从已知的房间冲激响应中任意截取)。标准卡尔曼滤波算法中对于不同长度的房间冲激响应时卡尔曼增益的收敛情况见图1。由于卡尔曼增益在全局的收敛速度较快,所以图1 中的卡尔曼增益的收敛情况为前400点的放大图。从图1 中可以看出,卡尔曼增益的收敛速度几乎与房间冲激响应的长度L相同。
3.2 改进的卡尔曼滤波算法对解卷积结果的影响
在本节的仿真实验中,房间冲激响应长度L=150,在上一节的仿真实验中发现卡尔曼增益的收敛速度几乎与房间冲激响应的长度L相同,所以本节中选取改进算法的卡尔曼增益的迭代次数Bg=L+10=160。图2(a)给出了仿真卷积信号(1)声源信号(2)改进算法的解卷积信号(3)和标准算法的解卷积信号(4)的波形比较。其中仿真卷积信号是第2 路的卷积信号。从图2 中可以看出两种算法都有较好的解卷积效果,改进算法只是收敛速度慢一点,一旦收敛,二者的解卷积结果一致。
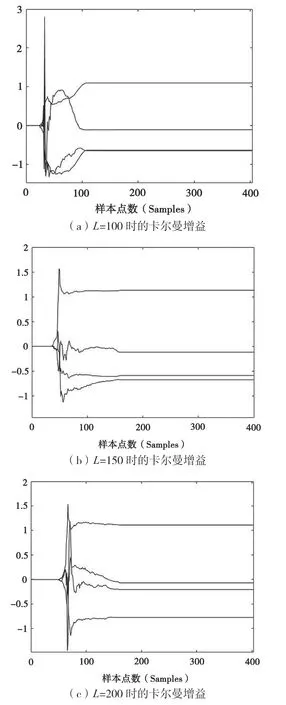
图1 不同长度的房间冲激响应对应的卡尔曼增益的收敛情况(L=100,150,200)
图2 声源信号、卷积信号和两种算法的解卷积信号的比较
3.3 改进的卡尔曼滤波算法对收敛速度的影响
本节与上一节实验相同,房间冲激响应长度L=150,B=5L=750,Bg=L+10=160。利用两种算法的解卷积信号来绘制出Esir 曲线,如图3 所示。
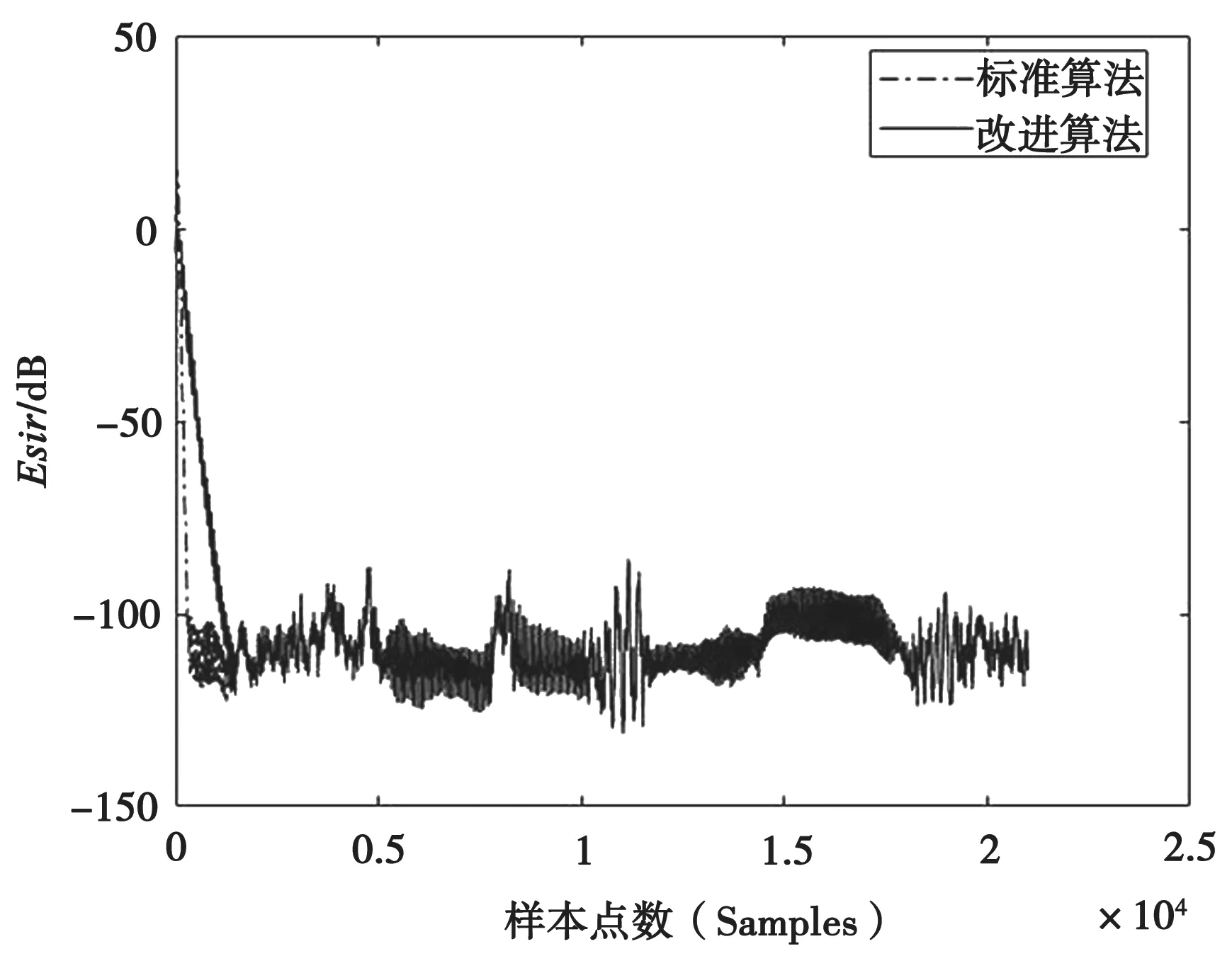
图3 标准算法解卷积信号和改进算法解卷积信号的Esir 曲线
从图3 可以看出,虽然改进算法的解卷积信号没有标准算法解卷积信号那么高的信噪比,但是改进算法的解卷积信号的Esir 也能够快速达到50dB以下。从算法的运行时间来看,在仿真实验所用的计算机上,本节实验的标准算法的运行时间是5.92秒,改进算法的运行时间是1.56 秒,减少了73.6%的运行时间,说明计算量减少了70%以上。
4 结语
本文提出了一种基于卡尔曼滤波解卷积的优化算法,利用卡尔曼增益在短时间内收敛的特点,将标准卡尔曼滤波算法用两个子循环来完成,卡尔曼增益、状态矢量一步预测误差的自相关矩阵和状态估计误差的自相关矩阵的迭代作为一个子循环,状态矢量和新息的迭代作为一个子循环。在仿真实验中可以看出,与标准卡尔曼滤波解卷积算法相比,本文提出的改进算法牺牲的收敛速度有限,但降低的计算量是明显的。

