基于麦克纳姆轮的AGV 定位及纠偏技术的研究
王殿卫,郭津津,李维骁
(1.天津理工大学机械工程学院天津市先进机电系统设计与智能控制重点实验室,天津300384;2.南京邮电大学通信与信息工程学院,南京210023)
自动导航运输车(AutomatedGuidedVehicle,AGV)是现代生产中的重要装备,定位精度以及导航精度是制约其发展的重要因素.现使用的导航方式主要有磁导引、激光导航、惯性导航以及二维码导航,但是磁导航、电磁导航柔性差[1,2],激光导航容易受到环境光线的影响[3],惯性导航会产生误差累积[4].于是快速响应(Quick Response,QR)二维码导航产生,其由惯性导航加上在特定位置纠偏组成[5],其吸收了惯性导航实时性好的优点.又在站点处对误差进行纠正,所以其效果较好,而站点处的纠偏算法为其难点.
Gupta N、陈宁等使用纯追踪(Pure Pursuit)算法,或其改进算法[6,7],能很好的跟踪航向角与转向角,但其误差较大,适用于农机等对误差要求不高的领域.郭景华等人采用遗传算法控制[8],但需要大量训练且实时性不高.杨前明等人使用PID 算法来纠偏[9],获得良好的效果,但是PID 算法快速性与稳定性取决于三个参数的确定,对干扰等不敏感.H.Q.T.NGO[10]等人采用模糊算法控制小车寻迹,但实时性不高.而将模糊控制和PID 算法结合的模糊自适应PID 算法,可以达到更好的效果.其使用模糊算法计算出实时变化的PID 参数,再使用PID 算法计算出小车四个电机的转速,从而对小车行进方向进行控制.
而转向轮主要有单舵轮式[11]、差动式[12]、以及万向轮式.万向轮主要有连续切换轮[13]以及麦克纳姆轮(Mecanum)轮[14].
本AGV 系统采用麦克纳姆轮(以下简称麦轮)作为驱动轮,并采用二维码导航,模糊自适应PID 算法于站点处纠偏.
1 麦轮运动分析
1.1 麦轮简介
麦轮是一种全向轮,如图1.其圆周分布一些可以自由转动的梭状的辊子,辊子与轮截面成45°. 由于四轮转速各不相同,所以地面对四个轮的反作用力方向以及大小都不相同,因此四个力的合力可根据四轮转速变化而变化,再加上辊子的辅助,使得AGV 可以在平面内做前后、左右以及以绕中心旋转三个自由度的运动[15].

图1 麦轮实物图Fig.1 Mecanum wheel
1.2 麦轮运动模型
如图2 所示,中点O 为相对轮两两连线的交点,轮子中间两条斜线代表轮子上的辊子方向. ω→为AGV 角速度矢量分别为小车x轴、y轴运动向量为0 号轮相对于世界坐标系的速度矢量,不代表实际速度.
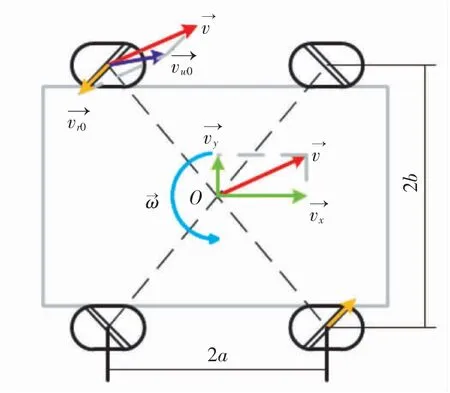
图2 AGV 车体速度模型Fig.2 Velocity model of body of AGV
由图可知:

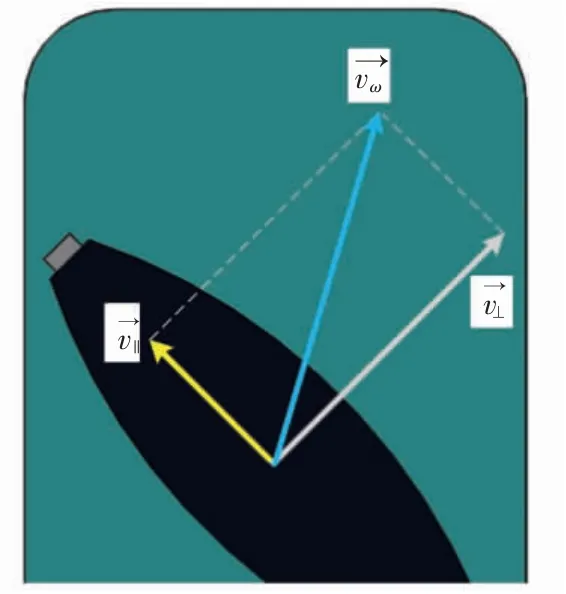
图3 单个辊子速度Fig.3 Velocity model of single roller
由图可知:

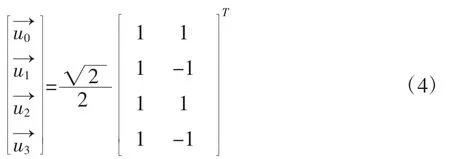
车轮转速与辊子的速度有如下关系
其中,ωi为i轮转速;R为麦轮半径.
综上所述麦轮逆运动学公式为
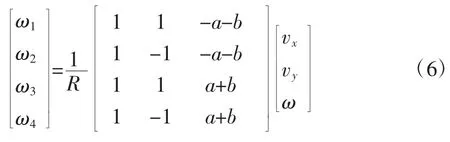
2 QR 码定位
QR 码有两个作用.首先,QR 码用于确定直线误差与角度误差.当扫描到QR 码时,AGV 会通过三个角点找到QR 码中心点以及QR 码的方向,并计算出横向偏差以及角度偏差.其次,QR 用于确定其世界坐标,AGV 会将QR 码解析成代表坐标的数字,并根据其坐标选择行进方向.解析二维码使用开源函数库Zbar[16],但是Zbar 需要接收优质的二进制图像,所以需要对图像进行预处理.为提高实时性,图像处理过程采用了Opencv 和C++进行开发.
2.1 图像预处理
未经处理的图像为RGB 图像,处理速度慢,因此首先需要将图像转化为灰度图像.由于电子干扰等原因,图像会出现噪声,一般为椒盐噪声,中值滤波可以很好地将噪音滤除[17].
QR 二维码为黑白两种颜色组成,因此可以将图像转化为二值图像,如此可以在不损害信息的情况下增加运算速度.图像二值化通过阈值处理实现,即灰度值大于阈值的置为1,反之则置为0. 阈值的确定有全局阈值算法以及局部二值化算法.全局阈值算法最经典的方法为Otsu(大津算法). 其通过求取图像灰度直方图双峰之间的低谷值来确定阈值[18].因此,适用于前景与背景对明显的图像.但由于QR 码被粘贴在地板上,光源为自然光,加之AGV 车体对光线的遮挡,会出现光照不均的现象,因此Otsu 算法并不适用.如图4 所示.

图4 Ostu 算法Fig.4 Ostu algorithm
对于光照不均的图像,局部二值化算法较为适用,常用的局部二值化算法有Niblack 算法以及Wellner算法.但Niblack 算法计算量较大,不适合实时性要求较高的嵌入式系统.图5 为经过Niblack 算法计算结果.

图5 Niblack 算法Fig.5 Niblack algorithm
Wellner 算法原理[20]为,以“S”型曲线(如图6)遍历整个图像,并将其灰度值存入一维数组中.

图6 Wellner 算法遍历顺序Fig.6 Traversal sequence of Wellner algorithm
再取需求阈值的像素点n之前的s个数(包含n点),求其平均值.经验表明一般取s=w/8.w为一行的像素数.为体现和第n点间距离对结果的影响,则求取其加权平均值,如下所示:

为关联竖直方向的像素值,用下式得数hs(n)代替gs(n)
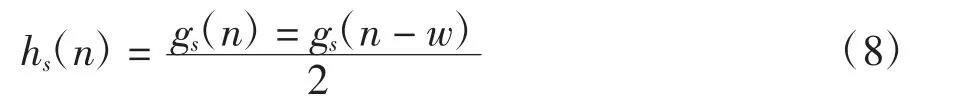
最终二值化公式为:
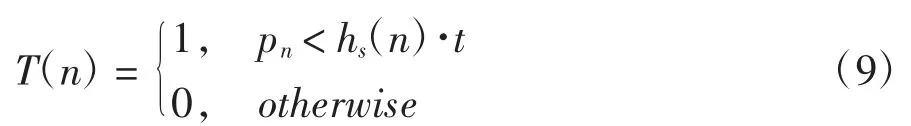
其中t为修正系数,经验得t=0.85 效果最佳,其结果如图7,其中形态学操作使用5×5 的矩形模板.

图7 Wellner 算法Fig.7 Wellner algorithm
由图7 可知Wellner 算法比Niblack 算法效果要差,图7(d)中间偏左下位置有瑕疵,但可正常解码,在嵌入式环境下Niblack 算法运行时间为138 ms,解码成功率为98.4%,Wellner 算法运行时间只有16 ms,成功率为95.6%.
2.2 QR 码中心以及方向定位
本小节中的坐标均基于像素坐标系.
QR 码角点(又称位置探测图形)位于QR 码的左上、左下、右上三角上,可根据其位置计算出QR二维码的中心.
可寻找到三个角点后并提取其外轮廓,后求其一阶空间矩[21],即求出角点的中心坐标,其公式见式(10),然后根据三个角点的几何关系找到二维码中心及方向,如图8 所示,其中向量的方向为QR码的方向.

其中,m为x轴坐标值;n为y轴坐标值;m00为图像的零阶空间矩;m10为x方向的一阶空间矩;m01为y方向上的一阶空间矩;为中点x坐标值;为中点y坐标值.
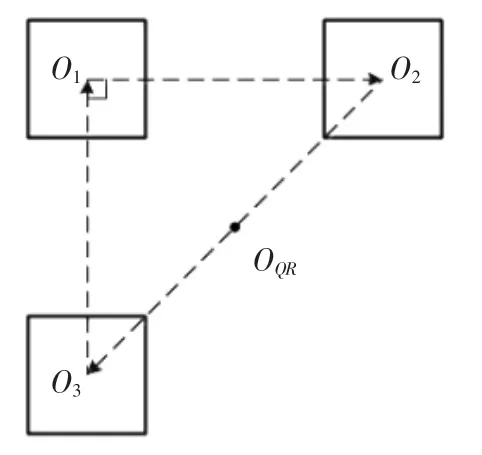
图8 三个角点相对位置Fig.8 The location of three corner areas
3 纠偏算法研究
3.1 模糊PID 算法简介
PID 算法是按偏差的比例(P)、积分(I)和微分(D)进行运算的算法[22].增量式PID 表达式如下,其原理简单应用面广,被广泛应用. 其难点为对参数Kd、Ki、Kp的确定.
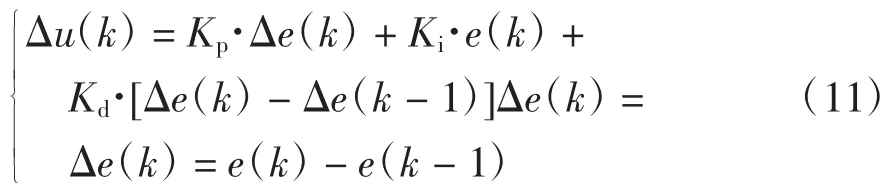
其中,Δu(k)为k时刻输出的补偿量,Kp、Ki、Kd分别为PID 的比例、积分、微分参数,e(k)为k时刻实际值与设定值的差值.
模糊算法是一种智能控制算法,其以模糊集合论、模糊语言变量和模糊逻辑推理为基础[23],适用于难以建立系统模型的情况.
模糊自整定PID 将模糊算法与PID 算法结合,使用模糊算法实时计算出Kp、Ki、Kd参数,可以较好继承两种算法的优点.
3.2 控制策略描述
在站点处有横向偏差e与角度偏差θ 两种偏差,因此,需要设计两个不同的模糊自整定PID 控制器,分别来控制两个误差以达到精准控制的目的.控制流程如图9.
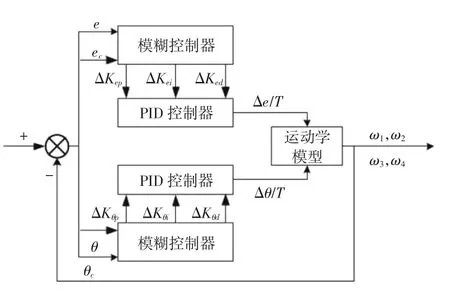
图9 控制流程Fig.9 Control flow
3.3 模糊化处理
模糊控制器需输入模糊信号,因此首先要对两个偏差e、θ、偏差变化率ec、θc以及输出量Kp、Ki、Kd进行模糊化处理.其中e的基本论域与摄像头的摄像范围有关,取最大偏差为40 mm,因此e的基本论域范围为[-40,40]mm.偏差变化率ec与AGV 的横向移动速度有关,取ec论域为[-10,10]mm/s.取θ 论域为[-π/4,π/4],θc为[-π/16,π/16].
设定所有的输入量在模糊集上的论域都均为[-3,3],即论域{NB,NM,NS,ZO,PS,PM,PB},其分别表示为负大、负中、负小、零、正小、正中、正大.因此各个量的量化因子[24]为

同理根据经验可知输出量的论域为:

量化因子为:

隶属度函数均采用三角形函数如图10.
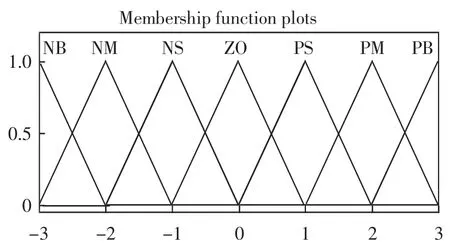
图10 隶属度函数Fig.10 Membership function
3.4 模糊推理
模糊推理即是使用模糊输入量通过和模糊规则库进行对比得出最优的输出值,根据PID 三个参数的特性[25]得出规则表如表1,θ、θc——ΔKp、ΔKi、ΔKd的规则表与表1 相同.
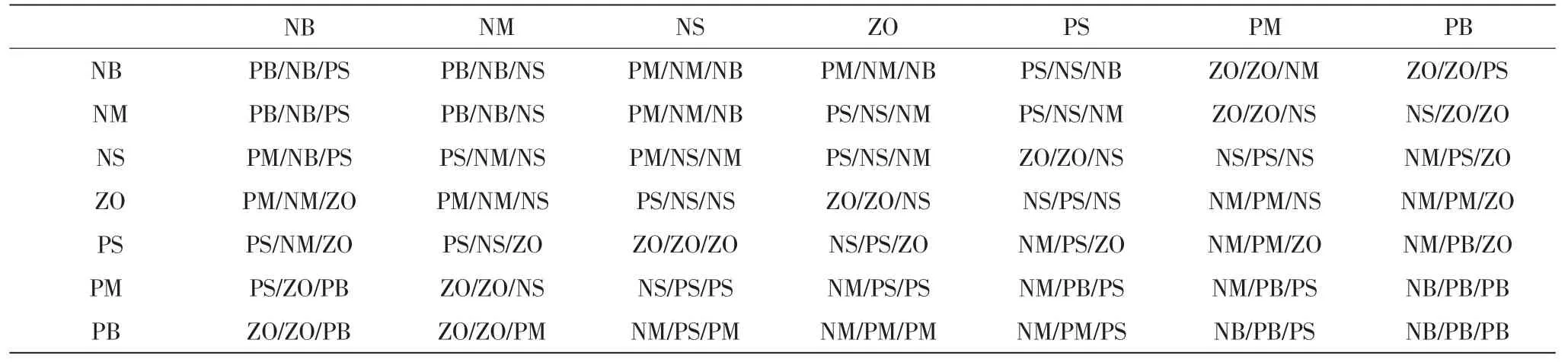
表1 e/ec——ΔKp、ΔKi、ΔKd 规则表Tab.1 Rule table of e/ec to ΔKp/ΔKi/ΔKd
3.5 解模糊
经过模糊推理后,输出的仍然是模糊值,无法在嵌入式平台上运行,需要将其解模糊化.解模糊化算法使用加权平均值法[26],其公式如下:
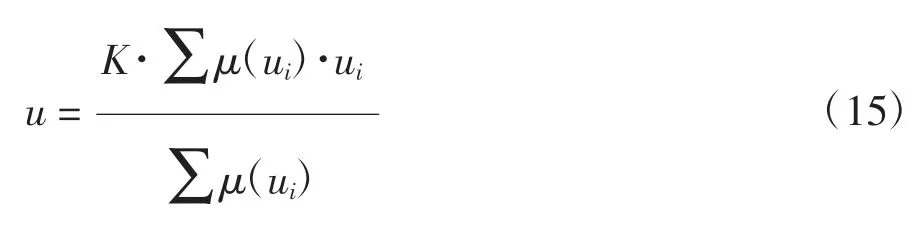
其中,u为解模糊化之后的精确量;K为其对应的量化因子;ui为第i个元素;μ(ui)为其对应的隶属度函数值.经过解模糊化后即可将其作用在被控对象上.
4 实验验证
为验证算法可靠性,特设计实验. 实验分为两组,第一组直线行驶实验,AGV 分别以前进与平移的方式运动,速度设置为0.3 m/s,站点之间距离为3 m,共设有5 个站点,其实验结果平均值如表2.
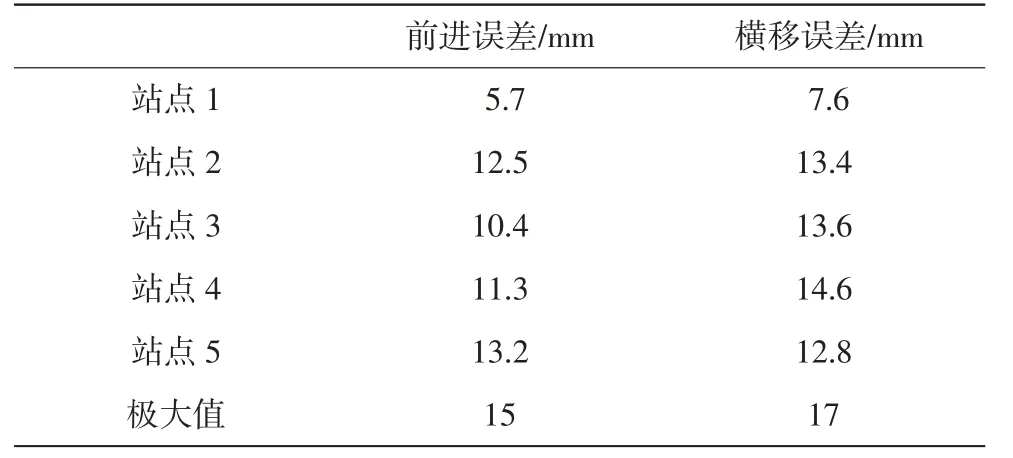
表2 前进/横移实验结果Tab.2 Result of experiment of forward and lateral motion
第二组实验为AGV 受到扰动时设计,实验方法为将AGV 与设定轨迹成一定角度放置,测算其恢复直行时间,其实验结果平均值如表3.
由上两组实验可知,前进与横移过程中误差最大不超过20 mm,误差符合实际工况下精度要求.而抗扰动实验中,在与实际轨迹成55 度时,AGV 会脱离轨道,较小角度下,调整速率较快.大多数情况下,角度误差不会超过30°,所以可以符合要求.
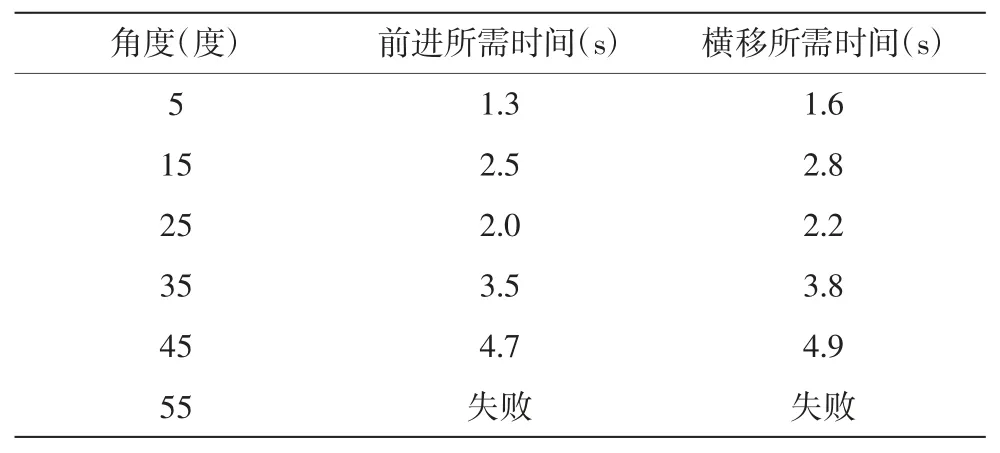
表3 抗扰动实验Tab.3 Result of experiment of tamper-proof
5 结 论
本文设计了一款基于麦克纳姆轮以及QR 码定位的AGV,首先分析了麦克纳姆轮的运动学模型,而后分析了其定位所需的图像处理算法以及出现误差时纠正算法,实验结果显示其运转状态良好,出现偏差纠正速度较快,但仍有以下不足:
1)未设计转弯算法.
2)受到干扰调整时间还可以降低.
3)为满足特定需求,角度调整仍需扩大.

