HSS模型在海口地区超大型深基坑中的应用研究

陈 源，潘宇雄，胡会根，谢群政

（海南有色工程勘察设计院 海口570206）

0 引言

大量的工程现场测试结果表明，在施工过程中基础、基坑、隧道等地下结构周围的相当一部分土体，在工作荷载状态下仍处于10-4～10-3之间的小应变状态，在小应变条件下土体真实刚度值明显要比从常规试验得到的名义弹性刚度值高很多［1］。Benz［2］在土体硬化模型HS（Hardening soil model）的基础上考虑了小应变阶段时土体刚度增加的特性，进一步修正和发展提出了小应变硬化土模型HSS（Hardening soil model with small strain stiffness），该模型不但能同时考虑压缩硬化和剪切硬化，且还可以考虑加卸载以及剪切刚度在小应变量级范围内随应变衰减等行为。此外HSS 模型参数比较直观，可以由现场原位测试和实验室测得，因此该模型更适合模拟基坑开挖问题，模拟结果和实测结果更吻合。管飞［3］将HSS 模型应用在软土超大型深基坑的3D数值分析中，褚峰等人［4］对土体小应变条件下紧邻地铁枢纽的超深基坑变形特性进行了数值分析，尹骥［5］将HSS 模型应用在上海地区深基坑工程中，数值分析结果和工程实际吻合都较好，对工程设计和施工具有重要价值。

岩土参数的正确合理获取是保证数值分析可靠性的非常重要极其关键的一步。王卫东等人［6］对上海地区基坑开挖数值分析中土体HSS 模型参数进行了研究，获取了上海地区典型土层模型参数并验证了其适用性。本文基于岩土工程数值分析软件Plaxis，选用HSS 模型进行数值分析，通过原位测试、室内实验、经验公式、已有研究成果等手段，综合确定给出了一套适用于海口地区典型地层的HSS 模型参数选用建议方法，并将其应用在实际基坑工程中，研究分析该模型在当地的适用性和可靠性。通过将数值模拟结果与实际监测结果进行对比，研究分析二者的吻合度，反过来也验证HSS 模型在研究地区的适用性和参数选用建议方法的合理性和可靠性。

1 HSS模型简介

1.1 HS模型

HS 模型的基本思想源于三轴加载下竖向应变ε1和偏应力q 之间的双曲线关系，图1 给出了这种关系的曲线:

式中:Ei为初始刚度；qa为抗剪强度的渐进值:qf为极限偏应力，具体定义如下:

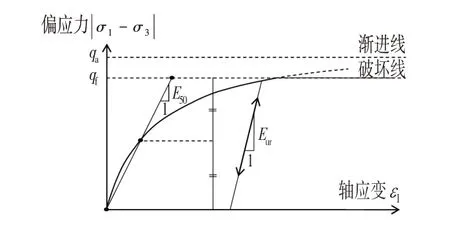
图1 标准排水三轴试验主加载下双曲型应力-应变关系曲线Fig.1 Hyperbolic Stress-Strain Curve under Main Load in Standard Drained Triaxial Test

式中:Rf为破坏比；c为粘聚力；φ 为内摩擦角。

HS模型考虑了相应的塑性应变，屈服函数为:

HS 模型采用流动法规则，其塑性应变率（剪胀性）的关系为:

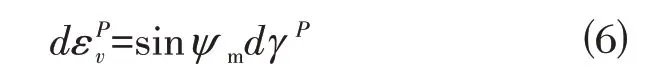
式中:ψm为动剪胀角。

HS模型考虑了三轴加载刚度E50和三轴卸载刚度Eur的差异性:

HS模型引入了1个屈服帽盖，如图2所示。

图2 HS模型的屈服帽盖Fig.2 Yield Cap of HS Model

1.2 HSS模型

HSS 模型是基于HS 模型而建立的，两者有着几乎相同的参数。HSS模型中只增加了2个参数用于描述小应变刚度行为:

⑴初始小应变模量G0；

⑵ 剪切应变水平γ0.7，即割线模量Gs减小到70%G0时的应变水平。

G0和γ0.7主要受材料应力状态和孔隙比e的影响。G0的表达式为:

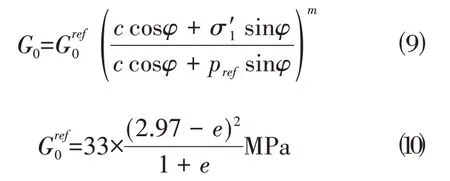
γ0.7的近似表达式为:

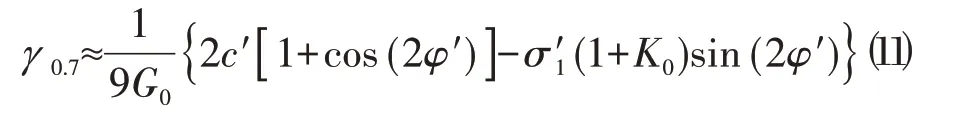
式中:c'为有效粘聚力；φ'为有效内摩擦角；K0为静止侧压力系数。

2 参数的确定

2.1 工程地质概况

海口市位于海南省最北部，靠近海边及中心城区地区上部大都是第四系中更新统、下更新统海相或海陆相沉积土层，下部为第三系上新统海相沉积土层；中部及南部上部为火山岩地层，中下部均为海相沉积地层。海口国兴大道地区主要地层为第①层粉质粘土（Q2mc），第②层中砂（Q2mc），第③层粘土（Q1m），第④层粗砂（Q1m），第⑤层粉质粘土（Q1m），第⑥层粉砂（Q1m），第⑦层粘土（Q1m），第⑧层粉质粘土（N2m）。

2.2 参数的确定

地质情况具有区域性和相似性，通过原位测试和室内实验获得相关基本参数，结合经验公式和已有研究成果分析获得了海口地区典型地层的HSS模型参数。

图3 固结应力应变曲线确定Fig.3 Determination of According to Consolidation Stress-Strain Curve

图4 三轴CD实验应力应变曲线确定Fig.4 Determination of According to Stress-Strain Curve of Triaxial CD Experiment

图5 三轴CD实验应力应变曲线确定Fig.5 Determination of According to Stress-Strain Curve of Triaxial CD Experiment

3 工程概况

3.1 工程项目简介

工程位于海口市国兴大道与五指山南路交叉路口东北侧。基坑呈矩形，总面积约14.8 万m2，周长约1 600 m，开挖深度11.5～17.5 m，为超大型深基坑，基坑支护平面布置如图6所示。

表1 HSS模型参数选用Tab.1 HSS Model Parameter Selection

基坑采用土钉墙+φ 1 200钻孔灌注桩+桩后φ 800三重管旋喷止水桩+3 道预应力锚索的支护形式，图7为B区南侧支护剖面。

图6 基坑平面Fig.6 Foundation Pit Plan

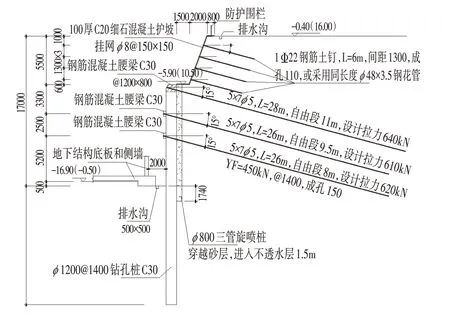
图7 基坑剖面Fig.7 Section of Foundation Pit

3.2 场地工程地质水文地质条件

场地土层及物理力学参数如表2 所示，地下水为第②层中砂、第④层粗砂中的孔隙潜水、第⑥层粉砂中的孔隙微承压水，潜水稳定水位埋深为3.50～11.00 m。

表2 海口地区典型地层HSS模型参数Tab.2 HSS Model Parameters of Typical Strata in Haikou Area

4 数值模拟

4.1 几何模型及边界条件

数值分析采用Plaxis 有限元软件，该软件率先引入了HSS模型。

基坑沿长宽度方向几乎对称，因此在数值计算时取1/2基坑宽度的模型进行分析。模型区域为230 m×100 m，基坑开挖边线距模型边界线100 m（大于5 倍基坑开挖深度），模型高100 m（大于5 倍基坑开挖深度），基本可以消除边界影响。设定初始应力状态，分部施工模式为实际施工工况顺序。模型边界条件为固定约束，不透水边界，降水和开挖逐步进行，坑外侧水位始终保持在地面下3.5 m 不变，坑内水位始终保持在当前开挖面以下1.0 m 左右。有限元计算模型如图8所示。

图8 有限元计算模型Fig.8 Finite Element Calculation Model

4.2 数值模拟结果

HSS 模型模拟的结果:坑外地表表现为沉降，最大位移在坡顶，影响范围大概为1倍基坑深度；坡顶水平位移最大，桩顶次之，支护桩结构外侧土体和内侧土体都有较明显水平位移；坑底竖向位移表现为回弹拱起，在支护桩附近位置较明显，这要比其它模型更符合工程实际。由于HSS 模型考虑了卸载再加载情况并且引入了小应变参数，所以更适合分析对周边环境敏感的基坑工程。水平位移云图如图9 所示，竖向位移云图如图10所示。

4.3 结果分析

坑外地表沉降是一个很重要的指标，坑外可能会有重要建筑物、市政道路、市政管线等，对基坑进行数值模拟和实时监测，保证基坑安全的同时也要保证周边环境的安全。有较大嵌固深度的支护结构或支护结构底入土在刚性较大的土层内时，地表沉降通常呈凹槽形，沉降的极大值不在支护结构旁，而是位于距支护结构一定距离的位置［9］。模拟曲线与实测曲线走势基本一致，模拟计算坡顶最大沉降为27.2 mm，理正深基坑软件理论计算最大值为25.5 mm，基坑监测坡顶最大沉降为24.3 mm，模拟数值比实测值稍大，沉降极大值位置基本一致，与工程实际现象基本一致。坑外沉降实测值与模拟值如图11所示。

图9 水平位移云图Fig.9 Horizontal Displacement Nephogram

图10 竖向位移云图Fig.10 Vertical Displacement Nephogram

图11 坑外沉降实测值与模拟值Fig.11 Measured and Simulated Values of Settlement outside The Pit

根据实测测斜数据，最大位移不在桩顶，而在桩顶下桩身某个位置，支护结构腹部向基坑内突出，表现为抛物线形，符合徐杨青［10］的研究成果。模拟桩身变形为抛物线形，模拟计算最大水平位移为30.8 mm，理正计算最大值28.4 mm，基坑监测最大值26.8 mm。模拟曲线与实测曲线走势基本一致，模拟数值比实测值稍大，水平位移极大值位置基本一致，模拟效果较理想。支护桩位移实测值与模拟值如图12所示。

5 结论

HSS 模型是能较全面地反映土体变形特性的一个本构模型，参数比较直观且物理意义明确，模型考虑了小应变特性，用于超大型深基坑的数值分析是可行的，特别适合用于对周边环境较敏感的基坑工程的高级数值分析，对过于保守的工程设计和施工技术措施能进行合理的优化。

图12 支护桩位移实测值与模拟值Fig.12 Measured and Simulated Displacement of Supporting Pile

通过对海口地区典型的土层进行原位测试和室内土工实验，总结了一套适用于海口地区典型土层的HSS 模型的参数取值方法，同时也给出了相应的建议值。采用建议的参数取值对超大深基坑进行了数值模拟，与实测结果吻合得较好，说明本文采用的数值分析方法具有合理性和适用性，也验证了建议参数取值方法的适用性和可靠性，为以后的建模计算提供参考。