框架结构振动放大效应模型试验研究

张一帆，周传波，吴廷尧

（1、广东省工程勘察院 广州510510；2、中国地质大学（武汉）工程学院 武汉430074）

0 引言

随着现代工程建设的发展，在既有框架结构建筑物周边，出现越来越多需要进行基坑、边坡、隧道等岩石爆破开挖的情况，同时自然地震对建筑结构的影响规律也一直深受科研人员的关注。研究分析建筑框架结构在振动波作用下产生的振动放大效应，可以为爆破震动控制和结构抗震设计提供依据。

目前对于振动作用下框架结构的响应特征分析的研究方法主要包括:通过理论数学模型计算进行的理论分析；通过数值模拟软件进行的三维有限元分析；采用物理模型试验进行的实物模拟分析。对于低频地震波的模拟目前比较完善，如李国强、周娜等人通过振动台试验和数值模拟的方法，模拟地震波对钢-混结构的影响，通过输入不同的地震波分析结构各层的加速度、位移的变化，并对模型的破坏特征进行了分析［1-4］。由于目前没有理想的模拟爆破振动波的实验仪器，高频的爆破振动波对建筑物的影响方面的研究主要为王俊平、曹建良等人通过数值模拟的方法，探讨了几种不同建筑体系的爆破振动响应特点［5，6］。

本文采用振动台模型实物试验的方法对研究目标进行分析，首先根据相似理论对6 层框架结构进行了1/20 缩尺实物模型的制作，然后通过振动台试验，得到在水平、垂直方向振动作用下，不同加载强度和不同加载频率下框架模型加速度的放大效应。

1 模型试验的相似性

1.1 相似理论

模型试验的基础是相似理论，在模型试验中，结构尺度的缩小或放大，加载参数的提高或降低，模型边界条件的确定等都是在相似理论的基础上进行的。进行振动台结构模型试验时，首先把原型结构按照一定的比例尺进行缩尺模型制作，在制作好的模型上进行各种试验前，还要根据边界相似条件确定结构的固定形式，根据加速度、频率、时间等相似比，把作用在原型结构上的荷载，转换成相应的作用在模型结构上的荷载，在这些条件的基础上进行模型试验得到的试验数据和结果，又可以根据相似关系反推到原型中去，从而运用于实际工程项目。

1.2 模型材料的选取

选择合理的相似材料是进行模型试验的先决条件，其不仅关系到能否反映出研究目标原型结构的特性，还关系到模型结构制作的难易程度及试验的进展快慢。

本次模型试验以一栋6层的单跨钢筋混凝土框架建筑为原型结构，综合考虑了本次试验振动台的尺寸、负载能力及实验室条件的基础上，确定模型结构与原型结构的几何相似常数为1/20，试验实物模型与原型结构概况如表1所示。

表1 模型与原型概况Tab.1 The Overview of Model and Prototype

根据相似理论，制作模型所采用的相似材料的物理力学参数，必须与原型材料的物理力学参数满足理论计算的相似比。对于混凝土的模拟当前一般采用微混凝土［7，8］，在本实验中由于几何相似比较小，微混凝土制作成型较复杂且养护时间较长，而石膏的弹模、泊松比等参数满足本实验要求，并且易于加工、凝固时间短，故本实验采用石膏模拟混凝土，采用镀锌铁丝作为结构中钢筋的模拟。

1.3 物理相似常数的确定

本文采用量纲分析法确定模型试验的相似常数，即先确定几个基本相似常数，然后通过数学公式量纲推导，以获得其它所需的相似常数［9］。依据框架结构模型试验理论及经验，首先确定的基本量纲为SL（几何相似常数）、SE（弹模相似常数）、Sρ（密度相似常数）。对所选取的不同水膏比的石膏试样进行单轴抗压试验，以获得试验试样的干容重、抗压强度、弹性模量和泊松比等所需的物理力学参数，如图1及表2所示。

图1 单轴抗压实验Fig.1 Uniaxial Compression Experimen

通过上述试验计算得到的物理力学参数，并综合考虑试验模型成型的难易程度，确定相似石膏材料的水膏比为0.8∶1。对于振动台试验等动力模型试验，除需满足基本量纲关系外，还需满足式⑴要求:

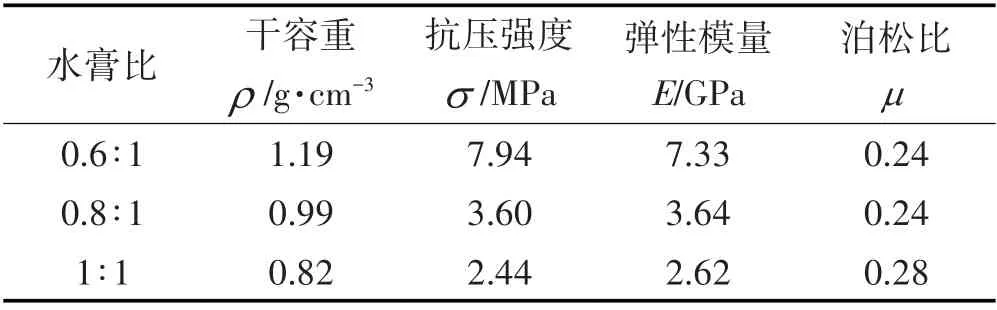
表2 不同水膏比单轴抗压测试结果Tab.2 Test Results of Uniaxial Compression Experimen

即试验采用的SL（几何相似常数）、SE（弹模相似常数）、Sρ（密度相似常数）、Sg（重力加速度相似常数）必须满足上述公式的要求。Sg考虑到本次的试验条件Sg=1，得到式⑵:

可以看出，模型的几何尺寸一般小于实际尺寸，SL一般小于1，为满足上述公式需要模型材料的弹性模量小于原型材料的弹性模量或者模型材料的密度大于原型材料的密度，这在实际模型材料选择中是十分困难的，为了解决这一问题本次模型试验采用欠人工质量模型的方法，即在模型上增加尽可能多的人工附加质量，以提升模型的整体等效密度来满足试验要求［10］。采用此方法确定的等效密度相似常数计算公式为:

本次振动台试验共在模型结构上增加人工附加质量16.2 kg，基本均匀分布在结构各层。本次模型结构自身质量与附加人工质量之和，也即欠人工质量模型质量达到了完全人工质量模型总质量的74%，避免了忽略重力模型的重大误差［11］。在确定了几何相似系数SL=1/20；弹性模量相似系数SE=3.64/30=1/8.24；等效密度相似系数Sρ=1.8，根据量纲关系推导出其它主要的相似系数如表3所示。

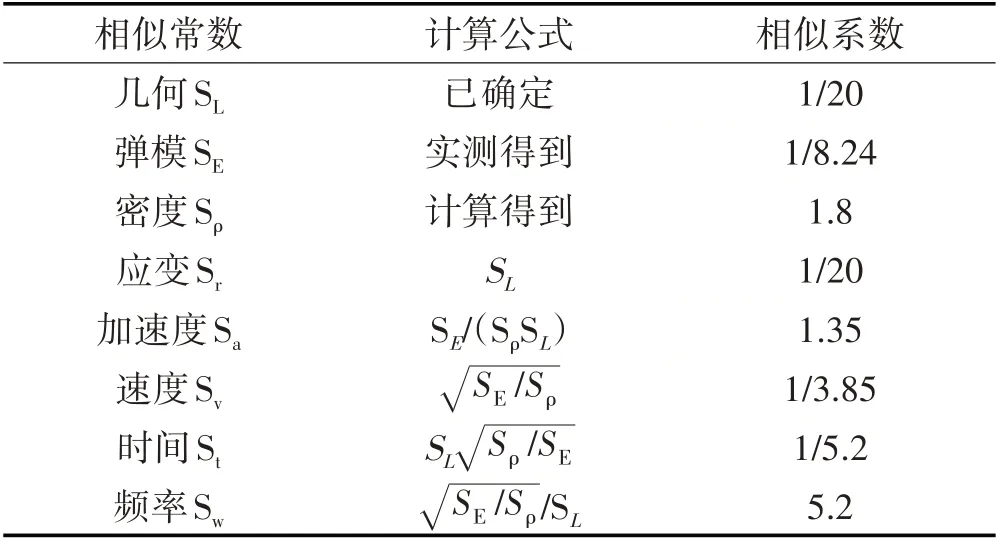
表3 主要相似系数Tab.3 Main Similarity Coefficient

1.4 模型配筋面积的确定

对于钢筋的模拟由于很难找到同时满足几何相似和力学相似的模型材料，这时一般采用抗弯能力等效原则、抗剪能力等效原则进行等效模拟［12］，模型中柱、梁配筋计算公式为:

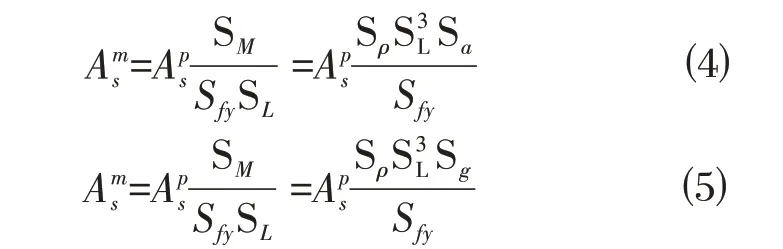
2 模型试验系统与试验方案

2.1 模型制作及模型试验测试系统

实物模型采用薄木板、泡沫材料、石膏、镀锌铁丝等材料逐层浇筑成型，本次试验振动台采用水平-垂直单向液压振动系统，如图2所示，台面尺寸为1 m×2 m，最大速度0.5 m/s，最大负载时的加速度20 m/s2；由于振动台系统自带的数据采集系统通道有限，试验的收集数据系统选用DH5956应变测试仪和各种传感器。

图2 振动台控制系统Fig.2 The Control System of Shaking Table

试验时通过预制好的底板使框架模型与振动台相固定，在每层楼上用加放砖块充当附加质量，根据结构的特点，在底板及2、4、6层顶左、右柱两侧各布置压电式加速度计4 个，共8 个，以获得各测点的加速度值；在底板及3、6 层顶靠近左侧柱的位置布置速度计3 个，以获得各测点的速度值。模型试验实物及各测点布置如图3所示。

2.2 模型试验参数设置

为了简化试验，在振动台上通过加载正弦波来模拟振动波，由于一般地震波的频率约为5 Hz，而爆破振动波频率较高。考虑到试验频率的相似常数和振动台的工作频率范围，三组加载频率分别选取30 Hz、50 Hz、70 Hz。在试验准备阶段发现当加载强度达到0.9g 的时候响应误差较大，故试验选取0.1g、0.3g、0.5g、0.7g 共4 组加载强度参数，分别沿水平、垂直方向共进行24次振动试验，每次试验均持续180 s。

图3 试验实物Fig.3 Test Process

试验过程中通过数控系统控制输入波形的频率、加速度、持续时间等参数。在每次振动试验中通过5 956 应变测试仪收集数据，振动完成后保存实验数据，并对此次的响应误差情况进行记录，确保实验的准确性，若响应误差过大则重复该次试验。通过实验数据及理论知识可知速度的响应特征与加速度基本一致，本次分析以加速度数据分析为主，以速度响应数据作补充验证。

3 试验结果及分析

3.1 结构加速度动力响应分析

对结构加速度动力响应的研究采用最大加速度放大系数进行分析，即模型各层加速度最大值与模型底部输入加速度最大值之比。分析不同加载强度下的加速度放大效应，经过试验数据整理，可以得到不同频率下模型结构表现出的放大规律基本相似。以加载频率为50 Hz时模型结构各层的最大加速度放大系数为例，如图4所示。

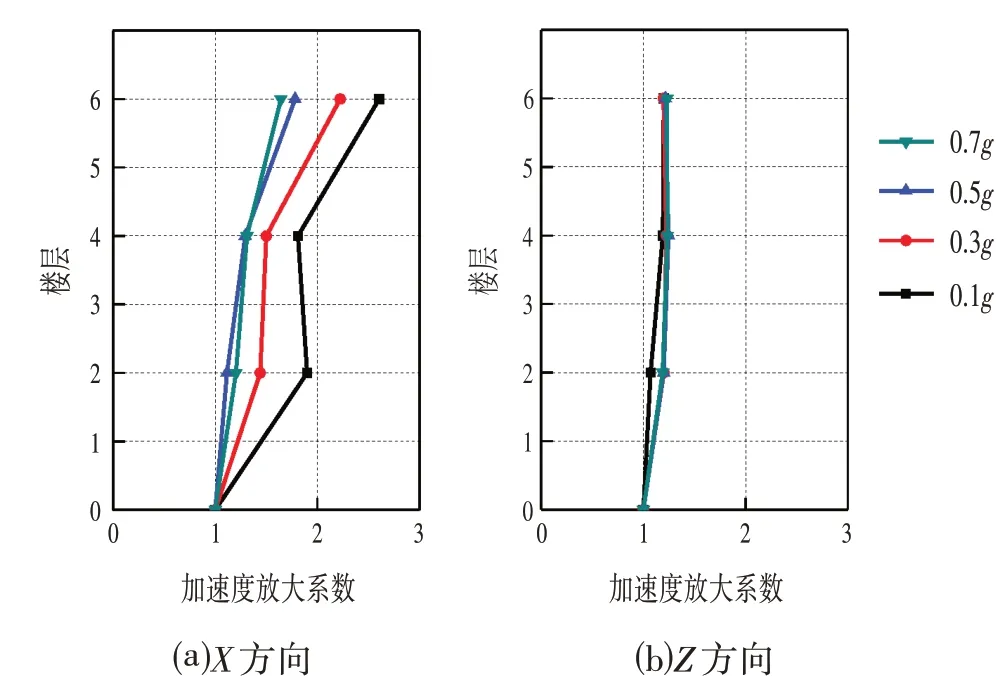
图4 加速度放大系数包络图（50Hz）Fig.4 Acceleration Amplification Factor Envelopes

从加速度放大系数变化情况可以看出，模型框架结构在振动波水平及垂直振动作用下都表现出一定的放大效应，总体上看，楼层越高，加速度放大系数越大，特别是在结构顶层振动放大效应尤为明显。下面对不同加载强度下、不同加载频率下结构的加速度动力响应分别进行分析。

3.2 不同加载强度下结构加速度动力响应分析

由于结构顶层表现出来的振动放大效应尤为明显，通过数据整理及计算得到在不同加载强度下模型顶层的加速度放大系数如表4。

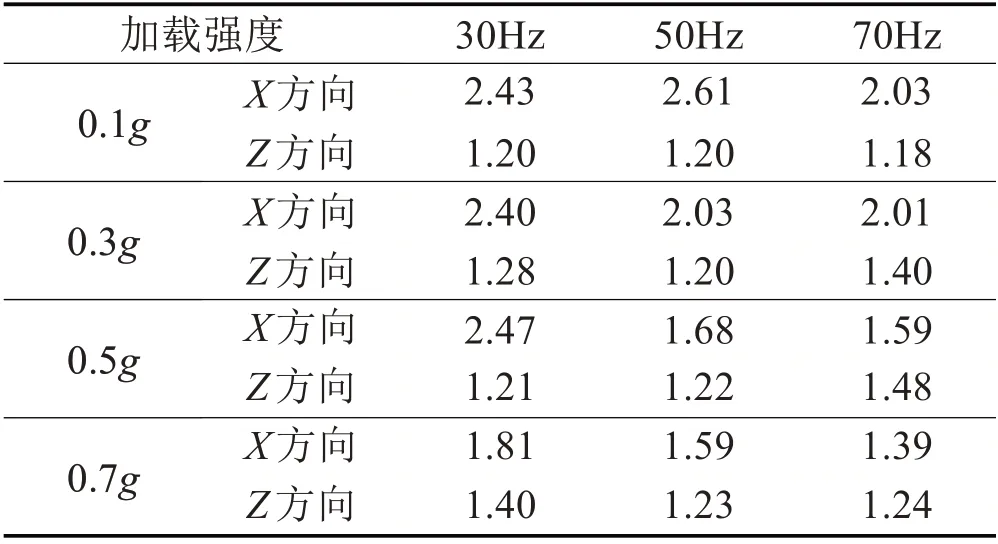
表4 不同加载强度下模型顶层加速度的放大系数Tab.4 The Amplification Coefficient of Acceleration under Fifferent Loading Strength

在加载频率为30 Hz时水平振动作用下结构顶层加速度放大系数集中在1.8～2.5之间；加载频率为50 Hz时水平方向振动作用下顶层加速度放大系数集中在1.5～2.6 之间；加载频率为70 Hz 时水平方向振动作用下顶层加速度放大系数集中在1.4～2.1 之间，并且总体上呈现随着加载强度的增大加速度放大系数减小的规律，分析产生这一规律的可能原因为随着加载强度的增大会导致结构损伤加剧，刚度降低，使模型各层动力放大系数减小。

垂直方向振动作用下放大系数在1.2～1.3 之间基本保持不变，表明竖直振动作用下模型结构各层也会表现出一定的放大效应，但放大系数相比于水平振动作用下较小，可见在竖直振动过程中加载强度的变化对模型各楼层的影响很小。

3.3 不同加载频率下结构加速度动力响应分析

通过实验数据整理得到水平方向振动作用下，在不同加载频率作用下模型结构各楼层的加速度放大系数，分析结构加速度动力响应特征，如图5所示。

可以看出，不同加载频率下模型结构在下部，即2 层的加速度放大系数基本相同，在模型上部，即4～6 层表现出随着加载频率的增大加速度放大系数反而减小的现象，同样这一现象在结构顶层表现得最为明显。考虑到此类模型结构的自振频率一般为5～8 Hz，输入加载的振动波频率越接近结构的自振频率时，模型结构的振动响应会越强烈，表现出的加速度放大系数越大。

结合一般框架结构发生破坏的形式主要为剪切破坏，水平方向的振动是造成结构剪切破坏，产生塑性变形的主要原因，而在垂直振动过程中结构基本不受剪应力的作用，使结构在不同加载频率和强度下具有较好的稳定性。表现为在竖直振动波加载作用下，模型结构各层测得的加速度放大系数基本相同且数值较小。

图5 水平振动作用下加速度放大系数包络线Fig.5 Acceleration Amplification Factor Envelope under Horizontal Vibration

4 结论

本文通过振动台模型试验的方法分析振动作用下框架结构的放大效应，得到以下结论:

⑴本次模型试验选用石膏和镀锌铁丝来模拟混凝土和钢筋，模型制作简单，可行性强，可为其它类似小比例尺框架模型试验研究提供参考。

⑵6 层模型框架结构在振动波水平及垂直振动作用下都表现出放大效应。总体上看，结构上部加速度放大系数大于结构下部，特别是在结构顶层振动放大效应尤为明显，水平振动作用下结构顶层加速度放大系数集中在1.4～2.6 之间，垂直振动作用下加速度放大系数集中在1.2～1.3之间基本保持不变。

⑶水平振动产生的放大效应大于垂直方向振动，结合一般框架结构发生破坏的形式主要为剪切破坏，水平方向的振动是造成结构剪切破坏，产生塑性变形的主要原因，而在垂直振动过程中结构基本不受剪应力的作用，使结构在不同加载频率和强度下具有较好的稳定性。

⑷框架结构的振动响应特征表现为:高强度、低频率的振动波对模型结构的影响较大，表现出的结构放大效应越明显。