面向水声换能器的压电单晶复合材料设计研究
王 婷,李 飞,杜红亮,夏 颂,徐 卓
(西安交通大学,电子陶瓷与器件教育部重点实验室,西安 710049)
0 引 言
水声换能器是潜艇、水面舰艇、鱼雷等水声装备实现水中导航与通讯、水中目标探测与识别和水声对抗的核心器件,压电材料是水声换能器的关键材料,直接影响和制约着水声换能器技术的发展。压电单晶复合材料作为新一代压电智能材料,具有压电常数高、机电耦合系数高等优势,可以显著提高换能器的带宽、灵敏度、分辨率等指标[1-9]。然而,目前关于压电单晶复合材料在水声领域应用的研究较少,尤其缺乏面向水声换能器的压电单晶复合材料设计方法。
不同类型水声换能器对压电单晶复合材料的性能要求不同,如发射型换能器为实现大功率宽带发射,要求材料具有高压电常数、高机电耦合系数;高灵敏度水听器要求材料具有高水声优值[10]。然而,同一材料难以同时实现所有指标最优化,所以,为充分发挥压电单晶复合材料的性能优势,关键是要根据水声换能器的具体应用需求对压电单晶复合材料的结构和性能进行设计。
本文根据均匀场理论、混合定律、串并联理论及有限元理论[11-12],提出了一种解析模型与数值模型相结合的设计方法。首先,采用解析模型建立压电相体积分数与复合材料宏观性能间的定量关系,随后针对具体的水声应用,选取最优体积分数进行数值求解,明确压电相和聚合物相的最佳结构参数,实现压电单晶复合材料的高性能化。最后,通过实验验证这种方法的有效性和准确性。
1 模型的建立
1.1 解析模型
压电相选取[001]极化的三方相Pb(In0.5Nb0.5)O3-0.47Pb(Mg1/3Nb2/3)O3-0.29PbTiO3(PIN-47%PMN-29%PT)压电单晶,呈4mm宏观对称性,聚合物相选取各向同性的环氧树脂(Epo-Tek 301),借助Smith厚度振动模式理论和静水压模式理论[13-14],推导出1-3型压电单晶复合材料的宏观等效性能参数表达式。
等效密度:
(1)
等效压电常数:
(2)
(3)
等效介电常数:
(4)
等效弹性刚度系数:
(5)
(6)
此外,根据IEEE压电测量标准中压电、介电及机电耦合性能之间的相互关系可以推导出1-3型压电单晶复合材料的等效厚度机电耦合系数、等效声阻抗和等效静水压性能等其它等效性能参数。
等效厚度机电耦合系数:
(7)
等效压电电压常数:
(8)
等效水声优值:
(9)
等效声阻抗:
(10)
等效静水压性能:
(11)
(12)
(13)
式中,v为压电相的体积分数,(1-v)为聚合物相的体积分数,密度ρ的上角标c代表压电单晶相,p代表聚合物相,弹性常数和介电常数带有上角标E和T表示压电单晶相,而无角标表示聚合物相,带横杠的量表示1-3型压电单晶复合材料的宏观等效性能参数。
[001]极化的三方相PIN-47%PMN-29%PT压电单晶和Epo-Tek 301环氧树脂的性能参数分别列于表1和表2。将两相材料的性能参数代入公式中求解所得即为1-3型压电单晶复合材料宏观等效性能参数的解析解。

表2 Epo-Tek 301环氧树脂在室温条件下固化24 h后的性能参数Table 2 The properties of Epo-Tek 301 epoxy cured at room temperature for 24 h
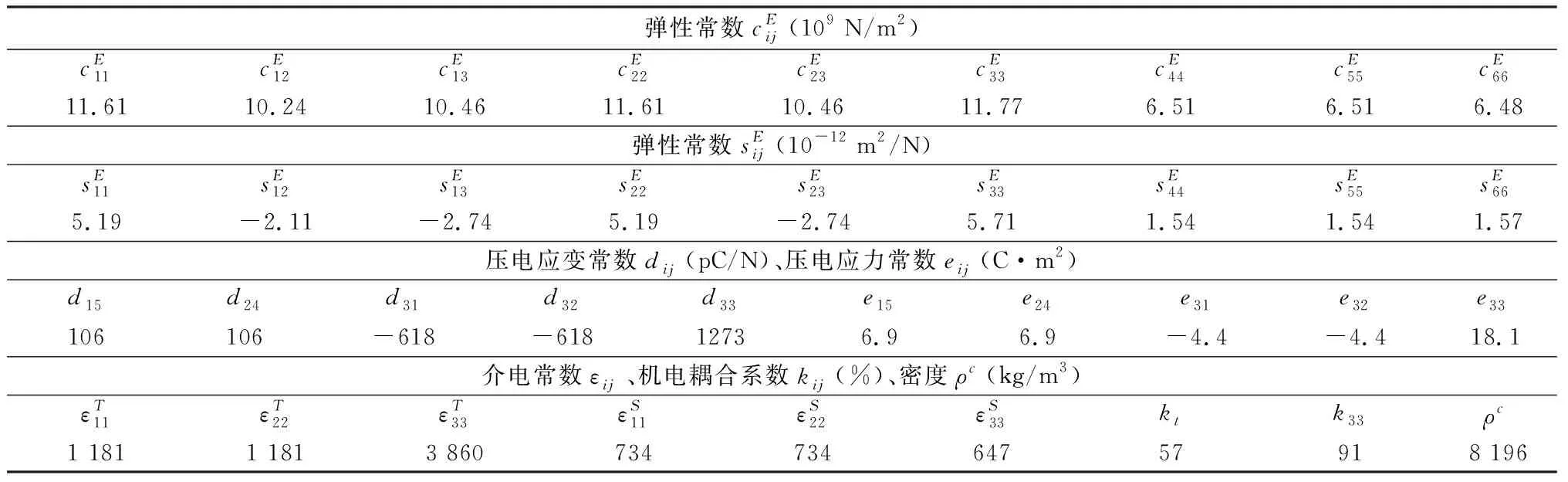
表1 [001]极化的三方相PIN-47%PMN-29%PT压电单晶的全套矩阵参数Table 1 The full matrix data of [001] poled rhombohedral PIN-47%PMN-29%PT single crystal
1.2 数值模型
1-3型压电单晶复合材料的结构示意图如图1(a)所示,压电单晶小柱平行排列于环氧树脂基体中,压电单晶复合材料与Z轴垂直的上、下表面被覆金属电极,柱宽为a,周期为d,压电相的体积分数可表示为v=a2/d2。利用有限元软件ANSYS,为便于计算,建立1/4周期有限元模型,如图1(b)所示,分析1-3型压电单晶复合材料的性能。
通过模态分析、谐响应分析分别得出1-3型压电单晶复合材料的振动模态、谐振频率和阻抗频谱,通过静态分析分别提取模型各个单元的单元体积、单元应力、单元电位移、单元电场,采用体积加权平均的方法[15]计算可得1-3型压电单晶复合材料的各项宏观等效性能参数。
2 设计方法
2.1 解析法
本文利用解析法求解了1-3型压电单晶复合材料的各项宏观等效性能参数随体积分数的变化规律,结果如图2(a)~(c)中实线所示。为了验证解析解的合理性与准确性,选取压电单晶小柱宽高比AR=0.1,压电相体积分数分别为10%、20%、30%、40%、50%、60%、70%、80%的压电单晶复合材料进行ANSYS有限元数值仿真计算,数值解结果如图2(a)~(c)中散点所示。将解析解与数值解进行对比分析,结果表明,采用解析模型和数值模型计算所得复合材料的各项宏观等效性能参数随体积分数的变化规律基本一致。可见,利用解析模型能够快速有效地确定复合材料中两相材料特性、体积分数的选取。以文中1-3型PIN-47%PMN-29%PT / Epo-Tek 301压电单晶复合材料为例,当压电单晶相体积分数v=50%~70%时,d33值和kt值较高,适用于发射型水声换能器的制作;当v=20%~40%时,d33·g33值、dh·gh值和kt值较高且Z值较低,适用于接收型水声换能器的制作;当v=40%~50%时,适用于收发共用型水声换能器的制作。解析法的优势主要在于根据器件的具体应用要求对复合材料性能的需求,灵活快速调整两相材料的特性,如压电单晶相组分、切型、极化方向的选取,聚合物相杨氏模量、泊松比的选取,提高材料设计效率,该方法可广泛应用于面向各种类型水声换能器的压电单晶复合材料的初步设计。
另外,对于一定体积分数的复合材料而言,其各项等效性能参数的解析解与数值解有所偏差,如压电常数d33和介电常数ε33的解析解均略大于数值解,该微小偏差主要由解析模型简化所致。解析模型假设压电复合材料的横向尺寸远远小于波长,即材料周期结构十分细密(即宽高比AR至少小于0.1),压电单晶相和聚合物相两相材料在厚度振动方向(即Z方向)应变相等,在水平方向应力相同,该假设未考虑压电相和聚合物相两相界面相互作用对复合材料性能的影响,偏离了复合材料的Z向位移和水平应力都呈现不均匀分布的实际情况[16]。上述微小偏差的累积叠加进而导致与d33和ε33密切相关的压电电压常数g33、水声优值d33·g33、静水压压电电荷常数dh等其它宏观等效性能参数的解析解与数值解之间出现较大偏差,但偏差的存在基本不会影响复合材料宏观等效性能参数随体积分数的变化规律。
2.2 数值法
上述解析结果已经明确建立了压电单晶复合材料宏观等效性能参数与体积分数的定量关系,根据水声换能器的具体应用要求,获取最佳体积分数,在此基础之上,采用数值法建立相应体积分数的压电单晶复合材料有限元模型,重点研究压电单晶小柱宽高比对复合材料综合性能的影响,获得最优结构参数,二者的有效结合能够快速准确地完成压电单晶相和聚合物相两相材料的材料特性、体积分数和结构参数的选取,以最大限度发挥压电单晶复合材料的优异性能。以面向发射型水声换能器的1-3型PIN-47%PMN-29%PT/Epo-Tek 301压电单晶复合材料为例,选取体积分数为50%,保持压电小柱高度t=3 mm不变,而改变压电小柱的宽度a=0.3 mm、0.6 mm、0.9 mm、1.2 mm、1.5 mm、1.8 mm、2.1 mm,通过研究压电单晶小柱宽高比对复合材料厚度振动模态与宏观等效性能参数的影响,确立压电单晶小柱的最佳宽高比。结果如图3(a)~(c)所示,随着宽高比的增大,1-3型压电单晶复合材料的谐振频率fr和反谐振频率fa均向低频方向移动,fr由366 kHz降低至317 kHz,降低了49 kHz,fa由599 kHz降低至569 kHz,降低了30 kHz;介电常数ε33增大5.5%,压电常数d33减小8.5%,声阻抗Z减小5%,kt值增大4.3%,这是由宽高比与两相材料界面处的应力传递效应密切相关所致[17]。此外,宽高比对厚度振动模态的纯化也有影响,当宽高比AR≥0.4时,在10 kHz~1 MHz频率范围内除厚度振动模态之外,阻抗-频率和相角-频率特性曲线的高频处出现横向结构振动模态,其振动特性与复合材料的周期结构密切相关[18],该模态的一阶和二阶谐振频率随着宽高比的增大均向低频方向移动,当宽高比AR=0.7时,厚度振动模式反谐振峰处出现劈裂,横向结构振动模式与厚度振动模式发生相互耦合,可见,当1-3型压电单晶复合材料用于发射型换能器时,为获得纯净的厚度振动模式,宽高比的取值范围为AR≤0.6,为同时满足大声源级、宽带发射对高压电常数、高机电耦合系数、低声阻抗的需求,最佳宽高比AR=0.3。
作为解析法的有效补充,利用数值模型对复合材料进行设计的方法可推广至不同形状(如平面状、曲面状、球冠状、弧线状)、不同种排列方式(如非均匀、不规则排列)、各种压电小柱形状参数(如方形、三角形、六边形)的压电单晶复合材料的设计,准确高效地确立压电单晶复合材料的最优结构参数。
2.3 实验验证
为了对解析模型与数值模型相结合的综合设计方法的准确性与可靠性进行评估,采用切割-填充法制备出尺寸约为17 mm×17 mm×3 mm、压电相体积分数为50%、宽高比为0.3的1-3型PIN-47%PMN-29%PT/Epo-Tek 301压电单晶复合材料。实验测试和数值计算所得压电单晶复合材料厚度振动模式的阻抗-频率特性曲线如图4所示,二者高度吻合。表3分别列出压电单晶复合材料的宏观等效性能参数的实验值、数值解、解析解,对比发现,通过三种方式所得压电单晶复合材料的各项宏观等效性能参数基本一致,三者之间只有微小差别。其中,数值解和解析解之间的微小偏差及形成原因在前文已有叙述,实验值与数值解之间也存在微小偏差,这主要是由实验制备工艺和测试误差引起。该实验结果有力证实了解析模型与数值模型相结合的压电单晶复合材料综合设计方法的准确性和可靠性。

表3 1-3型压电单晶复合材料的宏观等效性能参数的数值解、解析解、实验值以及压电单晶材料性能的比较Table 3 The comparison between the numerical solutions, analytical solutions, experimental values of the 1-3 piezoelectric single crystal composite and the properties of the single crystal
此外,压电单晶复合材料的性能与拟采用的压电单晶材料的自身性能密切相关,表3列出了通过实验制备的压电单晶复合材料和所使用的压电单晶材料的性能。由表可知,与单相压电单晶材料相比,压电单晶复合材料在保持压电常数d33和介电损耗tanδ没有明显恶化的情况下,其介电常数ε33、谐振频率fr和反谐振频率fa、厚度机电耦合系数kt以及声阻抗Z均得到显著改善,更有利于水声换能器的带宽和电声效率的提高以及电阻抗和声阻抗匹配。值得一提的是,2019年Li等[19]研制出了钐掺杂Pb(Mg1/3Nb2/3)O3-PbTiO3(PMN-PT)压电单晶,其压电常数d33高达4 000 pC/N,是PMN-PT单晶压电常数的2倍[20]。采用上述压电单晶材料,通过合理的设计与优化,可实现压电常数d33≥3 500 pC/N的超高性能压电单晶复合材料的制备。
3 结 论
针对不同类型水声换能器对压电单晶复合材料性能的不同需求,提出了一种设计方法,即:解析模型与数值模型相结合。首先,采用解析模型快速建立压电单晶复合材料宏观等效性能参数与压电单晶相体积分数之间的定量关系,在此基础上,利用数值模型重点研究宽高比对压电单晶复合材料振动模式和宏观等效性能参数的影响。最后,通过实验证实了两种模型相结合对压电单晶复合材料设计的有效性和准确性。该综合设计方法的主要优势在于根据不同类型水声换能器对压电单晶复合材料的具体要求,利用解析法灵活调整两相材料的特性,如压电单晶相的组分、切型、极化方向和聚合物相的杨氏模量、泊松比等,利用数值法广泛研究复合材料形状(如平面状、曲面状、球冠状、弧线状)、单晶小柱排列方式(如非均匀、不规则排列)和结构参数(宽高比)对压电单晶复合材料综合性能的影响,二者结合能够准确高效确立两相材料的材料特性、体积分数和结构参数的选取,以最大限度发挥压电单晶复合材料的性能优势,满足不同类型水声换能器的应用需求。与传统的由材料性能决定器件性能的方式不同,该套方法的提出可以完成由器件性能指导的复合材料的实验设计,实现材料由被动选择到主动赋能,对面向水声换能器的压电单晶复合材料的设计开发及生产、应用具有重要意义。

