“零弯矩”理论及其在连续刚构桥监控中的应用

何 智 李娟娟

1.四川省兴冶岩土工程检测有限责任公司；2.四川省冶勘设计集团有限公司

1 引言

随着国家“一带一路倡议”政策推进以及西部大开发的战略布局，我国正向交通强国迈进，交通基础设施的建设在西部仍占重要的地位。作为跨越山谷、河流的大跨度桥梁，对其进行施工监控是保证桥梁顺利竣工的重要手段。连续刚构桥属于超静定桥跨结构，结构线形和主梁恒载内力与施工过程相关联，为了使结构实际状况与设计状态产生的偏差较小，保证结构的线形符合设计，内力状态处于最优，必须进行有效的施工监控。

连续刚构桥在长期运营过程中，普遍出现跨中下挠、开裂等病害，因此，保证桥梁整个生命周期内具有良好的线形就尤为关键，当前，广泛采用的是施工过程中设置合理的预拱度来实现线形控制。钟建国等[1]分析了连续刚构桥施工监控中影响线形控制的因素，并将其用于桥梁监控中。余明等[2]探讨了灰色系统理论在连续刚构桥线形控制中的应用，得出了最优立模标高，指导了工程施工。曹淑上等[3]提出了设置预拱度的长期增大系数以及按余弦曲线分配预拱度的方法。任山江[4]在其学位论文中对挂篮变形值开展了研究，提出了采用数学公式预测挂篮变形。由此可见，不同的研究者对于连续刚构桥线形控制有不同的见解，多数研究者均从影响预拱度因素的角度出发考虑线形问题。

对于预拱度中成桥预拱度如何取值，保证结构在经过一段时间的运营后与理论线形最大程度吻合是本文进行探讨的初衷。

2 恒载零弯矩理论

大量的统计资料表明，连续刚构桥跨中下挠已成为该类桥梁最主要的病害，在下挠不明显的情况下，梁体尚可满足正常使用，当下挠到一定程度后，跨中梁体有相对变短趋势，底板预应力会减小，梁体开始出现裂缝，裂缝的出现，削弱了截面刚度，从而导致梁体挠度增加，进入恶性循环。

如表1所示，当挠跨比处于较小水平时，梁体未出现开裂现象，结构处于运营良好状态；当挠跨比较大时，梁体普遍出现开裂现象，结构需进行加固处治方可继续运营使用。

表1 部分连续刚构桥跨中下挠及开裂情况

如果采取合理可行的方法使连续刚构桥跨中挠度得到控制，在后续的运营过程中，预应力损失亦会有所减小，能较大程度地保证梁体完整不开裂。考虑降低跨中挠度，率先被考虑的是增大截面刚度，从增加材料弹性模量以及加大截面尺寸等方面入手，材料弹性模量增加是有限的，一味追求高强度的混凝土必然造成不经济且技术上亦无法实现，加大截面尺寸又导致梁体自重增加，不能明显降低其恒载挠度，因而，普遍寻求其他解决方法。通常在设计阶段，考虑桥梁的承载荷载主要有结构自重、运营阶段的移动荷载、混凝土的收缩徐变效应等，结构自重在桥梁建成后变形已经完成，移动荷载亦不会有较大变化，业内广泛认为混凝土的收缩徐变是造成跨中下挠的主要因素。

混凝土的收缩徐变尚无十分准确的计算方法，考虑由其引起的下挠通常有三种思路：一是从本质上研究，从混凝土原材料的角度出发，改善原材料和添加外加剂等使混凝土在后期产生的徐变较小，进而对桥梁的挠度影响较小；二是选用合理的结构设计，使梁截面处于较小的应力水平，以减小混凝土的徐变；三是配置合理的预应力，使其产生的内力与混凝土自重产生的内力相互抵消，恒载作用下截面内的弯矩为零，以使结构产生较小的挠度甚至不产生挠度，即恒载零弯矩理论。初始挠度较小，后续徐变对其影响亦会减小。范立础院士在《预应力混凝土连续梁桥》[5]一书中提出这一基本原理，文献[6]则基于恒载零弯矩理论对结构进行预应力优化设计，有效降低了梁体在恒载作用下的变形。

采用零弯矩设计理论的工程实例有以下几点。

（1）佛山石南大桥，该桥为我国第一座采用零弯矩理论设计的连续刚构桥，在设计过程中，配置的预应力使断面弯矩处于很小的水平，主梁的恒载弯矩基本接近零，因而由徐变产生的挠度亦大大减小，运营13年后跨中仅下挠3cm。

（2）湖南省湘潭湘江大桥、安乡大鲸港大桥等均采用了恒载零弯矩理论进行设计施工，后期运营状况良好。

（3）从上世纪末起，国内的一些省市陆续推广零弯矩设计理念，江西建成了乐安河大桥、赣江西支特大桥，湖南建成了益阳资江二桥、常德石龟山大桥等。

恒载零弯矩理论就是以挠度为目标，配置合理的预应力（对于跨度较大的桥梁，可配置体外预应力进行实现），既保证梁体强度满足规范要求，又要使预应力产生的弯矩尽可能抵消悬臂施工自重弯矩，梁体施工过程中不发生挠度，亦无初始转角，从理论上来说，在徐变作用下，就不会产生竖向挠度。显然，当混凝土徐变产生的挠度较小，势必会有利于桥梁运营一段时间后的挠度控制，因此，主要考虑成桥后下挠影响的成桥预拱度亦可取用较小的值。

3 基于零弯矩理论的预拱度设置

3.1 内力包络设计对成桥挠度的影响

现行《公路钢筋混凝土及预应力混凝土桥涵设计规范》[8]等规范均是以分项系数表达的极限状态方法进行设计，关于弯矩、剪力等承载能力极限状态的本质是材料的强度问题。这一方法是要求结构外荷载作用下的内力应不超过截面承载能力，根据成桥时最不利状态下的内力（不含预应力）布置预应力，在考虑预应力损失和次内力后，使结构各截面的内力位于承载力包络图之内，并有一定的安全储备，再根据变形、开裂验算情况进行调整即可。

对于连续刚构桥，因其跨度较大，要充分利用其圬工性能，预应力钢束就尤为重要，其主要意义就在于其确保施工全过程及成桥后结构的强度指标满足设计要求。从包络设计这一角度出发，能满足截面承载力大于外荷载作用下内力的预应力配置方式有很多种，这是一个相对宽泛的设计原则，桥梁设计者往往都是满足于规范的验算要求，未深入分析结构整体的内力分布情况。从前文分析可知，并非配置的预应力越多越好，过多的预应力束会增加施工难度，削弱截面刚度，亦可能导致施工过程中不平衡弯矩增大。本文对部分连续刚构桥进行了考虑施工过程的计算分析，施工过程中，梁体应力均未超出材料限值，成桥后的跨中挠度差异明显，见表2所示。

表2 连续刚构桥成桥挠度计算

综上所述，尽管桥梁设计者均采用了内力包络设计的原理保证截面应力未超出材料限值，但成桥时相对挠度差异明显。这说明基于强度的结构设计，配置不同的预应力会导致成桥挠度有明显的差异。结合恒载零弯矩理论可知，若设计时既考虑桥梁结构的强度满足规范要求，同时尽量使主梁在恒载作用下的弯矩处于较小范围，亦即施工过程中梁体初始挠度和初始转角较小，当混凝土徐变发生时，其产生的挠度就较小。

3.2 预拱度

对于大跨度预应力混凝土连续刚构桥，合理地设置预拱度可抵消支架、梁体自重、活载及混凝土收缩徐变产生的变形，从而保证梁体在充分变形后与设计状态一致。业内普遍习惯将预拱度分为施工预拱度和成桥预拱度。施工预拱度的设置主要是为了消除连续刚构在悬臂施工过程中诸如当前节段湿重、挂篮重量等各种施工荷载对线形的影响，可通过计算分析确定各阶段的施工预拱度值。成桥预拱度的设置主要是考虑后期运营过程中的荷载以及混凝土收缩徐变的影响。运营过程中诸如汽车、人群等荷载产生的挠度可以建立有限元模型计算得到，而混凝土收缩徐变则主要依托经验性计算。混凝土的收缩徐变目前普遍采用Dischinger 老化理论、混合理论和弹性理论，加之结构的几何非线性和徐变挠度的耦合效应，更难以准确分析其影响，设计时，一般按常规收缩徐变曲线的变化规律并赋予一定的安全储备来考虑这一因素。当前，成桥预拱度一般都是根据计算结果并附加经验值按某种曲线分配给各个节段[7]。显然，若结构设计时配置的预应力筋既能满足强度设计要求，又考虑了“恒载零弯矩”理论，成桥后期由于收缩徐变效应导致的下挠就偏小，因而，采用较小的成桥预拱度值即可使桥梁运营期间的线形与设计状态吻合一致。

4 工程应用

某三跨混凝土连续刚构桥，其跨径组合为（65+125+65）m，边中跨比为0.52，箱梁根部梁高7.5m，跨中及端部梁高2.7m，梁高按1.8次抛物线变化，横断面为单箱双室直腹板箱梁。设计为三向预应力体系，钢束锚下张拉控制应力为1358MPa。主墩采用矩形双肢薄壁墩，墩高为16m 和16.7m，矩形截面尺寸为13×1.6m，下设承台个嵌岩桩基础。桥面全宽19.25m，两侧设置护栏，右侧设有宽4.0m 的人行道，设置单向1.5%横坡。桥梁立面和主梁断面见图1～图2所示。

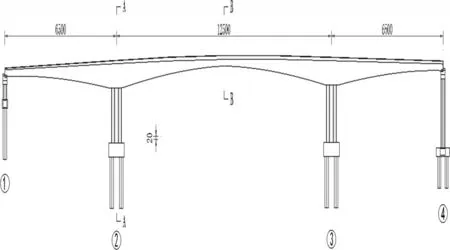
图1 桥梁立面示意图（单位：cm）

图2 主梁断面示意图（单位：cm）

采用有限元软件对其施工过程进行正装计算分析，最大悬臂状态主梁的挠度见图3所示。本桥在恒载作用下跨中的最大挠度仅为30mm，其挠跨比为L/4167。与表2进行对比，其挠跨比明显小于其他几座类似桥梁。

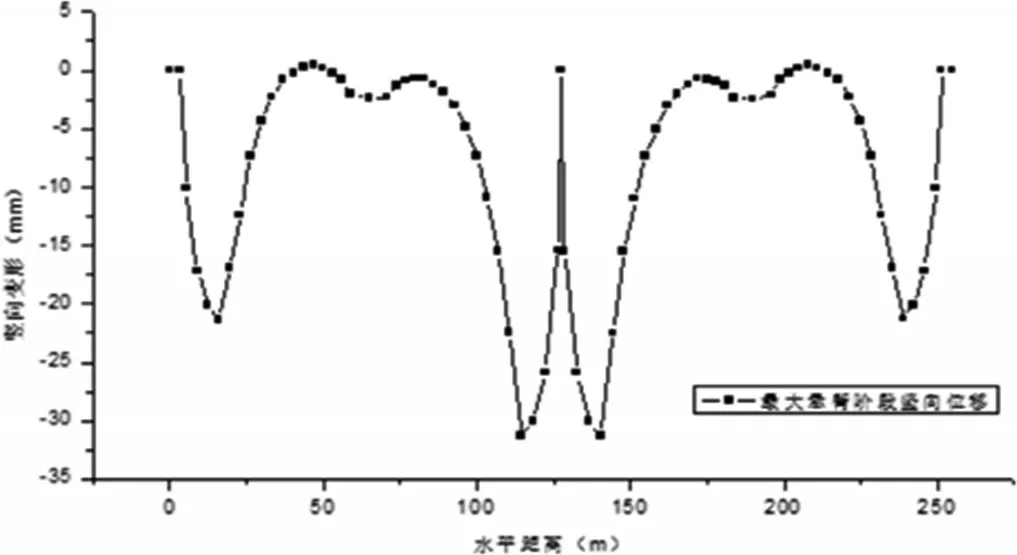
图3 最大悬臂阶段主梁竖向挠度曲线

为进一步分析施工过程中预应力与恒载产生的作用效应，对该桥在施工阶段预应力产生的弯矩、自重等其他施工恒载作用下产生的弯矩进行计算分析，结果见图4～图5 所示。由计算结果可知，在施工过程中，预应力产生的弯矩能较好的抵消自重等荷载作用的弯矩，亦说明本桥在恒载作用下产生挠度较小是合理的。

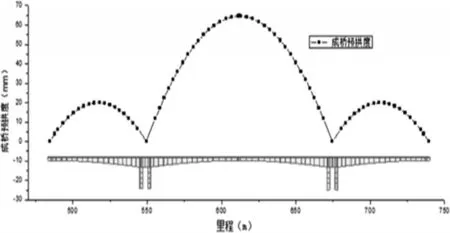
图4 竣工后在自重等恒载作用下箱梁弯矩

图5 竣工后预应力钢束一次作用下箱梁弯矩

综上所述，根据零弯矩的设计理念，本桥可适当采用较小的成桥预拱度。对于中跨，参考一般经验取值范围（L/2000～L/1000），本次监控取其下限，近似取值65mm；边跨根据经验取值为中跨的1/4～1/3，确定本桥边跨成桥预拱度取值为20mm。本桥主梁的底板厚度和梁高按1.8次抛物线变化，二次抛物线分配能与主梁线形吻合，成桥后线形更美观。因此，本桥中跨和边跨均采用二次抛物线成桥对预拱度进行分配计算，得到成桥预拱度如图6所示。

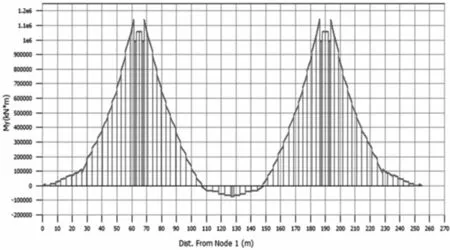
图6 成桥预拱度

5 结束语

现行规范采用内力包络对桥梁进行强度设计，设计者对预应力的配置有很大的主观性。通过对零弯矩理论的阐述，分析不同跨度的连续刚构其挠跨比差异较大，得到以下结论：

（1）基于内力包络原理进行结构设计，能保证应力不超出材料限值，同时尽可能实现恒载零弯矩，这对控制连续刚构挠度是有益的。

（2）若预应力产生弯矩能较好抵消结构自重产生弯矩，其恒载作用下的挠度也必然较小，在施工监控时可适当设置较小的成桥预拱度。