改进的自适应参数DBSCAN 聚类算法

王 光，林国宇

辽宁工程技术大学 软件学院，辽宁 葫芦岛 125105

1 引言

聚类算法是在无标签的数据中发现数据的内部联系，若数据的属性相同则聚成一个簇。针对这一特性，聚类算法被广泛应用于用户画像[1]、文本处理[2]、图像分割[3]等领域。

DBSCAN算法是密度聚类中最经典的算法之一，它可以有效地寻找到被低密度区域分隔的高密度区域，并在具有噪声的数据中发现任意形状的簇。DBSCAN通过邻域(Eps)和邻域内最少样本的数量(MinPts)来识别数据集中有较高密度的样本点，并将其划分为簇。然而DBSCAN对Eps和MinPts两个参数的选择非常敏感，若选取不当可能会出现错误的聚类甚至无法聚类的情况。针对DBSCAN参数的自适应选择，国内外学者进行了一系列的研究。周红芳等[4]提出的I-DBSCAN算法运用极大似然估计和泊松分布来估计Eps的取值，用求数学期望的方法来求MinPts，该方法依赖数据自身的分布特点，依靠人为观察噪声和聚类个数与K的关系图，导致结果存在一定误差。李文杰等[5]提出的KANN-DBSCAN算法根据K-近邻求出Eps的候选集合，选取不同的K值根据数学期望得到MinPts，再把参数输入DBSCAN继续聚类，当取三次K值，若簇数稳定则记为最优簇数，通过循环迭代求出最优参数，该方法虽然精确度相对较高，但是随着数据量的增大，时间消耗也逐渐增大。周治平等[6]提出的AF-DBSCAN根据k-dist分布进行分析，该方法用一条曲线描述全局分布，主观性较强同时存在一定的误差。秦佳睿等[7]提出的SALE-DBSCAN通过寻找密度峰值点，自动选择聚类的局部邻域半径，该方法需要计算所有点的局部密度来寻找密度峰值点，再扩张密度峰值点邻域、合并聚类结果等，使该算法的复杂度较高。李宗林等[8]提出利用非参数核密度估计来确定Eps和MinPts，该算法虽然实现了参数的全程自适应选择，但是针对不同类型的数据进行聚类时鲁棒性较差，且计算复杂度较高。

鉴于此，本文提出一种自适应选择DBSCAN参数的KLS-DBSCAN聚类算法，该算法利用数据自身的分布特点找出合理的参数范围，再通过寻找聚类内部度量最大值的方法确定最佳的Eps和MinPts参数值，该算法有运算简单、聚类结果准确率高的优点。

2 DBSCAN算法

DBSCAN算法由Ester M、Kriegel H P等人[9]在1996年提出，它不需要预先指定簇的个数，但需要给定两个参数。该算法是基于一组：“邻域”参数(Eps,MinPts)来描述样本分布的紧密度，假设给定数据集D={x1,x2,…,xm}定义如下概念：

定义1(Eps-邻域）对 xj∈D,Eps-邻域包含样本集D中与xj之间的距离小于等于Eps的样本，即：

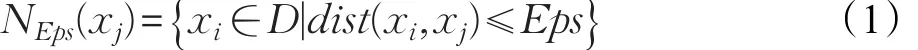
定义3（直接密度可达）如果xj在 xi的Eps-邻域中，并且xi是核心对象，称xj由xi直接密度可达。

定义4（密度可达）对于xi和xj，如果存在一个序列 p1,p2,…,pn，其中 p1=xi,pn=xj并且 pn+1由 pi直接密度可达，称xj由xi密度可达。

定义5（密度相连）对于 xi和 xj，如果存在 xk使

定义2（核心对象）如果 xj的Eps-领域至少包含MinPts个样本，即：xi和xj均由xk密度可达，则称xi和xj密度相连，密度相连具有对称性。

定义6（簇和噪声）从数据集D中任取一点 p，从p点开始在D中搜索满足Eps和MinPts条件且密度可达的所有点构成一个簇，不属于任何簇的对象则被标记为噪声点。

在具体的DBSCAN聚类过程中首先将数据集D中的样本标记为未处理对象，对每个样本点计算Eps半径内点的集合，集合内多于MinPts个数的点标记为核心点，剩余的点如果在核心点的邻域内则被标记为边界点，否则标记为噪声点。

3 自适应确定DBSCAN算法参数

3.1 基本思想

密度聚类算法的实质是根据空间中数据分布的紧密程度进行聚类。DBSCAN算法通过Eps和MinPts两个参数来刻画数据的紧密程度，在传统的DBSCAN算法中，Eps和MinPts两个参数的选择往往通过经验判断，再根据结果调整，因为Eps和MinPts两个参数具有全局性，在分布不均的数据上采用经验数据很难达到预期效果。

本文通过DBSCAN算法在不同数据集上的实验发现，达到预期聚类效果时Eps和MinPts两个参数值并不唯一，但一定在某个区间内变化。无论数据疏密程度、形状，数据的局部密度往往存在一定的变化，因此可以预知数据分成几个簇比较合理，基于以上研究采用核密度估计确定参数合理区间，根据局部密度分析确定聚类簇数，通过计算轮廓系数求出最优的Eps和MinPts两个参数值。

3.2 确定参数Eps和MinPts的合理区间

根据数据分布特征来判断参数范围，能有效地将参数确定在一个相对合理的区间。核密度估计能够刻画数据分布特征[10]，并且能有效地检测出噪声点[11]，是一种非参数方法，假设独立分布F包含x1,x2,…,xn个样本点，概率密度函数为 f，核密度估计如下：

其中，h表示带宽，K(x)表示核函数，同时K(x)满足以下条件：

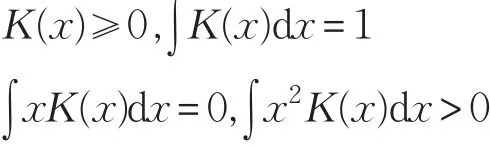
然而带宽的选择往往比较困难，不同的带宽会导致拟合的结果有很大的差异，通常在聚类分析中，一般选择均平方积分误差函数(MISE)来优化带宽。具体定义如下：

在弱假设下：

其中：

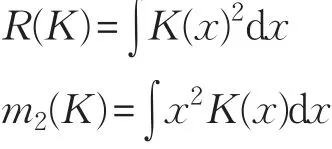
最小化MISE(h)等价于最小化AMISE(h)，求偏导并令导数等于0有：

其中m、R根据核函数确定。

然而，核密度估计并不能找到实例中的最优参数，但是可以估计一个合理的参数选取区间。下面通过一个实例进行具体分析。

生成包含2 000个数据点4个聚类中心的数据集SampleD，分布情况如图1所示，计算所有样本之间的距离，生成距离矩阵Dist，通过核密度估计的方法绘制曲线图，如图2所示，可以发现密度曲线出现了两次峰值，第一次峰值的出现代表簇内密度较高的距离，第二次峰值的出现代表簇间密度较高的距离。所以本例中应该取簇内距离作为Eps的取值，当Eps∈( )0,0.2时可以作为Eps取值的候选范围。

图1 SampleD的数据点分布图

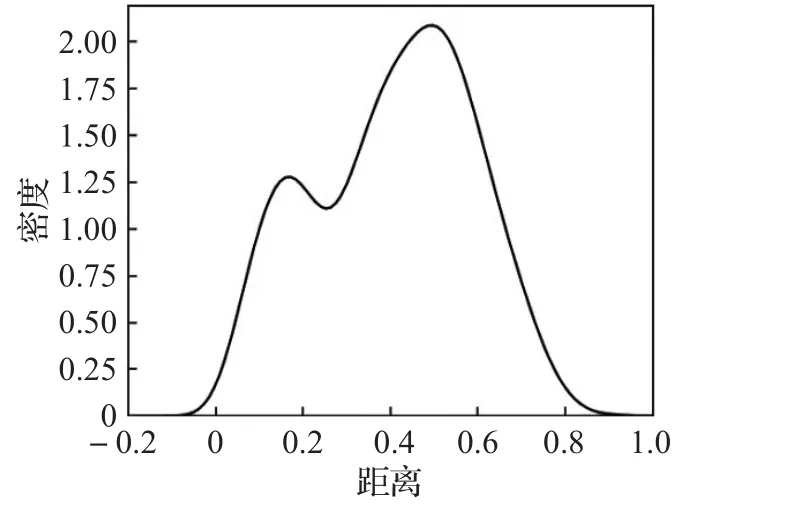
图2 核密度估计曲线图

根据Eps的预估值范围，采用数学期望的方法，根据距离矩阵Dist，在给定数据集中求出MinPts的合理区间，公式如下：

其中，Pi表示对象i的Eps邻域内包含的样本个数。

3.3 确定聚类簇数

通过核密度估计对全局数据进行分析只能粗略地得到数据集的疏密程度，然而对局部密度特点分析可以计算出数据集合理的聚类簇数[12]，密度峰值聚类算法（DP）正是利用这样的特性确定聚类中心，然而DP算法仍然需要人工指定截断距离(dc)，并且最终的聚类中心的选择通过观察得到。本文利用带宽参数自适应选择截断距离，通过计算决策图中样本点之间的斜率，分析比较疑似中心点之间的距离关系确定聚类中心，具体描述如下：

在给定的数据集D中随机取一点g，可以定义两个值：局部密度ρi和到较高局部密度点的距离δi。

局部密度 ρi：

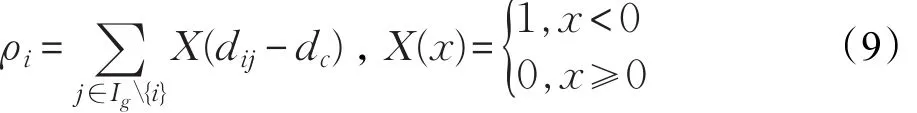
其中，dij表示两点间距离，dc表示截断距离，dc可根据上文中提到的带宽参数自适应确定[10]。

集合D中每一个样本点 xi通过(ρi,δi),i∈ID抽象表示，并绘制如图3所示决策图。

图3 聚类中心决策图

为了更精确选择聚类簇数，综合考虑ρi和δi的影响，定义 γi=ρiδi,i∈Is,γi值越大，越有可能是聚类中心[13]。对 {γ}Ni=1进行降序排列，p 表示 γ[1～p]与 γ[p～n]之间变化程度最大的点，点p满足：

其中，ki表示第i个点到i+1个点之间线段的斜率，φ表示相邻点斜率差的平均值，θ(j)表示相邻点斜率差的总和。疑似聚类中心定义为：

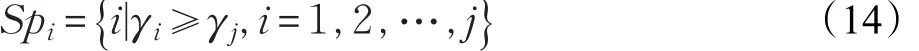
根据密度峰值算法的性质，真实的聚类中心一般分布在密度较高的区域，且中心之间相对距离较远。如果在一个高密度区域中存在多个疑似聚类中心点，通常这些点会比较接近。因此依次判断最大值的γi和剩余点之间的最短距离，如果小于截断距离dc，则不是聚类中心，如果大于截断距离dc，则是聚类中心。

3.4 参数寻优

在真实分类标签未知的情况下可以通过内部度量来描述聚类的质量，计算轮廓系数是常用的聚类内部度量方法[14]，它是衡量一个样本点与它所在簇相比于其他簇的相似度，具体公式定义如下：其中，a(i)表示第i个对象到所在簇中其他对象的平均距离，b(i)表示第i个对象到除了i所在簇以外的其他簇内对象的平均距离。s(i)∈[-1,1]该数值越接近于1说明分类越合理。

本文引入轮廓系数作为衡量聚类效果的重要指标，因为它不需要在明确聚类中心的情况下就能计算出簇与簇之间的密集与分散程度，并且具有鲁棒性。利用轮廓系数的这一特点计算出DBSCAN中最优的Eps和MinPts参数值，对数据集SampleD进行聚类的结果如图4所示，通过自适应选择参数能够识别密度较高的区域，并作出正确的聚类，说明本文算法选择了合适的Eps和MinPts两个参数。

图4 基于KLS-DBSCAN的SampleD聚类结果

3.5KLS-DBSCAN算法描述

（1）根据原始数据分布特征，利用核密度估计确定Eps范围，采用数学期望法确定MinPts范围。

（2）通过分析局部密度特点计算出数据集合理的聚类个数。

（3）采用轮廓系数作为衡量聚类质量的依据，从而确定最优的Eps和MinPts两个参数。

（4）利用最优的Eps和MinPts进行聚类。

具体计算过程如下所示。

算法 KLS-DBSCAN算法

输入：Eps的区间(eps_list)、Minpts的区间(Minpts_list)、最优的聚类个数(label_num)。

计算：

步骤1对eps_list、Minpts_list按最小间隔进行分割。

步骤2按照eps_list和Minpts_list的取值计算聚类个数。

步骤3如果所计算的聚类个数等于label_num，则计算轮廓系数。

步骤4比较轮廓系数，选取最大值。

步骤5储存轮廓系数的最大值所对应的Eps和MinPts值。

输出：全局最优的Eps和MinPts。

4 实验及结果分析

KLS-DBSCAN算法采用Python语言实现，在Windows10系统下运行，PC硬件配置：Inter®CoreTMi5-3337U CPU@1.80 GHz，8 GB内存，1 TB硬盘。为了证明本文算法具有较高的聚类准确率，实验通过对不同形状且密度分布不均的人工数据集和真实的UCI数据集进行分析。同时与KNN-DBSCAN、AF-DBSCAN及DBSCAN算法进行对比，其中KNN-DBSCAN基于K-平均最近邻法和数学期望生产密度阈值列表，通过参数寻优策略寻找聚类结果稳定区间，自适应选择最佳参数。AF-DBSCAN基于数学统计方法与密度聚类相结合，通过改进区域查询方法，搜索最优拟合模型，从而得到最佳参数。

4.1 人工数据集的准备及实验

为了验证KLS-DBSCAN算法的可行性，采用四种典型人工数据集进行实验分析，并用F值[15]对结果进行分析，F值综合了准确率和召回率，取值范围在(0,1]，越接近于1表示聚类效果越好。数据集可视化后如图5所示，R15是包含600个对象的二维数据集，Flame是包含240个对象的二维数据集，Aggregation[16]是包含788个对象的二维数据集，Spiral[17]是包含312个对象的二维数据集。

DBSCAN算法Eps参数的选择通过绘制k-距离曲线观察后得到，MinPts则根据经验采用数据集内样本数量的1/25[18]。通过聚类结果对比，如图6所示，发现KLS-DBSCAN和KNN-DBSCAN算法的聚类准确率更高，并且在不同数据集上都有良好的表现。具体的评价指标如表1所示。

从二维数据集上的聚类结果分析来看，在R15、Flame、Aggregation、Spiral数据集上，KLS-DBSCAN 和KNN-DBSCAN算法能够有效地识别桥接簇和非球形簇，同时F值接近于1。AF-DBSCAN和DBSCAN由于Eps的选择通过绘制k-距离曲线观察后得到，所以带有一定的主观性，传统DBSCAN算法的MinPts采用了经验数据，不能很好地适应不同的数据集，聚类过程不能有效识别其聚类簇。从总体分析，KLS-DBSCAN算法的聚类结果要明显优于AF-DBSCAN和DBSCAN算法，证明了其在不同形状、不同密度的数据集上有相对较高的准确率。

4.2 真实数据集的实验结果及分析

图5 人工数据集散点图

图6 KLS-DBSCAN与其他算法聚类结果对比

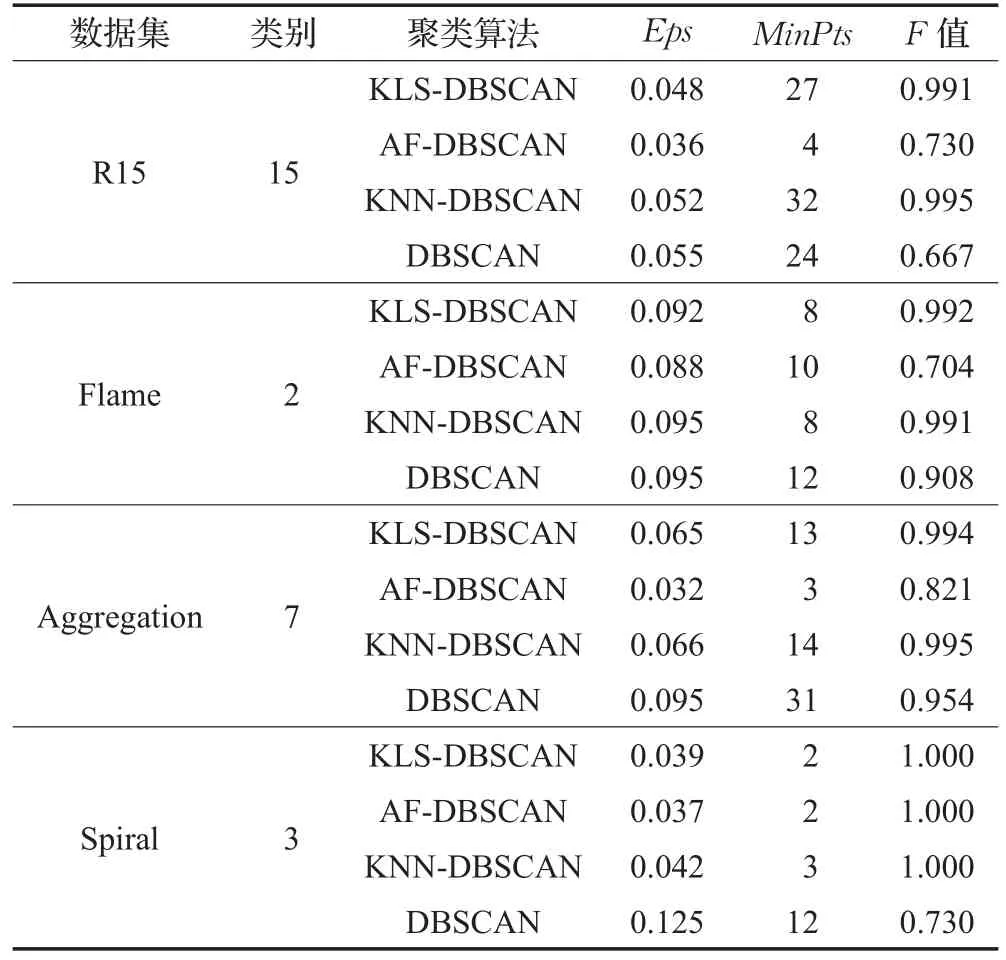
表1 人工数据集聚类指标对比

为了验证KLS-DBSCAN算法在真实数据集上的性能，通过真实的UCI数据集进行实验，并采用准确率（ACC）[19]、互信息评分（AMI）、调整兰德系数（ARI）[20]三个指标做综合评价，其中ACC的取值范围在[0,1]，AMI和ARI的取值范围在[-1,1]，值越接近于1说明与真实聚类结果越吻合。Iris是包含150个对象的4维数据集，Wine是包含178个对象的13维数据集，Sym是包含350个对象的2维数据集，Heart是包含303个对象的13维数据集。

真实数据集聚类指标如表2所示，可以看出本文算法KLS-DBSCAN克服了传统算法的人工选取参数的主观性，并在高维度数据集上也有良好的表现，在Sym、Wine、Heart数据集上的指标整体上优于KNN-DBSCAN、AF-DBSCAN和DBSCAN。

表2 真实数据集聚类指标对比

在Iris数据集上AF-DBSCAN算法表现更好，但该算法在不同分布不同维度的数据集上的性能不稳定，鲁棒性较差。KNN-DBSCAN算法虽然在二维的人工数据集上有良好的表现，但是在高维真实数据集上表现一般，因为其通过观察聚类结果簇数与K的关系图来选择Eps和MinPts，但是在分布不均的高维真实数据集上关系曲线很难进入稳定区间，K值的选择对聚类结果影响很大，本文算法则不会出现类似情况，即使通过核密度估计图选择了过大的Eps范围，也可以通过增加迭代次数确定最优的参数。

4.3 算法复杂度分析

对于二维数据集，传统的DBSCAN算法的时间复杂度为O(n2)[21]，本文算法基于DBSCAN，其时间复杂度主要来自于：（1）在选取最优参数时需要对Eps和MinPts参数范围同时循环计算；（2）局部密度ρi和到较高局部密度点的距离δi；（3）选择全局最优的Eps和MinPts参数。各部分的时间复杂度均为O(n2)，因此总的时间复杂度为O(n2)。

DBSCAN算法的空间复杂度为O(n2)，KLS-DBSCAN算法的空间复杂度主要来自于存储距离矩阵Dist，其空间复杂度为O(n2)。所以KLS-DBSCAN算法总的空间复杂度为O(n2)+O(n2)。

综上所述，KLS-DBSCAN算法的复杂度比传统的DBSCAN算法略有提升，但是保证了在一般场景情况下聚类的准确率。

5 结束语

传统的DBSCAN算法对参数的选择十分敏感，本文提出改进的自适应参数KLS-DBSCAN密度聚类算法，通过数学统计方法，建立数学模型，自动选择全局最优的Eps和MinPts两个参数。实验表明，本文算法实现了参数的自适应选择，同时准确率平均提高6.1%。但也存在不足之处：提高了聚类准确率的同时也牺牲了时间复杂度；对于密度差异大，维度比较高的数据集聚类效果一般。有效解决这些问题是下一步研究的方向。