改进量子搜索算法及其在核属性求解上的应用
谢旭明,段隆振,邱桃荣,杨幼凤
南昌大学 信息工程学院,南昌 330031
1 引言
量子计算能够并行地搜索待求解空间。由于这个特性,大量学者对量子计算进行研究。然而,量子计算并不能确定地得到待求解问题的解,而是以一定的概率得到解。因此,如何提高得到目标分量的概率成为量子计算的一个重要研究方向。Grover算法[1]是经典的量子算法之一,实现了无序数据库搜索问题的平方根级加速。自提出以来,Grover算法的普遍适用性使其得到了广泛的关注。
在Grover算法的应用方面,不少学者都进行了研究。彭宏等[2]的无线量子网络路由算法可以在限定的步骤内计算出目标路径;阮越等[3]将Grover算法融入主成分分析中,对原算法而言有着平方根的加速;孙国栋等[4]将Grover算法应用到求根问题上,将求根问题的时间复杂度降低到
在Grover算法的效率提升方面,也有许多学者进行了深入的探索。Grover算法比较突出的问题是:当目标分量占比超过1/4时,算法得到目标分量的概率急剧下降;且当目标分量占比过半时,算法会失效。针对这些问题,学者们提出了许多改进的方法。张煜东等[5]提出将原算法的搜索范围扩大一倍,从而使得目标分量占比一直处于半数以下,有效地解决了算法失效的问题,但仍不能一直保持高概率地得到目标分量;Grover[6]将原算法的固定相位π改变成固定相位,从而使得整体得到目标分量的概率得到了提升;Younes等[7]利用局部扩散算法来改进Grover算法,使得最低成功概率提高至84.72%;Li等[8]提出新的相位匹配条件,使得当目标分量占比超过1/3时,一次迭代就能达到高于25/27的成功率;Zhong等[9]将相位定为1.018,算法可以将成功概率保持在93.43%以上;Li等[10]将旋转相位改为0.1π,使得算法的成功率高于99.38%;Younes[11]后续又把旋转相位改为1.926 84π,新算法的成功概率至少为93.58%;Ma等[12]提出一种在四个相位上都改变的算法,一次迭代时,算法使得在目标分量占比高于1/3的情况下获得97.82%以上的成功率;李盼池等[13]在目标分量占比超过时自适应地算出相位旋转角度,使得改进的算法在这样的情况下能以概率1得到目标分量,但当占比小于时,仍然采用Grover算法,此时的成功率等同于Grover算法。
美中不足的是,以上的改进策略都只能在目标分量占比已经确定的情况下实施,但求解目标分量占比也需要不少的运算。针对这个问题,朱皖宁等[14]提出了一种迭代次数自适应量子搜索策略,该策略在目标分量占比未知的情况下也可以顺利地进行量子搜索。虽然这个算法可以在目标分量占比未知的情况下自适应地停止算法,但Grover算法存在的部分效率低下和目标分量占比过半时的失效问题并没有在该算法中得到改善。
本文主要研究内容是:(1)改进迭代次数自适应Grover算法;(2)将改进的算法来仿真计算粗糙集的核属性。仿真结果表明,改进的算法有效地解决了之前算法部分效率低下和失效的问题。
2 基础知识
2.1 Grover算法
Grover算法主要是由酉变换反复迭代多次组成,其简要示意图如图1。

图1 Grover算法示意图
如图1所示,搜索空间为N,n为量子比特位个数,n与N满足关系N=2n。G算子包含Ga和Gs两个子算子。Ga算子可以实现对目标分量进行相位取反操作。Gs算子在目标分量取反以后再对所有分量进行均值翻转。在特定次数内,逐次迭代G算子,目标分量的概率幅将不断增大。
2.2 迭代次数自适应Grover算法
Grover算法是建立在目标分量占比已知的假设上。但实际问题中,目标分量占比也是需要去求解的。朱皖宁等[14]提出的迭代次数自适应Grover算法在目标分量占比未知的情况下也能求解出目标分量。
迭代次数自适应Grover算法利用了Grover算法的几个特性:(1)Grover算法在迭代合适次数的酉算子后能够首次达到峰值;(2)用于迭代的叠加态总相位和首次变为负值时,目标分量的概率幅首次达到最大值;(3)叠加态分量Z基下相位和正负性由X基下的++…+分量相位正负性所决定。
根据上述几个特性,在每次迭代G算子时,都在Ga算子后面加一个Phase门来测量叠加态的总相位。若总相位为正,继续迭代G算子;若总相位为负,则停止迭代G算子,然后对得到的叠加态进行测量。该算法改进的G算子简要示意图如图2所示。

图2 改进G算子示意图
在目标分量占比未知的情况下,迭代次数自适应Grover算法实现了迭代次数的自主控制。但该算法依然存在着两个比较明显的缺陷:一方面,该算法并没有解决目标分量占比过半时的失效问题;另一方面,算法最终获得目标分量的概率在某些情况下并不是很高。针对出现的这两个突出问题,该研究提出一种改进策略,同时解决了失效和目标分量概率不高的两个问题。
3 改进的量子搜索算法
用经典算法搜寻一个搜索空间中目标时,目标的占比越低,则意味着得到目标的概率越低。而在用Grover算法搜索时,目标的占比越低,反而得到目标的概率越高。利用Grover算法的这个特性,扩大搜索空间的方法可以用来改进迭代次数自适应Grover算法。下面提出并证明几个定理,然后给出改进算法。
3.1 定理及证明

由公式(1)可以看出Tpft并不能保证每次都为整数,而非整数次的迭代次数在现实中是不可能实现的。Grover算法通过对Tpft四舍五入取整来确定算法的迭代次数T。下面基于Tpft提出几个定理。
定理1T值相同的情况下,当Tpft-floor(Tpft)=0.5时,经过迭代算子作用后,叠加态中目标分量的概率幅达到极小值(floor()函数为向下取整函数)。
证明 在Hilbert空间里,设初始等权重叠加态矢量与目标分量值平面垂直矢量的夹角为那么,经过迭代算子作用后的最终叠加态矢量与目标分量值平面垂直矢量的夹角ω=(2T+1)θ。另,根据Tpft和θ的公式可知,当Tpft越大时,ω的值就越小。
当T值相同,且0 由此可以得出当Tpft-floor(Tpft)=0.5时,目标分量的概率幅为极小值。 证毕。 定理2目标分量概率幅的极小值随着T值增加而增大。 证明 定理1已经证明当T值相同且Tpft-floor(Tpft)=0.5时,目标分量的概率幅达到极小值,此时T=Tpft+0.5。在出现极小值的情况下,结合公式(1)及可得出,Hilbert空间中初始叠加态与目标分量值平面垂直矢量夹角为那么最终叠加态与目标分量值平面垂直矢量的夹角则为其中T为正整数。由此得出,T值越大,则ω的值就越接近ω<π),即目标分量的概率幅值sinω就越大。 证毕。 设搜索空间有N个分量,其中目标分量的个数为M。根据上一节提出的定理,新算法将搜索空间增加至4N,这样就可以保证目标分量占比恒小于该研究提出的改进迭代次数自适应量子搜索具体步骤如下: (1)制备n+2量子位的等权重叠加态,其中N=2n。 (2)迭代Ga算子。 (3)测量Phase门,若相位因子为正,顺序执行;否则,跳转至步骤(6)。 (4)迭代Gs算子。 (5)跳转至步骤2。 1973年英国Pugh等人改良的Child分级方案迄今一直被采用Child分级[8]是对肝脏储备功能评估的判定。有研究者等[9]认为Child分级标准是用来评价肝硬化患者肝脏储备功能,可将患者病情程度量化评估,将肝硬化患者的5个指标:一般情况、腹水、血清胆红素、血清白蛋白浓度、凝血酶原时间,按不同状态分三个层次,以1,2,3分记,将三个层次得分相加,视得分情况分A、B、C三级,得分越高说明肝脏储备功能越差。 (6)测量最终的叠加态。 粗糙集的核属性求解问题与量子搜索算法解决的无序数据库搜索问题有很大的相似。因此,将改进算法应用于粗糙集核属性的求解问题上。下面简单介绍一下粗糙集核属性的概念,再给出基于改进量子搜索的求核算法。 粗糙集理论[15]于1982年由Pawlak提出,是一种刻画不完整性、不精确性、不完备性的数学理论。在粗糙集理论中,核属性是至关重要的概念,是粗糙集属性约简的运算核心。下面给出粗糙集核属性的定义。 设S=(U,A,V,f)是一个粗糙集,对于任意属性子集B⊆A,IND(B)表示由B确定的二元不可分辨关系。那么,对于∀a∈A,如果IND(A-{a})=IND(A),则可以认定a在A中是多余的属性(或称为非核属性);否则,称a是A的必要的属性(或称核属性)。 要将改进量子搜索应用于求核问题,先要增加原粗糙集的属性列数,再者就是要改进Ga算子中的判别函数。 4.2.1 增加属性列 设粗糙集S=(U,A,V,f),A中属性列数正好为N。在改进量子搜索的求核算法中,将粗糙集S扩大为S′=(U,A+C,V,f),对于 ∀c∈C ,存在 IND(A+C-{c})=IND(A+C)=IND(A),且C中的属性列数为3N。那么,此时属性列数就正好满足改进量子搜索算法中4N的要求。 4.2.2 Ga算子改进 Grover算法中Ga算子首先实现一个函数功能 f(x)判别目标分量是否为要搜索的值。当判别函数判定是要搜索的值时,f(x)=1;否则,f(x)=0。然后再将区分出来的目标分量进行相位取反。 求核问题中将原Ga算子改为G'a算子,相应地判别函数f(x)改为判别函数f′(x),使其满足如公式(2)所示功能: 4.2.3 算法描述 设粗糙集S=(U,A,V,f),A中属性列数正好为N。基于改进量子搜索的求核算法具体步骤如下: (1)通过增加不改变原分类关系的属性集,得到S′=(U,A+C,V,f)。A+C中的属性个数正好为4N。 (2)制备n+2量子位的等权重叠加态s,其中中的4N个分量分别对应S′中4N个属性列。 (3)迭代G'a算子。 (4)测量Phase门,若相位因子为正,顺序执行;否则,跳转至步骤(7)。 (5)迭代Gs算子。 (6)跳转至步骤(3)。 (7)测量最终的叠加态。 仿真实验将改进算法、Grover算法和文献[14]的算法都来进行对粗糙集的核属性求解,选取的数据集为UCI数据集,选取的平台为Matlab。仿真实验的结果充分说明了改进提出算法的有效性和优势。 实验选取的数据集为UCI数据集,具体数据集的情况如表1所示。 表1 UCI数据集 5.2.1 测试结果 仿真实验采用的数据集为UCI数据集,详细信息已在表1中给出。由于Grover算法要求待求解分量的个数必须满足2n要求,对于不满足该条件的数据集,采用增加不影响分类划分的属性列来补齐。实验分别用Grover算法、文献[14]算法以及改进算法来求解上述数据集的核属性。然后将对不同算法最终得到叠加态中目标分量的总概率进行了对比。实验结果如表2所示。 表2 UCI数据集实验结果 从表2中可以看出:(1)文献[14]算法未能解决Grover算法失效的问题。(2)在原算法不失效的情况下,文献[14]算法最终得到目标分量的概率和Grover算法一致。(3)改进算法则不存在失效的问题;改进算法得到目标分量概率在大部分情况下优于Grover算法和文献[14]算法。 5.2.2 结果分析 通过UCI数据集的对比实验,改进算法虽然在整体上优于Grover算法以及文献[14]算法,但在某些情况下,获得目标分量的概率反而不如对比的两个算法。下面将各个算法的表现绘制在同一张图上来分析改进算法的优势及劣势。Grover算法、文献[14]算法及改进算法在目标分量占比不同情况下获得目标分量概率分布如图3所示。 图3 目标分量占比与解概率的关系 从图3中可以看出:(1)Grover算法存在目标占比过半失效问题,且当目标分量占比超过1/4时,获得目标分量的概率下降迅速。(2)虽然文献[14]算法不用计算目标分量占比,实现了迭代次数的自适应,但算法在获得目标分量概率上的表现并没有提高。Grover算法存在的失效问题和特定区间性能急剧下降问题在该算法中并没有得到改善。(3)整体来看,改进算法不存在失效问题,且获得目标分量的概率总能保持在85%以上。虽然在一些小区间内,改进算法的效率不如Grover算法和文献[14]算法,但在这些区间内算法的效率只是略低于两个用于比较的算法。 本节对提出的改进算法和已有的两种算法进行了对比实验。从实验中可以得出,改进算法不仅实现了迭代次数的自适应,且在整体表现上优于已有的两种算法。 量子搜索算法的一个难点在于目标分量占比的确定,而目标分量占比是许多量子算法用来计算算法迭代次数和相位角度的重要参数。学者提出了迭代次数自适应的算法有效地绕过了求解目标分量占比的问题,但在获得目标分量概率的表现上并没有任何提升。改进的基于迭代次数自适应量子搜索,通过扩大搜索空间,有效地提高了迭代自适应量子搜索获得目标的概率。 不足之处在于,虽然在整体上表现良好,该研究在某些区间里会出现效率略低于对比算法的问题。因此,未来的研究将致力于进一步提升算法的性能。3.2 改进算法描述
4 改进算法在求核属性上的应用
4.1 粗糙集核属性
4.2 基于改进量子搜索的求核算法

5 仿真实验
5.1 数据集
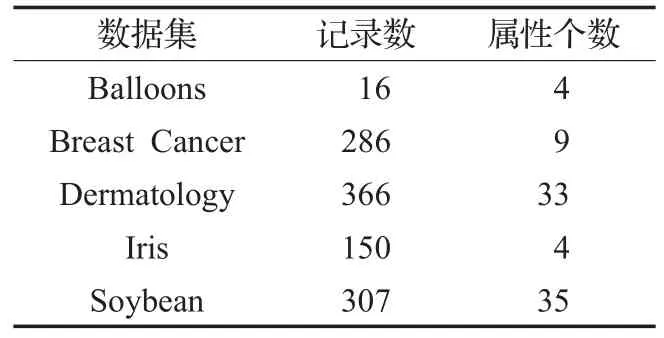
5.2 测试结果及分析


5.3 小结
6 结束语

