非均匀偏振光束在海洋湍流中的光强特性

张艳红，卢腾飞，刘永欣*，陈子阳，孙顺红

（1.华侨大学 信息科学与工程学院 福建省光传输与变换重点实验室，厦门361021；2.漳州城市职业学院，漳州363000）

引 言

近年来，各类光束在海洋湍流中传输的特性因其在水下光通信等领域的潜在利用价值而受到普遍的关注。2011年，KOROTKOVA等人采用一种由温度和盐度共同组成的综合模型的能谱来描述海洋湍流，研究了海洋湍流对高斯-谢尔模型电磁光束的偏振度和光谱的影响［1-2］。随后，国内各研究者也逐渐展开了一些列激光束在海洋湍流中的传输的研究［3-16］。2014年，浙江大学ZHAO等人先后研究了海洋湍流对径向偏振光束、电磁涡旋光束以及电磁非均匀相干光束的传输特性的影响［5-7］。2015年，HUANG等人研究了海洋湍流对部分相干厄米-高斯线列阵光束的光束质量的影响［11］。2015年，XU等人研究了部分相干平顶（partially coherent flat-topped，PCFT）光束阵列在海洋湍流中的传输特性［12］。2016年，大连海事大学LIU等人研究了径向相位锁定部分相干洛伦兹-高斯阵列光束在海洋湍流中的演化特性；2017年研究了部分相干洛伦兹高斯涡旋光束在海洋湍流中的传播特性［15-16］。2018年，西安电子科技大学NIU等人研究了相位屏法模拟高斯阵列光束海洋湍流传输特性［17］。

而当线偏振的激光通过激光放大介质时，温度导致的双折射将对光束的不同部分进行不同的偏振调制，这将导致光束的不同部分呈现出不同的偏振态。这种光束被称作非均匀偏振光束［18-20］。非均匀偏振光束在现实中有很多实际运用，因此研究其在海洋湍流中的传输特性非常有必要。本文中重点讨论了光束参量及海洋湍流强弱对非均匀偏振光束的光强分布的影响。

1 理论推导

假设一非均匀偏振（nonuniform ly polarized，NUP）光束在光源平面的场可以表示为［18］：

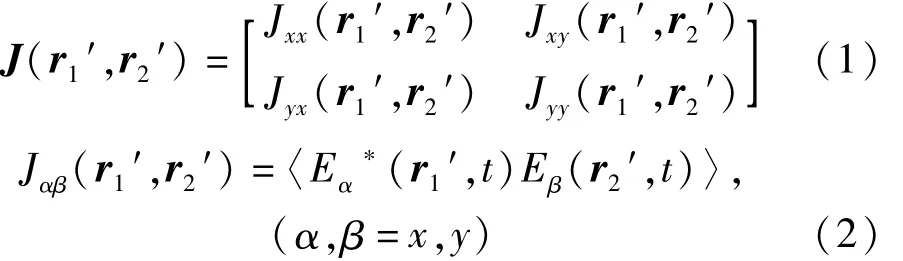
式中，r1′，r2′是光源平面的位置矢量，Ex（r′，t），Ey（r′，t）是场的直角坐标分量，*表示复共轭，〈〉表示系综平均。本文中采用参考文献［21］中非均匀偏振光束的场的直角坐标分量为：

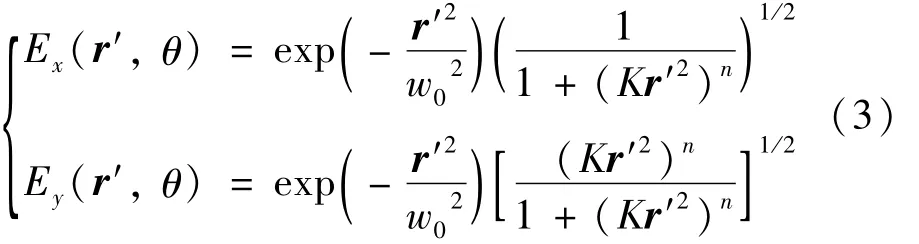
式中，w0代表光束束腰半径，K是比例系数，n是幂指数，K和n会影响非均匀偏振光束的偏振度分布。图1是非均匀偏振光束的初始光强分布及对应的偏振态分布。光束参量分别为w0=1×10-2m，K=4/w02，n=2。

当此光束在海洋中传输时，根据广义的惠更斯-菲涅耳原理，利用源平面的交叉谱密度矩阵元可得到在海洋湍流中传输到Z=z平面的交叉谱密度为［7］：

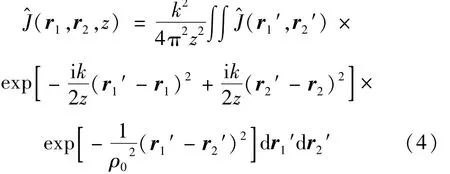
式中，k=2π/λ是波数，λ是波长；r1，r2是 Z=z平面上两点的位矢；ρ0是球面波在海洋湍流介质中传播后的相干长度，其表示为：

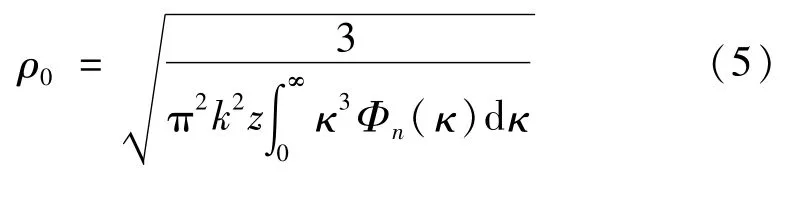
式中，κ为空间频率。

本文中所采用的湍流折射率波动的空间功率谱函数Φn（κ）是基于海洋湍流是均匀各向同性的假设，它可以用下式表示［21］：

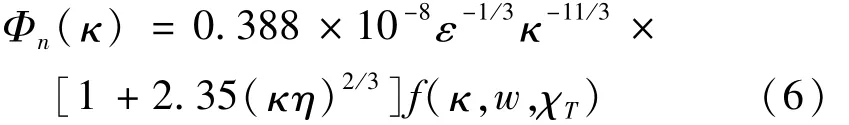
式中，ε是单位质量液体中的湍流动能的耗散率，取值可以从10-4m2/s3～10-10m2/s3，η=10-3m是 Kolmogorov微尺度（内尺度），f（κ，w，χT）可以表示为［19］：

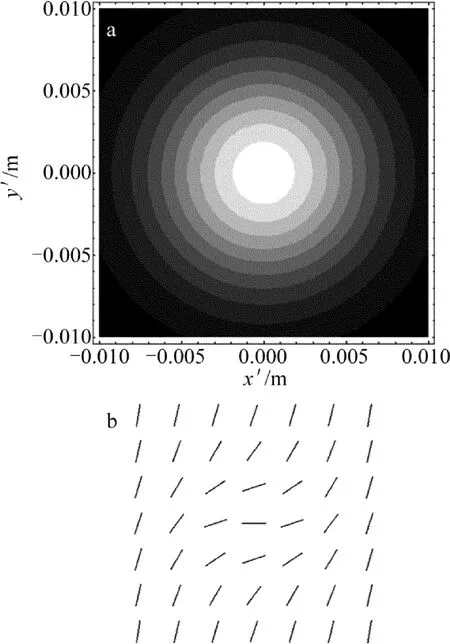
Fig.1 a—the initial intensity distribution of a non-uniformly polarized beam（w0=1×10-2m，K=4/w0 2，n=2） b—the corresponding polarization distribution

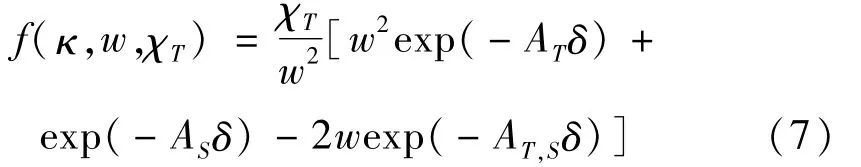
式中，χT是均方温度耗散率，AT=1.863×10-2，AS=1.9×10-4，AT，S=9.41×10-3，δ=8.284（κη）4/3+12.978（κη）2，w是温度和盐度波动的相对强度，其在海洋中的取值为-5～0。

为计算方便，考虑1维的情况，（4）式可以简化为：

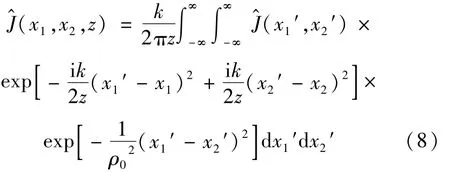
根据（8）式，可以得到光束在输出平面的光强分布为［22］：

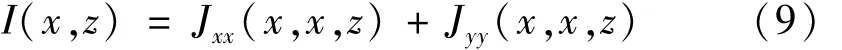
2 数值模拟与讨论

利用数学软件对上述结果进行数值模拟，计算得到图2～图6的结果。如无特殊说明，计算参量为：w0=1×10-2m，K=4/w02，n=2，λ=0.633mm，ε=10-7m2/s3，χT=10-9K2/s，w=-2.5。图 2和图 3是参量n或K选取不相同的数值时，光束相对应的偏振态分布情况。从图上可以看出，当参量n或K取值为零时，光束的偏振态分布为均匀分布。然而当参量n或K选取的数值不为零时，参量n或K发生变化，则光束的偏振态分布也将会发生改变。由此可以看出，参量K和n主要对非均匀偏振光束的偏振度分布产生影响。

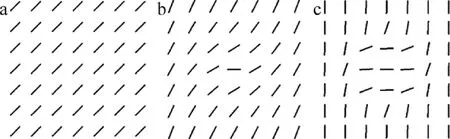
Fig.2 The corresponding polarization distributions of non-uniformly polarized beamswith different parameter n（w0=1×10-2m，K=4/w02）a—n=0 b—n=1 c—n=6

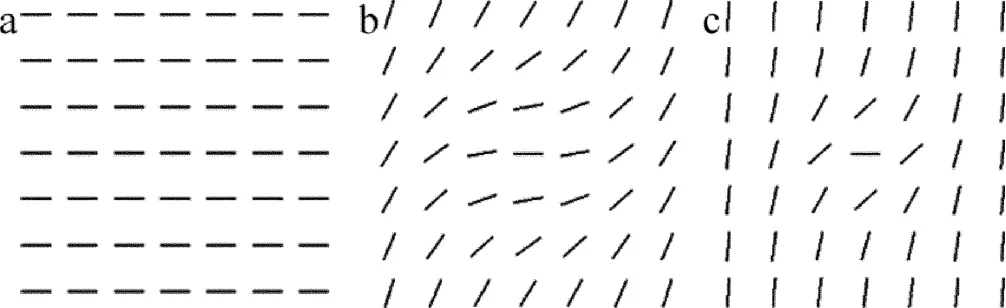
Fig.3 The corresponding polarization distributions of non-uniformly polarized beams with different parameter K（w0=1×10-2m，n=2）a—K=0 b—K=2/w02 c—K=10/w02

图4 中给出了不同n值的非均匀偏振光束在海洋中传播到不同距离时的归一化光强分布。计算参量为：w0=1×10-2m，K=4/w02，λ=0.633mm，ε=10-7m2/s3，χT=10-9K2/s，w=-2.5。由图 4可知，非均匀偏振光束在z=0m处，n取不同值时，光束均为高斯分布。但在海洋中传输较近一段距离后，非均匀偏振光束的光强分布会偏离高斯分布。而随着传输距离的不断增大，在海洋湍流的不断作用下，光源的非均匀偏振特性对光斑的影响越来越小，最后变得可以忽略，光强分布又回到高斯分布。同时也可以看出，当n=0时，光束在海洋湍流传输的过程当中，其归一化光强分布将一直维持高斯分布。

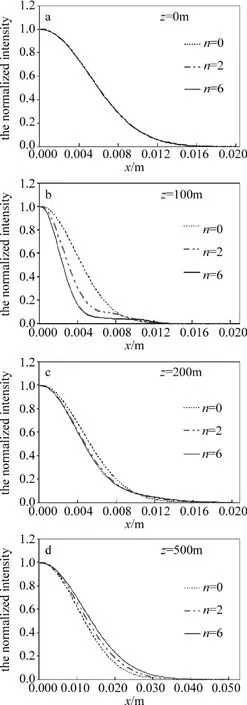
Fig.4 Normalized intensity of non-uniformly polarized beamswith different parameter n at several propagation distances passing in the oceanic turbulence

图5 中给出了不同K值的非均匀偏振光束在海洋湍流中传输到不同距离时的归一化光强分布。从图中可以看出，光束在海洋湍流中传输距离较近时，发现随着参量K的增大，其对光束的光强分布影响越大，偏离初始高斯型分布越明显，但这种影响随着传输距离的增大而减小，最后光强分布又回到了高斯分布。同时也可以看出，当K=0时，光束在海洋湍流传播的过程当中，其归一化光强分布将一直维持高斯分布。

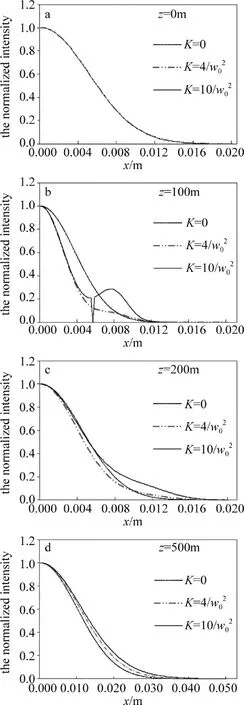
Fig.5 Normalized intensity of non-uniformly polarized beams with different parameter K at several propagation distances passing in the oceanic turbulence

以上的研究为非均匀偏振光束的光束参量对光强分布的影响，下面来讨论各个海洋湍流参量对非均匀偏振光束在海洋湍流传播的过程当中的光强分布的影响。图6为非均匀偏振光束在不同海洋湍流中在传输距离z=100m处归一化光强分布。从图6可以看出，随着χT的增大，ε的减小以及w的增大，非均匀偏振光束的光强分布就会越趋近于高斯分布，也就是说海洋湍流参量对光强分布的影响占主导。

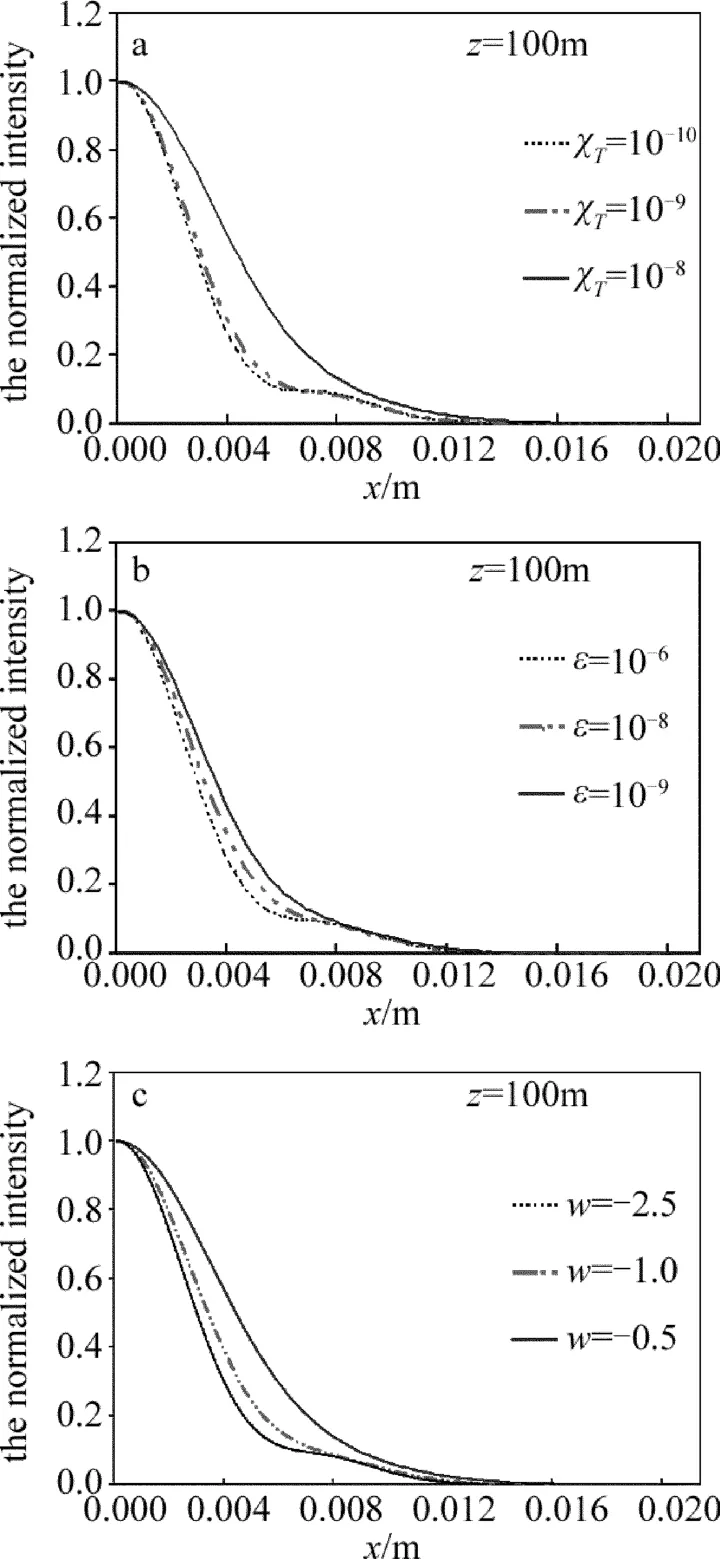
Fig.6 Normalized intensity of a non-uniformly polarized beam（w0=1×10-2m，K=4/w0 2，n=2）propagating in the oceanic turbulence with different oceanic parameters

3 结 论

本文中根据广义的惠更斯-菲涅耳原理，得到非均匀偏振光束经过海洋湍流传输后的光强分布，并对非均匀偏振光束在海水中传播的传输特性进行了详细的研究。数值模拟结果显示，n或K会对非均匀偏振光束的偏振度分布产生影响。当参量n或K选取的值为零时，光束的偏振态分布为均匀分布；而当参量n或K选取的数值不为零时，参量n或K发生变化，则光束的偏振态分布也将会发生改变。由此可以看出，参量n或K主要对非均匀偏振光束的偏振度分布产生影响。当非均匀偏振光束在海洋湍流中传输的距离较近时，发现参量K增大后，其对非均匀偏振光束的光强分布影响越大，偏离初始高斯型分布程度越大。然而，由于传输距离的不断增大，海洋湍流对光束的影响越大，最后非均匀偏振光束的光强分布又回到了高斯分布。此外也发现，随着χT的增大、ε的减小以及w的增大，非均匀偏振光束的光强分布就会越趋近于高斯分布，也就是说海洋湍流参量对光强分布的影响占主导。