一类具有非线性信号产生的趋化性模型解的存在性
孙傲霜
(西华师范大学 数学与信息学院,四川 南充 637009)
生物趋化性是细胞、细菌等生物根据环境中某些化学物质的浓度梯度做出的一种趋利避害的方向性运动,趋化性现象在自然界中普遍存在,其研究不仅能让人们了解到自然界中生物的许多奥秘,同时在生产生活、医疗卫生等方面都有重要作用. 因此,生物趋化性引起了学者们极大地研究兴趣.
上世纪70 年代,美国应用数学家提出了著名的Keller-Segel 趋化模型用以研究变形虫的趋化聚集行为[1].经典Keller-Segel 趋化模型一个显著特征是:当空间维数n ≥ 2 时,模型的解可能会发生有限时间爆破.由于爆破现象不符合生物实际,没有考虑细胞的增长和死亡,因此,需要对该模型进行修正,各种变体模式也因此应运而生[2-5]. 该模型的第二个特点是化学信号浓度对于细胞密度的依赖关系是线性的,而在自然界中信号对于细胞的依赖关系往往很复杂[6].该模型的第三个特点是信号是由细胞自身直接产生,而在实际的很多生物环境中,信号也有可能间接产生[7].
由以上研究启发,本文主要对以下具有非线性间接信号产生的趋化模型进行研究:
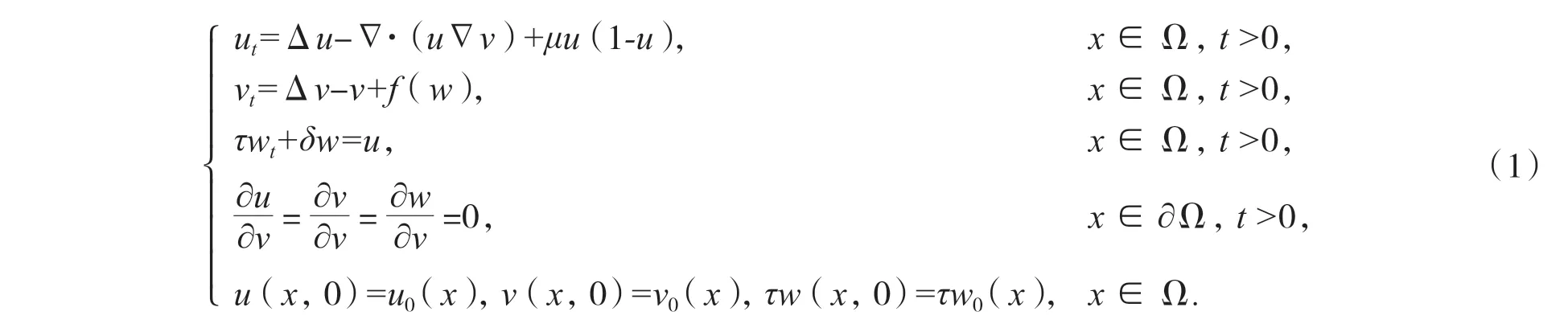
其中Ω⊂Rn(n ≥ 2)是一个具有光滑边界的有界区域,u(x,t)、w(x,t)分别表示飞行的山松甲虫密度和树上的山松甲虫密度,v(x,t)表示树上的山松甲虫分泌的甲虫信息素浓度,μu(1-u)刻画了山松甲虫的增值和死亡,信号v 并不是由飞行的山松甲虫u 产生而是由树上的山松甲虫w 所产生,δ,τ 是正常数.该模型是文献[7]中模型的推广,区别是假设趋化信号v 对于树上的山松甲虫w 的依赖关系不是一般的线性依赖关系,即假设f(s)∈C1([0,+∞))满足:
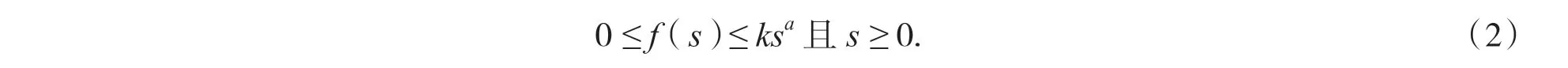
其中k,a 都是正实数,该模型更能确切地描述山松甲虫在自然中分泌信号的现象.本文主要考虑μ=0 的情况下,参数α 对模型解的全局存在性的影响,其实际意义是研究当山松甲虫的增值量和死亡量持平时,树上山松甲虫分泌信号的速率对整个模型的影响,也可用于描述此类型其他物种和细胞的现象.
1 主要结果
定理1 假设μ=0,Ω⊂Rn,n ≥ 2 是一个具有光滑边界的有界区域,和是已知的非负函数,f(w)满足(2),则当:

时,模型(1)存在唯一的非负有界经典解(u,v,w).
2 预备知识
首先叙述模型(1)解的局部存在性,其证明方法与文献[6-7]中类似,本文略去了相应的证明.
引理1(解的局部存在性)设Ω⊂Rn,n ≥ 2 是一个具有光滑边界的有界区域,μ ≥ 0,δ > 0,τ > 0,则对任一的非负初始值(u0,v0,w0)∈C0(Ω—)×W1,∞(Ω)×C1(Ω—),任一的p>n,存在Tmax∈(0,∞)(Tmax表示最大存在时间)使得模型(1)在Ω×(0,Tmax) 上存在唯一的非负经典解(u,v,w)满足:
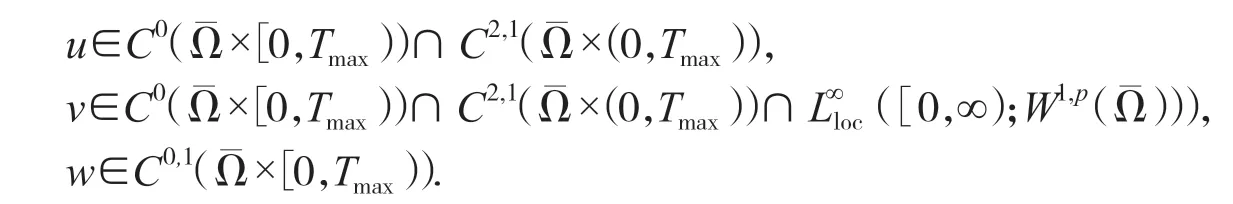
若Tmax<∞,则有
下面的引理2 是非齐次线性方程的正则化性质,可参见文献[8]中的定理4.1、文献[9]中的定理1.
引理2设Ω⊂Rn是具有光滑边界的有界区域,T >0,考虑抛物方程的初边值问题:
假设v0∈W1,∞(Ω)且存在常数C1>0 使对任意t∈(0,T),都有‖f(·,t)‖Ls(Ω)≤C1,其中s ≥ 1.则存在正常数C2(q),对于任意t∈(0,T),该方程的解都满足:

接下来建立u,w 的L1估计.
引理3(建立u,w 的L1 估计)假设μ=0,δ > 0,τ > 0,且u0∈C0(Ω—)和w0∈C0(Ω—)和都是非负的,则对于所有的t∈(0,Tmax),有:
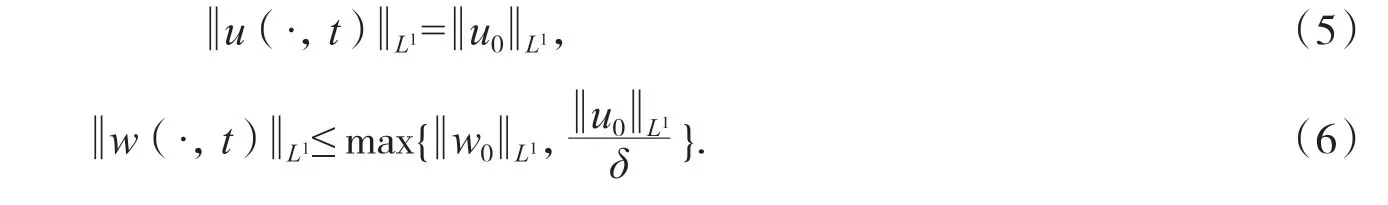
证对(1)中的第一个方程关于x 在区域Ω 上进行积分,利用散度定理可得:再利用齐次Neumann 边界条件(即x∈Ω,t>0),可得到,因此推出(5).
3 定理证明
引理4假设是一个具有光滑边界的有界区域和w0∈C1(Ω—)是已知的非负函数,并且假设0<α<则存在常数C>0,使对∀t∈(0,Tmax),模型(1)的经典解都满足:

证首先断言存在q>n 和c1:=c1(q)>0,使得:
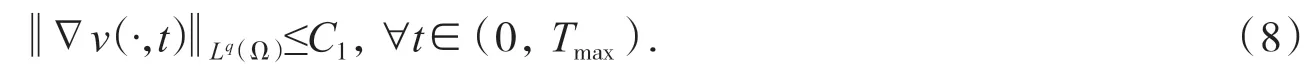
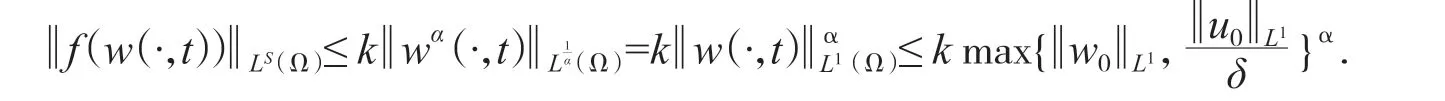
接下来利用文献[10-11]中所用方法证明(7). 由(8)可找到r 满足n<r<q 和使得:
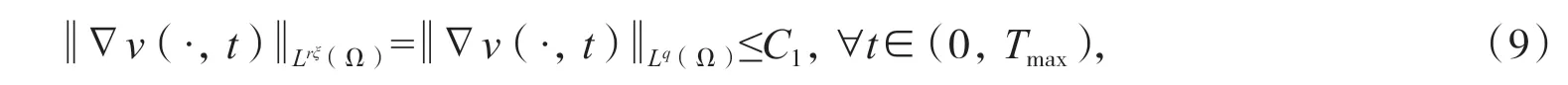
由引理1 不难发现,B(T)是有界的.下面证明B(T)并不依赖于T.首先利用常数变易法,得到:
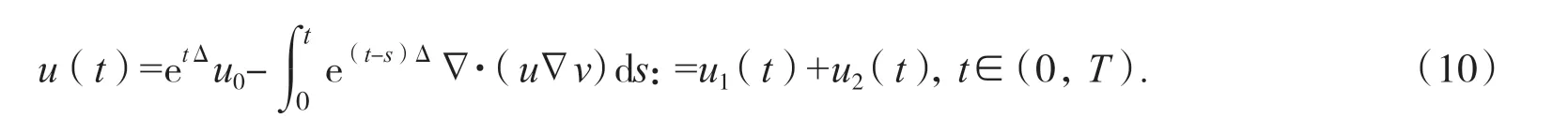
由极大值原理,存在C2>0 且不依赖于T,使得:
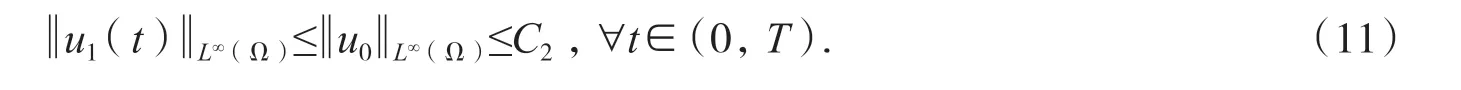
为了估计u2(t)的L∞模的上界,假设λ1是-△在Neumann 边界条件下在x∈Ω 中的第一非零特征值,对任意p∈(1,∞),A 表示-Δ+在空间LP(Ω)中的形式.则对任意θ∈(0,1),A 有分数幂Aθ.由文献[11]中的定理1.3 和2θ->0 可知:

对∀t∈[0,T]都成立,其中C3,…C6是不依赖于T 的正常数.需要进一步估计(12)中最后一个积分.为此,假设ξ':=利用Hölder 不等式有由于r>1 和ξ'>1,利用插值不等式不难得到其中从而进一步得到:
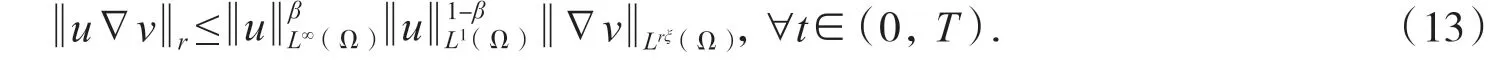
再结合引理2 和(9),即得:
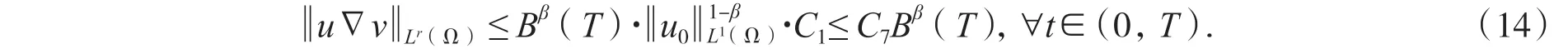
其中C7:=C1‖u0‖ . 综合不等式(10)~(14),可得C8:=max{C2,C6,C7}>0 和C8>0 满足:
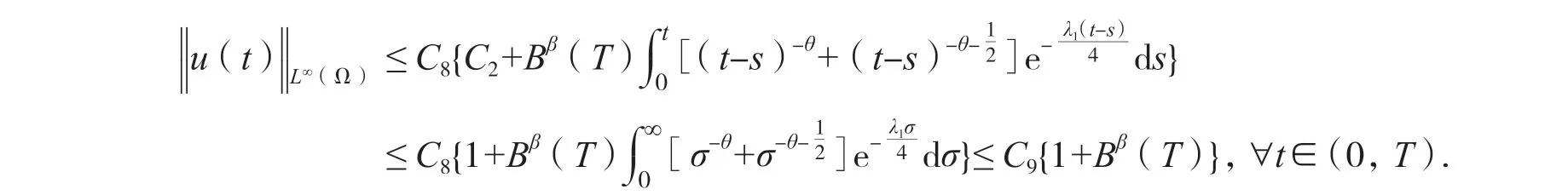

由于0<β<1,由杨式不等式不难得到对于常数C10>0,有结合(15)得到B(T)≤ 2C10.因此‖u(·,t)‖L∞(Ω)≤ 2C11,∀t∈(0,Tmax),则证得引理3.
定理1 的证明:由引理4,再结合引理1 中解的延拓准则,即得Tmax=∞.这就得到了在Ω×(0,∞)上模型(1)的解具有全局存在性和有界性.

