环R+vR 上的常循环码

王艳萍，李 杰

（宿州学院 数学与统计学院，安徽 宿州 234000）

1994 年，Hammons 等研究二元码，并将其看成Z4码对应Gray 映射下的像，使得环上的码引起编码学者的注意［1］.许多研究学者对有限环产生了很大的兴趣.文献［2］研究链环F2+uF2上的循环码及其一类常循环码的一些性质；文献［3-7］进行了推广，分别研究了对应推广环上的常循环码、负循环码的性质.文献［8-9］研究非链环上，不同长度对应常循环码的结构以及它们所对应的性质.通过构造映射，得出环上的结构.本文先介绍环R+vR（v2=v），给出其幂等正交元，进而建立该环上码与R 上码的关系；其次给出该环上的Gray 映射，研究对应性质；最后给出该环上θ-常循环码的生成多项式与环R 上码的结构的关系.

1 预备知识

令ℜ ＝R+vR，其中v2=v.且R 满足以＜r＞为极大理想，其中rl=0. p＞2 是R/＜r＞的特征.设n=psk，（p，k）=1.令e1=v，e2=（1-v），易知e12=e1，e22=e2，e1e2=0，且＜e1＞={e1a│a∈ℜ}，＜e2＞={e2a│a∈ℜ}是互素的理想，则ℜ ≌＜e1＞⊕＜e2＞.因此，对∀c∈ℜ 唯一表示：c=e1a+e2b 其中a，b∈R.本文规定θ=η1e1+η2e2为ℜ 上的单位，而η1，η2∈R.

定义ℜn→ℜn的θ-常循环置换τ：τ（y0，y1，…，yn-1）=（θyn-1，y0，…，yn-2）.特：θ=1，环上的码为循环的；θ=-1，为负循环码.

定义C 为ℜ 上长为n 的线性码：如果C 是ℜn上的非空子集，且是ℜn的子模.

定义Rn上的θ-准常循环置换σ：σ（a0，a1，…，an-1，a'0，a'1，…，a'n-1）=（η1an-1，a0，…，an-2，η2a'n-1，a'0，…，a'n-2）；称码C 为θ-准常循环码，如果有σ（C）=C；θ=-1，为准循环码.

∀c∈R，wHom其中

引理1设C 是ℜn上的线性码，它的长为n，可定义：

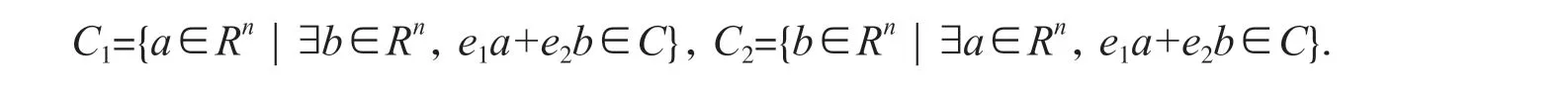
易证：（1）C1、C2为R 上的线性码；（2）C 唯一表示：C=e1C1⊕e2C2.

引理2θ=η1e1+η2e2为ℜ 上的单位⇔η1，η2为R 上的单位.

证“⇒”如果θ=η1e1+η2e2，则必有θ'=η1'e1+η2'e2∈ℜ，η1'，η2'∈R 满足θθ'=（η1e1+η2e2）（η1'e1+η2'e2）=1，即η1η1'e1+η2η2'e2=1，（η1η1'-η2η2'）v+η2η2'=1，所以有η1η1'=η2η2'=1，即证；

“⇐”如果 η1，η2为R上的单位，即∃η1"，η2"，η1η1"=η2η2"=1. 设θ"=η1"e1+η2"e2∈ℜ，因（η1η1"-η2η2"）v+ η2η2"=1，即θθ"=（η1e1+η2e2）（η1"e1+η2"e2）=1，即证.

2 ℜ 上的Gray 映射及常循环码

定义ℜ →R2的Gray 映射φ：对∀c=e1a+e2b∈ℜ，a，b∈R，有φ（c）=（a，b），且是双射.φ 扩展ℜn上，有ℜn→R2n的Gray 映射Φ：对∀c=（c0，c1，…，cn）∈ℜn，ci=e1ai+e2bi，ai，bi∈R，i=0，1，…，n-1，有Φ（c）=（a0，a1，…，an-1，b0，b1，…，bn-1）.定义c 的Gray 重量wG（c）=wHom（a，b），码C 的Gray 距离：dG（C）=min{wG（c）│c≠0，c∈C}，（ℜn，Gray 距离）→（R2n，齐次距离）：保距映射.

定理1设C 是ℜn上的线性码，它的长为n，则C 为θ-常循环码的充要条件，C1为η1-常循环码，C2为η2-常循环码.

证“⇒”对∀（a0，a1，…，an-1）∈C1，（b0，b1，…，bn-1）∈C2，c=（c0，c1，…，cn）∈C，ci=aie1+bie2，则τ（c）=（θcn-1，c0，…，cn-2）∈C，θcn-1=an-1η1e1+bn-1η2e2，则有（η1an-1，a0，…，an-2）∈C1，（η2bn-1，b0，…，bn-2）∈C2，即证；

“⇐”对∀c=（c0，c1，…，cn）∈C，ci=aie1+bie2，则（a0，a1，…，an-1）∈C1，（b0，b1，…，bn-1）∈C2.

又（η1an-1，a0，…，an-2）∈C1，（η2bn-1，b0，…，bn-2）∈C2，则（an-1η1e1+bn-1η2e2，c0，…，cn-2）∈C，即（θcn-1，c0，…，cn-2）∈C，即证.

推论1环ℜ 上的线性码C 是θ-常循环码的充要条件C⊥为ℜ 的θ-1-常循环码；C 是循环码的充要条件C1，C2是R 的循环码.

定理2对上述τ，σ，Φ，有Φτ=σΦ 成立.

证∀c=（c0，c1，…，cn）∈ℜ，ci=aie1+bie2，有τ（c）=（θcn-1，c0，…，cn-2）=（an-1η1e1+bn-1η2e2，c0，…，cn-2），则Φτ（c）=（η1an-1，a0，…，an-2，η2bn-1，b0，…，bn-2）；而Φ（c）=（a0，a1，…，an-1，b0，b1，…，bn-1），又σΦ（c）=（η1an-1，a0，…，an-2，η2bn-1，b0，…，bn-2），即证.

注：由定理2 可知，ℜ 上长为n 的θ-常循环码C⇔Φ（C）为R 上的θ-准常循环码，且长为2n.

定理3［10］设C=e1C1⊕e2C2是ℜ 上的线性码，长为n，则：

（1）C⊥=e1C1⊥⊕e2C2⊥；

（2）Φ（C）=C1⊗C2，│Φ（C）│=│C1│·│C2│；

（3）Φ（C⊥）=C1⊥⊗C2⊥.

证（1）定义：l1⊥={a∈Rn│∃b∈Rn，e1a+e2b∈C⊥}，l2⊥={b∈Rn│∃a∈Rn，e1a+e2b∈C⊥}，则对∀a∈l1⊥，有e1a+e2b=c'∈C⊥，则∀a'∈C1，有e1a'+e2b'=c∈C，且＜c，c'＞=e1aa'=0⇒aa'=0，即有l1⊥⊆C1⊥.另，a∈C1⊥，有c'=e1a'+e2b'∈C⊥满足＜e1a，c'＞=e1aa'=0⇒aa'=0，则证l1⊥=C1⊥.同理可得，l2⊥=C2⊥.即证.

（2）易 知Φ（C）⊆C1⊗C2. 又∀c（a，b）=C1⊗C2，有r=e1a+e2b∈C 且Φ（r）=c=（a，b），即 有C1⊗C2⊆ Φ（C），则Φ（C）=C1⊗C2.而Φ 是双射，则│Φ（C）│=│C1│·│C2│.

（3）由前述可知Φ（C⊥）⊆Φ（C）⊥，Φ 为双射，则│Φ（C⊥）│=│C⊥│=│ℜ2n│/│C│=│Φ（C）⊥│，即Φ（C⊥）⊆ Φ（C）⊥.类似（1）可证Φ（C⊥）=C1⊥⊗C2⊥.

定理4设ℜ 上长为n 的θ-常循环码C，对于C1，C2，如果它们在R［x］/（xn-η1），R［x］/（xn-η2）有C1=（f），C2=（g），其中f，g 首一的多项式，则有C=（e1f+e2g）.

证因C1=（f），C2=（g），则有C=（e1f，e2g）.假设e=e1f+e2g，则e∈（e1f，e2g），即有（e）⊆（e1f，e2g）；又e1e=e1f，e2e=e2g，则（e）⊇（e1f，e2g），即证.

注：上述定理对应于C⊥也有类似结论.

3 结语

本文先介绍环ℜ=R+vR（v2=v），给出其幂等正交元，得出码C 与环R 上码的关系；然后定义了ℜ=R+vR（v2=v）的Gray 映射，研究其性质，并给出了ℜ 上长θ-常循环码C 的生成多项式.本文的研究，可以为后续环上寻求好码提供基础，为编码学提供参考.