基于数字图像的砂岩切削破坏分形研究

李威 ，刘功勋 ，洪国军 ，施绍刚

（1.中交疏浚技术装备国家工程研究中心有限公司，上海 201208；2.航道疏浚技术交通行业重点实验室，上海 201208；3.南京水利科学研究院岩土工程研究所，江苏 南京 210024）

1 概述

随着全球港口建设的逐渐饱和，全球疏浚业正由近岸向深远海拓展。疏浚从近岸走向深远海，面临的首要问题是工程环境的复杂化，疏浚船舶必定要经受挖掘及输送岩石的考验，岩石的疏浚也是疏浚工程的重要难题之一[1]。

提高挖泥船疏浚岩石的能力是疏浚业挺进深远海的前提之一。岩石疏浚过程可分为挖掘及输送两部分，挖掘面临的是能不能挖得动的问题，输送所面临的是能不能运得走的问题。现行挖泥船挖岩施工过程中存在两大主要问题，一是不能较准确地评估刀齿切削过程所受切削力的大小，二是施工工艺参数多根据经验判定，导致切削块体大小不均，大粒径块体在切削过程中容易堵塞刀具，并导致输送过程中管阻增大、磨损严重等一系列问题。

对于能不能挖得动的问题，已有较多学者针对岩石切削开展模型试验[2-4]，探究岩石切削过程中切削力的变化规律及切削力对各参数的响应。对于能不能运得走的问题，首先要研究岩石的切削破碎形态规律，已有较多学者针对岩石冲击、压缩等破坏形式开展试验研究[5-7]，而针对岩石切削破碎形态的研究，虽有学者[8-9]在开展岩石切削模型试验研究切削力的同时对切削碎块进行分析，但所开展的切削模型试验多为小比尺模型，切削碎块较小且多为粉末状，不具有代表性。因此，有必要针对岩石切削开展大比尺切削模型试验，进而研究岩石切削破碎形态与切削工艺参数之间的关系。

分形理论是由法国科学家Mandelbrot[10]创立的，是专门以不规则几何图形为研究对象的计算分析理论。分形理论的创建为岩石破碎的研究提供了新的理论方法，现已广泛运用于岩石力学上，特别在岩石损伤、破碎、块度分析等方面的运用。众多学者[11-14]运用分形理论对岩石不同外力环境下的破碎特征及机理进行研究，也取得了丰富的研究成果。

本文开展了大比尺砂岩切削模型试验，利用高倍数码照相机拍摄切削碎块信息，在此基础上通过图像分析技术结合分形理论对切削碎块块度分布特征进行统计分析。

2 大比尺砂岩切削模型试验

利用疏浚技术装备国家工程研究中心的疏浚过程试验系统进行大比尺砂岩切削模型试验，该试验系统通过台车牵引切削系统进行切削试验，试验切削系统如图1 所示。该切削系统可实现单刀齿在不同切削角度、不同切削深度下的切削试验。

图1 切削系统Fig.1 Cutting system

用于切削试验的岩样为产自云南的均质、细腻、黄色的砂岩，其主要矿物成分为石英、黏土矿物、方解石、长石、铁白云石。切削用砂岩基本物理力学指标如表1 所示。

表1 砂岩物理力学参数表Table 1 The physical and mechanical parameters of sandstone

图2 为切削试验示意图，图中：v 为切削速度；α 为切削角度；d 为切削深度。试验用切削刀齿为尖齿，齿尖宽2.0 cm。为研究切削角度及切削深度对切削碎块的影响，在0.5 cm/s 的切削速度下，选取 40°、45°、50°及 60°作为切削角度，在不同切削角度下开展0.5 cm、1.0 cm 及1.5 cm三个深度的切削试验。

图2 切削试验示意图Fig.2 Diagram of cutting test

在刀齿切入岩石时，齿尖附近的岩石首先会在挤压作用下粉碎成细末，随着刀齿的前进，切削形成较大块碎块，切削过程中碎块如图3（a）所示。切削完成后对切削碎块进行收集，并将碎块过2 cm 筛处理，如图3（b）所示，可见切削产物包括碎屑及较大块的碎块，碎块形状较为一致，总体上呈椭圆状，长轴垂直于刀齿前进方向，且长轴长于刀齿齿尖宽度。

图3 切削碎块状态Fig.3 Cutting fragment status

3 二维数字影像的分形维数计算

3.1 图像处理

将不同工况下切削产物中大于2 cm 的碎块摊铺在白色泡沫板上，利用高倍数码相机，保持镜头的光轴垂直于泡沫板表面对碎块进行拍照，获取碎块原始图像如图4（a）所示。因原图像背景复杂，故利用图像处理软件对原图像背景进行处理，去除原图像背景，仅保留碎块影像，去除背景后的图像如图4（b）所示。提取碎块信息前需对图像进行二值化处理，二值化后的碎块图像如图4（c）所示。图像处理完成后，编写计算程序提取二值化图像中碎块周长及面积数据。

图4 切削碎块图像处理Fig.4 Image processing of cutting fragments

3.2 分形维数的计算

本文分形维数的计算采用Mandelbrot 提出的周长-面积算法，对于岛屿等非规则图形，其周长P 及面积A 存在以下关系：

式中：D 为非规则图形的分形维数。对上式取双对数关系，可得分形公式：

式中：C 为随机变量。对于任意一切削工况下的碎块，通过计算其碎块的周长和面积的对数，建立线性回归模型，所得直线的斜率的2 倍即为该工况对应切削碎块的分形维数D 的值。

图5 为切削角度为50°时，不同切削深度下碎块面积-周长双对数散点图。切削过程中因刀齿在岩石的作用下会向上移动，故实际切削深度与试验方案制定的切削深度略有差异，图5 中所示的切削深度均为实际切削深度，实际切削深度由对切削沟槽的不同位置的深度取点测量后取平均值所得。

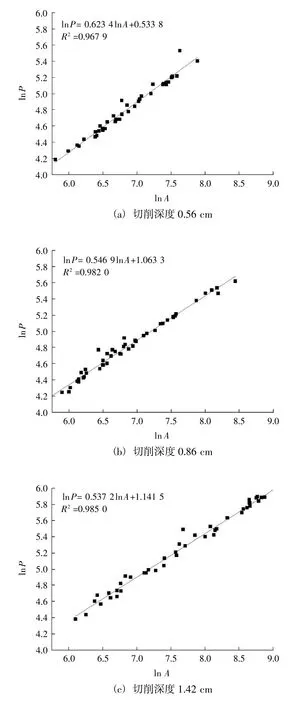
图5 切削角度50°时碎块面积-周长双对数散点图Fig.5 Double logarithmic scatter diagram of fragment area-perimeter under cutting angle of 50°

通过对不同工况下的切削碎块的面积-周长双对数散点图建立线性回归模型可知，每一种工况下切削碎块对应的面积-周长数据均呈现明显的线性相关特征，相关系数均在0.96 以上，说明切削碎块具有明显的分形特征。对不同工况进行统计，可得不同工况对应切削碎块的分形维数，见表2。

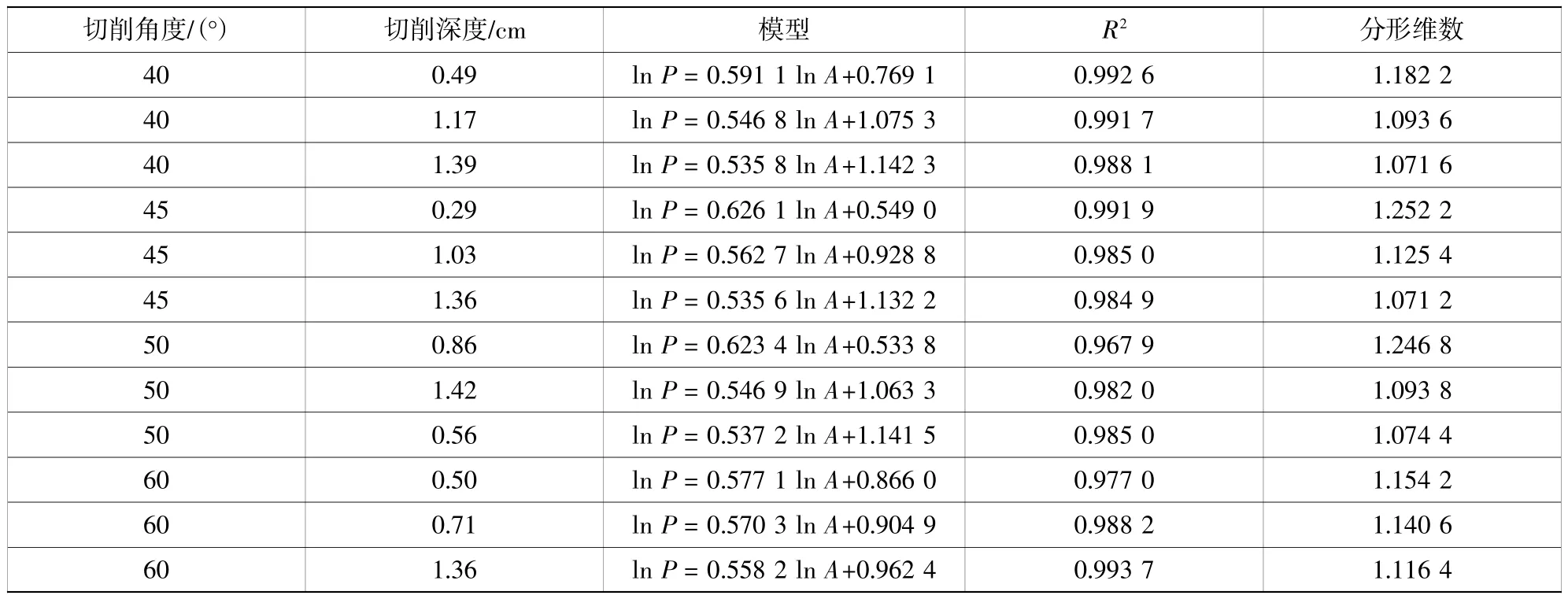
表2 不同切削工况下碎块的分形维数Table 2 Fractal dimension of fragments under different cutting conditions

由表2 可以看出，不同工况切削碎块对应的分形维数不同，但不同工况碎块分形维数均大于1，且集中在 1.07～1.25。

4 切削参数对分形维数影响分析

为分析切削参数对切削碎块分形维数的影响，根据表2 绘制不同切削角度下切削深度与碎块分形维数之间的关系图如图6 所示。由图6 可以看出，不同切削角度下，随着切削深度的增加，切削碎块的分形维数均呈减小的趋势。说明随着切削深度的增加，切削碎块边界趋于更规则。

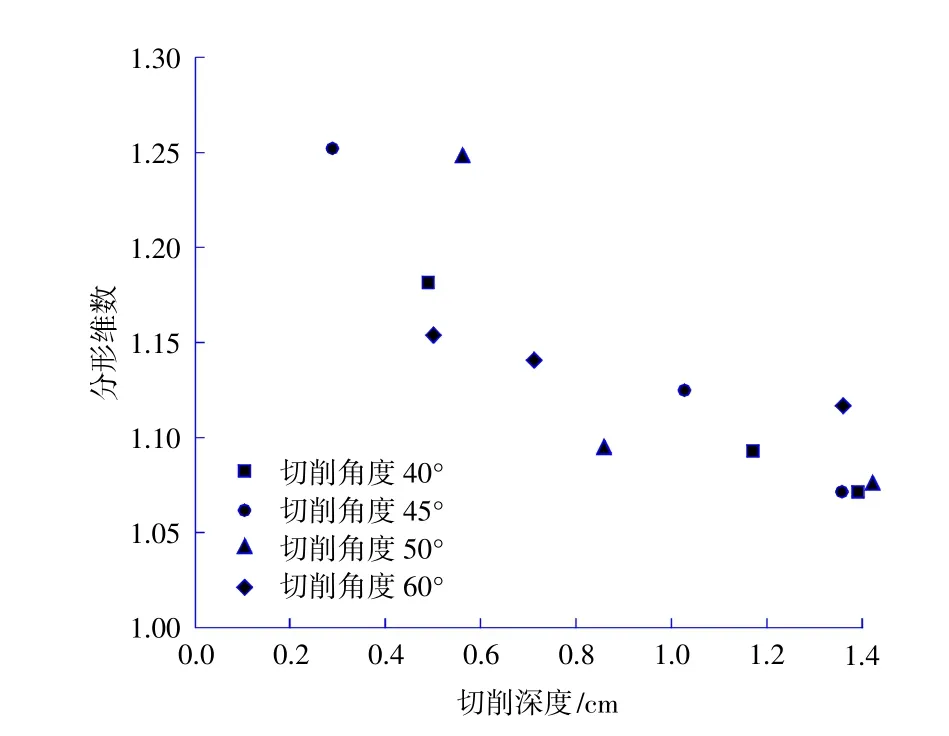
图6 切削深度与分形维数关系图Fig.6 Relationships between cutting depth and fractal dimension

对图6 中不同切削角度下切削深度与分形维数的关系进行线性拟合，拟合结果如表3 所示。通过表3 可以看出，除切削角度50°，其余角度下拟合相关性系数均在0.98 以上，说明切削深度与分形维数之间呈良好的线性关系，两者关系可用一次函数进行拟合。

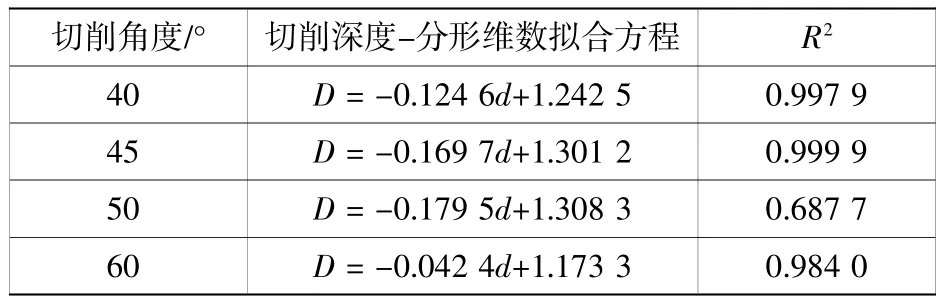
表3 切削深度-分形维数关系拟合结果Table 3 Fitting results of cutting depth and fractal dimension

欲分析切削角度与分形维数之间的关系，需比较在相同切削深度下，不同切削角度的情况。根据表2 可知，实际切削深度与计划切削深度不同，无法直接进行比较分析，需对切削深度进行插值处理。通过分析切削深度与分形维数之间的关系可知，在同一切削角度下，切削深度与分形维数呈线性关系，故利用表3 中拟合方程，分别计算不同切削角度下对应切削深度为0.50 cm、0.75 cm、1.00 cm、1.25 cm 以及 1.50 cm 时切削碎块分形维数。

根据不同切削角度下的不同切削深度对应的碎块分形维数计算结果，绘制切削角度与分形维数之间的关系图如图7 所示。通过图7 可以看出，分形维数随着切削角度的改变而发生变化，且变化规律与切削深度有关。当切削深度较小时，分形维数随着切削角度的增加先增加后减小。随着切削深度的增加，分形维数随切削角度先增加和后减小的速率减小。当切削深度超过1.00 cm 时，分形维数随切削角度的增加先减小后增加。

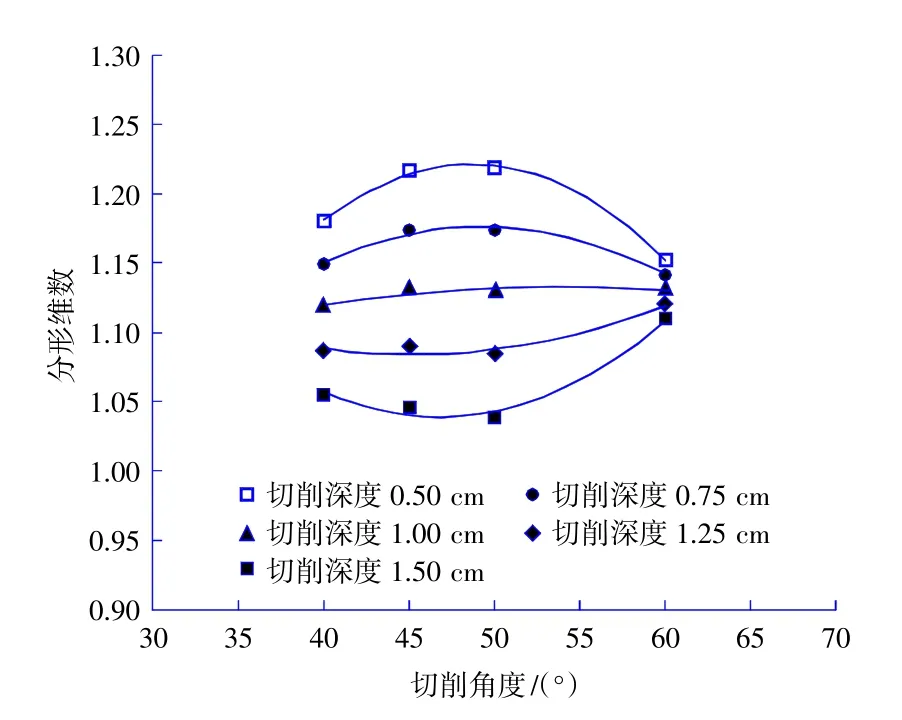
图7 切削角度与分形维数关系图Fig.7 Relationships between cutting angle and fractal dimension

对图7 中不同切削深度下切削角度与分形维数的关系进行拟合，发现通过二次函数进行拟合时，拟合结果与实际结果较为符合，拟合曲线如图7 中曲线所示，对拟合结果进行统计如表4 所示。通过表4 可以看出，除1.00 cm 时拟合相关系数较低为0.76，其余切削深度下拟合相关系数均在0.95 以上，说明切削角度与分形维数之间的关系可通过二次函数进行拟合。

表4 切削角度-分形维数关系拟合结果Table 4 Fitting results of cutting angle and fractal dimension

5 结语

本文开展了大比尺砂岩切削模型试验，利用高倍数码照相机拍摄切削碎块信息，通过图像分析技术结合分形理论对切削碎块块度分布特征进行统计分析，得出以下结论：

1）砂岩切削破碎后的碎块具有明显的分形特征，切削深度在 0.50～1.42 cm，角度在 40°～60°之间时，利用周长-面积算法计算得到的分形维数均大于1，且集中在1.07～1.25 之间。

2）切削碎块分形维数与切削深度及切削角度均有关。相同切削角度下，碎块分形维数与切削深度呈良好的线性关系，两者关系可用一次函数进行拟合，且分形维数随切削深度的增加而减小。

3）分形维数与切削角度间关系较为复杂，不同切削深度下分形维数随切削角度的变化规律不同，但两者关系可用二次函数进行拟合，随着切削深度的增加，二次函数的二次项系数增大，且在一定切削深度下由负变正。