基于台阶法开挖隧道围岩变形的分析与预测

王福和，王树新

（中交第一航务工程局有限公司，天津 300461）

0 引言

近年来，随着国家对基础建设投资的不断加大，以及西部投资发展的需求[1]，西部高速公路和铁路发展迅速，受西部的自然地质条件影响，隧道建设项目会越来越多，尤其复杂地质情况下的长距离大跨径隧道建设[2]，其中有限元仿真计算以及监测数据反演分析为施工的安全建设和运营期的安全运行提供大量的指导。

台阶法开挖适用于软弱地层、第四纪沉积地层、岩层，施工过程中无论地层变好还是变坏，都能及时变换成其他方法，故而被大面积采用和推广，为了保证进度的同时确保工程安全，施工前进行有限元模拟仿真具有重要的作用，从工程参数的选用到实际施工步骤的模拟，以及计算结果的真实性，都将影响工程质量和安全。如何通过前期研究正确及时的对施工过程的安全性进行评价，从而及时消除施工过程的危险点，提出经济的支护建议，控制围岩过大变形，是设计和施工前期必不可少的过程。

韦秉旭和唐辉湘[3]利用FLAC3D 分别模拟湖南某高速公路某隧道在CRD 法与上下台阶法开挖条件下的施工过程，分析隧道开挖过程中围岩的应力、位移及塑性区发展情况，研究两种施工方法对软岩隧道开挖的稳定性影响。于增义[4]依托福建省南平市棋盘石隧道设计与施工，结合当前国内外对隧道施工方法的研究现状，应用有限元软件ANSYS，对棋盘石隧道的施工进行了数值模拟，分析研究了棋盘石隧道在不同围岩类别、不同施工方式、不同施工阶段隧道围岩的稳定性和支护结构的内力、位移特征和变化规律。徐宾宾等[5]针对老鹰山超长破碎带隧道施工，利用有限元软件Plaxis3D 计算分析了开挖过程中隧道的变形情况，着重考虑了围岩等级、开挖方式、双线隧道等对隧道沉降和水平位移的影响。周刚[6]以甘肃省某隧道为例，应用ANSYS 有限元软件，对采用上下台阶法开挖大断面隧道的稳定性进行了模拟分析。然而由于隧道围岩种类多样，施工方法也各不相同，数值计算方法可弥补现场围岩应力测量困难大的问题。本文为分析兰渝铁路龙池山隧道开挖方式、围岩情况对隧道围岩受力及变形的影响开展有限元计算，并将其与监测数据进行对比分析，验证模型的准确性，从而指导设计以及施工。

1 工程概况

兰渝铁路龙池山隧道工程中，开发隧道地质均为II～III 类围岩或节理发育的围岩且围岩开挖断面最大跨度大于13 m，设计采用“台阶法”施工。选取龙池山隧道里程DK458+338—DK458+451 为典型分析区域。该段隧道为IV 级围岩地段，隧道埋深约100 m，围岩主要为千枚岩，隧道高12.9 m，最大跨度约14.7 m，埋深100 m。“台阶法”施工方法，施工、支护顺序见图1。具体步骤为：施作上台阶；上台阶拱部初期支护；开挖下台阶中槽；边墙开挖；边墙初期支护，开挖仰拱，仰拱初支；二衬施作。初期衬砌为曲墙带仰拱，初支采用长度3.5 m，间隔1.2 m（环向）×2 m（纵向）φ22 锚杆； 25 cm×25 cm φ6 钢筋网；厚度为23 cm 的C25 喷射混凝土。为减少台阶之间施工的相互影响，台阶间距60 m 以上，洞身开挖循环进尺按1.5 m 进行。本文将采用数值模拟的手段对围岩变形进行分析，计算“台阶法”围岩开挖施工每一开挖工况下详细的围岩变形情况，评价支护方案，掌握围岩受力状态及分布，提出施工中注意事项。

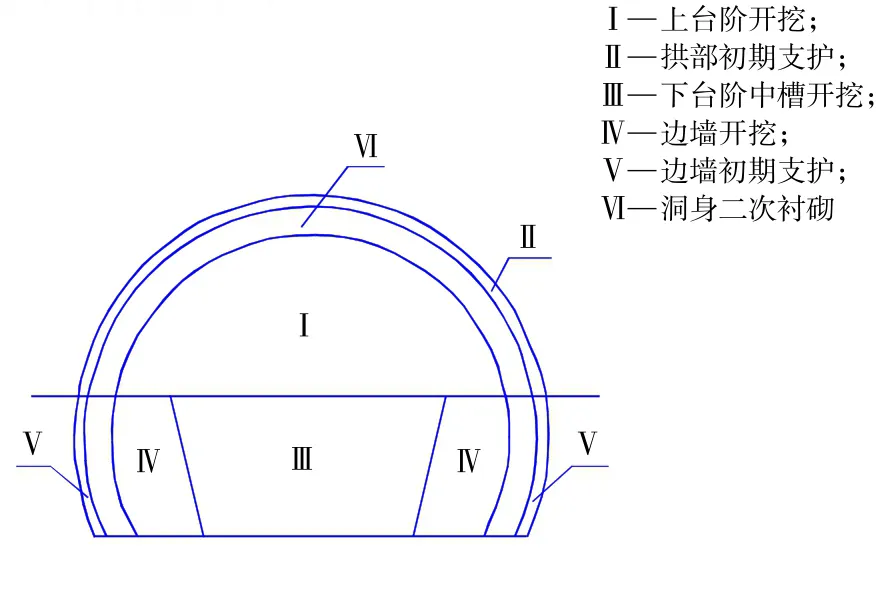
图1 台阶法施工、支护断面图Fig.1 Bench construction and support section drawing

2 模型建立

采用专门用于计算隧道工程的PLAXIS 3D 有限元软件进行建模分析。由于隧道开挖多采用“台阶法”施工，是典型的三维问题，所以建立三维隧道模型，围岩的本构模型采用Mohr-Coulomb模型。

为了便于计算收敛，将初支进行简化，喷射混凝土和钢筋网简化为一层衬砌，锚杆区域则简化为相应围岩区局部加强，采用弹性模型。衬砌与围岩刚性连接。无地下水作用。

施工步骤上只考虑围岩开挖、初支变形情况，对于围岩二衬施工，由于二衬施工时围岩已基本稳定，所以本次分析中不予考虑。数值模拟分析步骤为：根据隧道尺寸及围岩，建立分析模型；参数赋值；定义边界；划分网格；设定初始条件；模拟隧道开挖和支护，分析围岩变形及受力。

根据围岩和衬砌的性质，选择材料参数如表1所示。

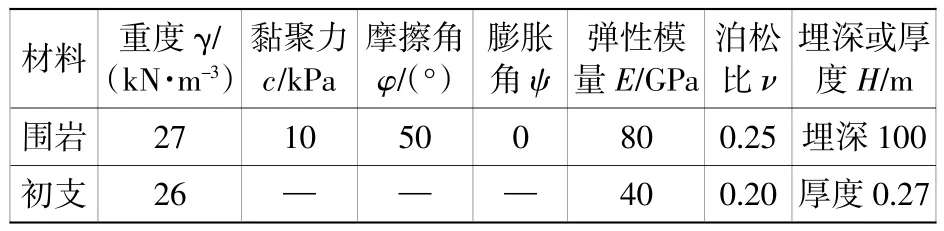
表1 材料参数Table 1 Material parameters

根据隧道实际地层和工程情况建立三维模型，为消除边界的影响，模型左右各向外延伸隧道最大跨度5 倍的距离，下边界向下延伸20 m。上边界为自由边界，无约束，左右边界约束侧向位移，下边界竖向和侧向位移均约束，为固定边界。采用实体单元，网格密度大，计算结果在精度上是可靠的。根据实际开挖的台阶间距和循环进尺，隧道段长度103 m。

3 开挖与支护模拟分析

根据施工顺序，分为4 大步来进行分析计算，1）地应力平衡；2）上台阶开挖和初支；3）下台阶中槽、边墙开挖和初支；4）仰拱开挖和初支。

3.1 上台阶开挖，初支

采用有限元计算，模拟了上台阶开挖、初支的情况。上台阶开挖后立即进行初期支护。

模型计算了上台阶开挖、初支后竖向位移，并由竖向位移可知拱顶沉降、开挖后围岩的整体和断面竖向位移。图2 为加支护后围岩的整体和断面竖向位移图。可以看出，围岩开挖后产生了最大值为7.64 mm 的拱顶沉降，加支护后拱顶沉降速率减小，最终产生7.68 mm 的拱顶沉降。隧道里的围岩由于开挖卸载的作用发生隆起，下部围岩也受卸载作用有隆起的趋势。

图2 隧道支护后拱顶沉降Fig.2 Crown settlement after the tunnel support

数值分析中，空间的总位移值可认为与净空收敛相对应。通过分析可知上台阶开挖、初支后空间总位移、未加支护围岩总位移，最大总位移7.58 mm。图3 为加支护后围岩总位移的整体和断面图，最大总位移为7.62 mm。由图3 可知，由于开挖卸载作用，隧道围岩最大位移仍发生在拱顶位置，说明上台阶开挖拱顶以沉降变形为主，其他两个方向变形很小。而且，围岩变形由拱顶往两侧逐渐减小，隧道内围岩也发生了一定的隆起。初支施工后，围岩发生0.04 mm 的位移，说明初支后围岩逐渐稳定，上台阶净空基本收敛。

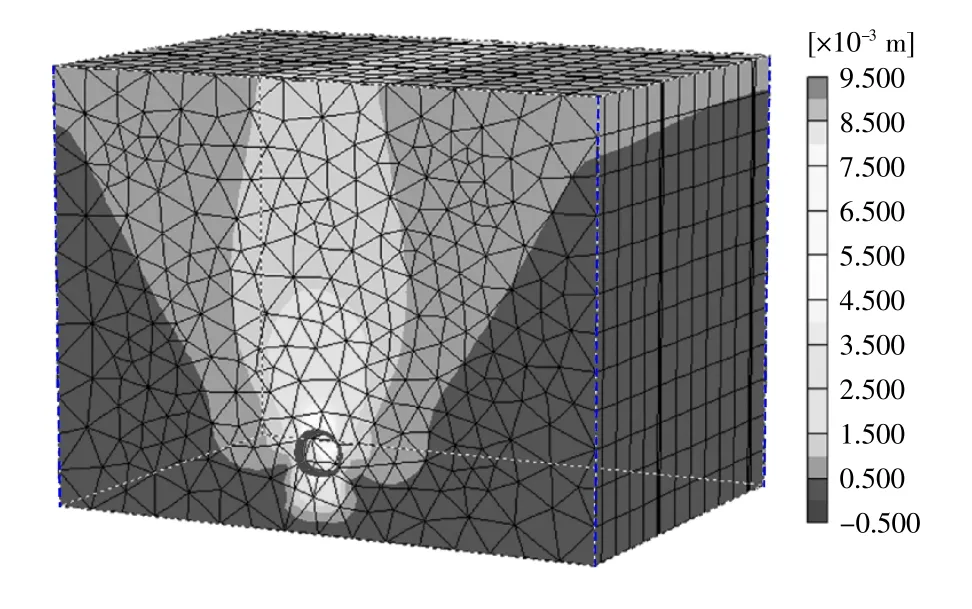
图3 围岩支护后总位移Fig.3 Total displacement after surrounding rock support

计算可得隧道围岩在上台阶开挖、初支作用下的应力分布。可知隧道开挖、支护改变了围岩应力分布，在初支与围岩相接处围岩应力最大，且有应力集中现象，极易在此位置发生破坏或不稳定现象，施工中应注意，并尽快实现围岩支护闭合。

3.2 下台阶中槽开挖，边墙开挖、初支

下台阶施工分为开挖隧道中槽，边墙开挖和初支。上下台阶间距60 m。根据仿真模拟可知下台阶中槽开挖，边墙开挖、初支后围岩总位移。在该工况分析计算中，认为上台阶施工后围岩已稳定，故在净空收敛计算时，将上台阶施工后围岩的位移设为零，单独研究下台阶施工时围岩的净空收敛变形。由边墙开挖围岩总位移仿真分析结果可知由于中槽开挖卸载后，卸载的围岩表面发生最大1.84 mm 的变形。而当边墙开挖、支护后总位移进一步增大，边墙开挖后最大总位移增加到4.55 mm，说明边墙开挖对围岩变形影响较大，初支后为4.56 mm，最大位置在上台阶与下台阶相交的位置。往拱顶和边墙底位置变形逐渐减小，隧道内部的围岩也由于卸载发生一定的隆起。初支后，围岩发生0.01 mm 的位移，说明初支后围岩逐渐稳定，下台阶净空基本收敛。

根据分析可知下台阶中槽开挖、边墙开挖和支护后的围岩应力分布。中槽开挖后，由于边墙位置围岩还未开挖，因此上台阶施工后产生的应力集中现象并未缓解，台阶交接处仍为不稳定位置。而随着边墙的开挖，围岩应力逐步沿边墙向下扩散，应力集中现象缓解，到边墙支护后，应力进一步扩散，已无应力集中。由上分析可知，上、下台阶施工间隔时间不宜过长。

3.3 仰拱开挖，初支

上、下台阶开挖后，即可进行仰拱的开挖和支护，形成支护闭合。

根据仿真模拟可以得到仰拱开挖、支护工况下围岩总位移。同样在该工况分析计算中，认为下台阶施工后围岩已稳定，在净空收敛计算时，将下台阶施工后围岩的位移设为0。由仰拱开挖围岩总位移仿真分析结果可见，仰拱开挖施工对隧道围岩影响较小，由于卸载，围岩发生最大变形仅为0.85 mm，发生在仰拱的中间位置，主要为向上的隆起变形，工程影响较小。仰拱加支护后围岩最大的变形为0.86 mm，相比开挖施工，支护后围岩变形速率较小，围岩只发生0.01 mm的变形。

根据仰拱开挖和支护后围岩应力分布仿真结果可知，仰拱开挖、支护对围岩应力影响不大。由于卸载作用，在隧道底部位置发生一定的应力释放，底部围岩应力减小。隧道两侧应力进一步向隧道底部扩散，使得隧道的应力分布更均匀，隧道支护闭合，围岩已稳定，未见应力集中现象的发生。

4 计算结果与现场监测结果的比较

为了验证模型及参数的合理性，选择典型的断面进行实测数据与计算结果的对比分析。将已形成闭合的断面DK458+378 作为典型分析断面，在该断面数值计算模型上选择与现场测点相对应的测点，给出各个测点在相应时间下的变形值，与现场实测值进行了对比分析，见图4。

图4（a）为围岩拱顶沉降实测值与计算值的对比，可以看出，二者基本相同，前期基本吻合。实测数据在最后的几天，要稍大于计算值，认为是现场复杂的施工环境与数值分析理想的状态之间的差异而引起的误差。由图4（b）可知，上台阶净空收敛的计算值稍大于实测值，二者趋势相同，基本吻合。由图4（c）可知，下台阶净空收敛计算值要大于实测值，实测值下台阶收敛值为0.87 mm，计算值最大为1.1 mm，考虑模型的收敛问题，数值计算中做了一定简化，造成了一定的误差，由于下台阶净空值只有1 mm 左右，所以实测值和数值计算结果之间的差异看上去比拱顶沉降和上台阶收敛的差异要大，实际上其差值仅0.24 mm，在合理范围之内。

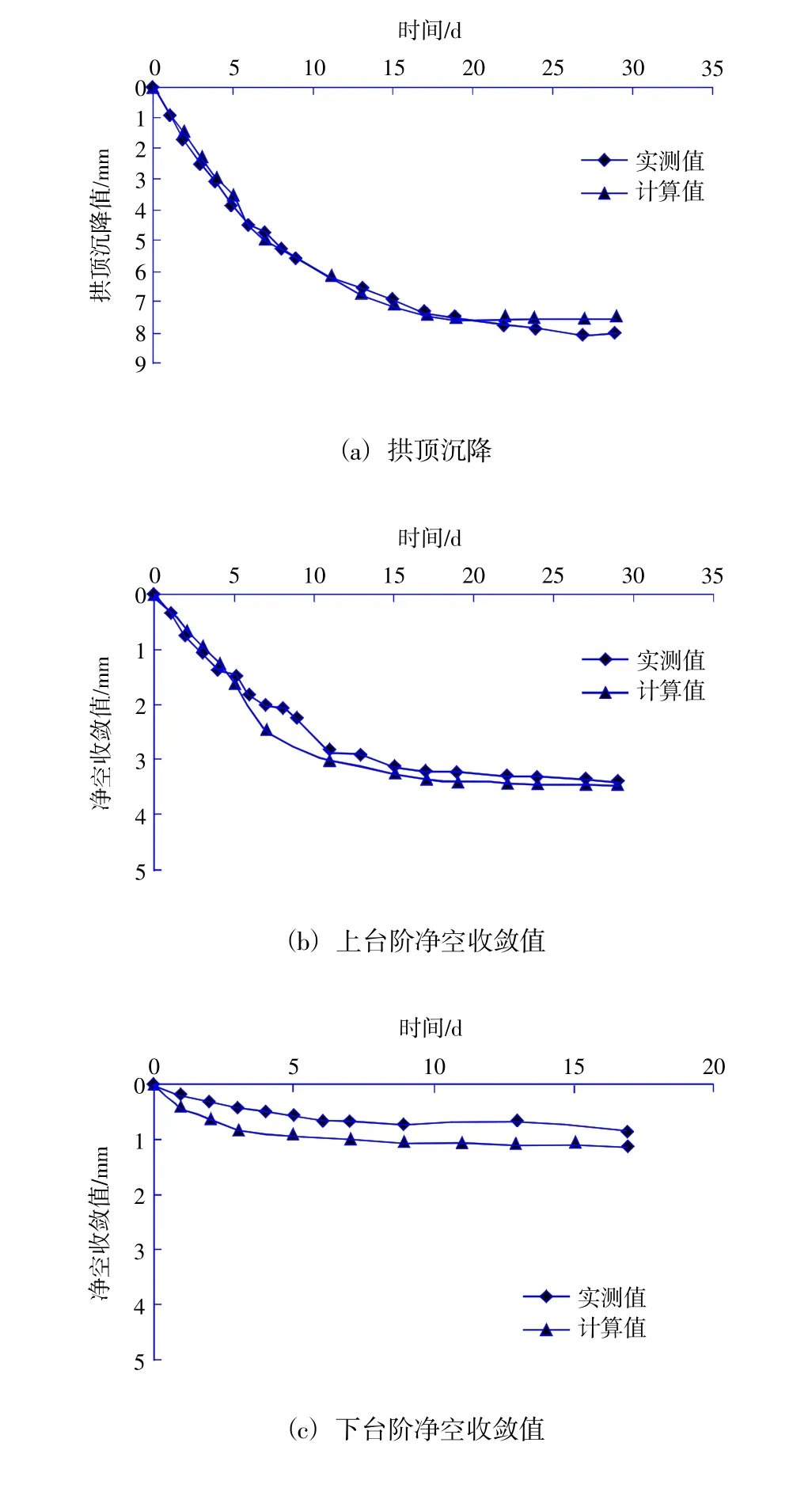
图4 实测数据与计算结果对比Fig.4 Comparison of measured data and calculation results

综上，在不考虑现场复杂施工环境与数值分析理想状态之间差异的影响，数值计算结果与实测值拟合较好，说明计算所采用的模型和参数是合理的，计算的结果也是可靠的。

5 结语

本文以兰渝铁路龙池山隧道为例，建立了3D有限元数值模型，对“台阶法”开挖隧道过程进行了模拟，得出结论如下：

1） 在模拟计算的里程为 DK458+338 —DK458+451 内，采用“台阶法”施工，上台阶开挖、支护后的隧道最大拱顶沉降为7.68 mm，最大的净空收敛值为7.62 mm，下台阶施工完成后隧道最大净空收敛值为4.56 mm，仰拱施工后隧道变形值为0.86 mm；变形均发生在围岩开挖后，加入支护后围岩变形速率减小，围岩逐渐稳定；

2）上台阶围岩开挖、支护施工后，在台阶相接处有应力集中现象，围岩容易发生破坏或不稳定，而在下台阶施工后，围岩应力逐步扩散，应力集中现象逐渐消失，因此，在满足施工要求的条件下，上、下台阶施工间隔时间不宜过长，应尽早进行下台阶施工；

3）通过实测值与数值计算值的对比分析，计算模型及参数合理，结果可靠。相比现场监测，数值分析方法可掌握隧道和周围的围岩整体的变形趋势，更直观全面地了解隧道施工过程中的围岩状态，评价施工方法，提出施工应对措施。而且数值计算可对围岩应力进行分析，弥补现场围岩应力测量困难大的问题。因此，隧道施工中，可将数值分析方法与现场监测方法相结合，达到对新奥法隧道施工更全面的监控；

4） 对于与数值模拟类似的IV 级围岩地段，采用“台阶法”施工是可行的。

综上所述，有限元结果与现场实测结果比较吻合，可有效地指导现场安全施工，本文结果可为同类型施工提供参考。