无锡中考热门压轴题型之翻折类隐圆问题

孙宇

【摘 要】 几何的三种全等变换中（平移、翻折、旋转），翻折和旋转是无锡中考考查的重点。其中，翻折类的变换在近几年无锡中考真题和模拟题中反复出现，让很多学生都难以找到准确方向，本文针对这一类问题，给出最常用、最基本的解答方法。

【关键词】 翻折;中考;隐圆

一、翻折类隐圆问题的提出

翻折是一种全等变换，翻折前后的对应线段和对应角是相等的。由于这样的性质，当沿着同一端点的某条射线进行折叠，那么对应线段之间必然有一个公共的端点。根据圆的定义，我们可以判断，对应线段的另一个端点必然在一个圆上，这个圆就是折叠过程中形成的“隐圆”。下面我们通过典型例题的分析，來充分理解这一类问题的具体含义和求解方法。

二、重点例题详细理解与分析

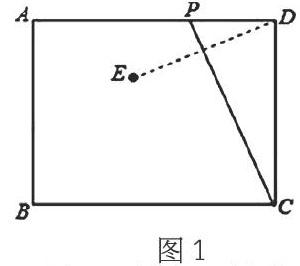
例1：如图1，已知矩形ABCD中，AB=4，AD=m。动点P从点D出发，在边DA上以每秒1个单位的速度向点A运动，连接CP，作点D关于直线PC的对称点E，设点P的运动时间为t（秒）。

（1）若m=6，求当P，E，B三点在同一直线上时对应的t的值;

（2）已知m满足：在动点P从点D到点A的整个运动过程中，有且只有一个时刻t，使点E到直线BC的距离等于3。求所有这样的m的取值范围。

理解分析：这一题是2017年无锡市中考压轴题。该题目的背景设置为矩形的翻折类问题。在矩形的翻折类问题中，我们常用的方法就是如上文所述的勾股定理和“K型”相似。第一问比较常规，连接PB，由翻折的性质可以得到PD=PE=t，由PC为∠DPE的角平分线，AD∥BC，则∠DPC=∠BPC=∠BCP，因此PB=PC=6，即△PBC为等腰三角形）（这里利用的“平行、平分、等腰”的关系，是无锡中考的重点方法之一，在2015年的25题、2018年27题等压轴题中均有相关应用），然后在Rt△ABP中利用勾股定理可以轻松求解。

第二问是我们研究的最重要题型。由题意可得，PD的长即为m的取值范围。由于翻折前后的线段长度不变，即CE始终与CD相等。从而可以确定E点的运动轨迹是以C为圆心，CD为半径的一个圆。理解到这一步，对于题目的最终解答就比较清晰了。画出这个圆，如图2所示，当点E在BC上方，恰好距离BC的长为3时，作垂线，分别交AD、BC于点M、N，由于∠PEC=90°，可以轻松求得PE的长，也就是m的第一个临界点值。当点E到E'位置时，是其第二个距离BC长度为3的时刻。此时E在BC下方，如图3所示，画出辅助线（虚线部分），依然利用“K型”相似即△P'M'E'∽△E'N'C'，可以得到第二个解（也可以利用勾股定理求解，相对而言，“K型”相似计算更加简便）。充分理解第二小问的解题过程，我们发现翻折类的隐圆问题画出动点的轨迹（隐藏的圆）是一个关键的突破口。只要能充分理解到这一点，这一类题目的解答思路就会变得很明晰。

例2：如图4，已知矩形ABCD中，AB=2，BC=m，点E是边BC上一点，BE=1，连接AE。沿AE翻折△ABE，使点B落在点F处。

（1）连接CF，若CF∥AE，求m的值;

（2）连接DF，若≤DF≤，求m的取值范围。

理解分析：这一题是无锡2019年的模拟题。这一题的题目背景和例1几乎一样，问题的设置也有着相似的地方。根据例1的解析方法，首先画出F点的轨迹：以A为圆心，AB为半径的圆。第一问，在此不进行赘述。在第二小问中，设QE=x，由于∠AFE=90°，利用“K型”相似可以得到PF=2x，则FQ=2-2x，在Rt△FEQ中，利用勾股定理求得x=，由此可以求得PD2和PD1的长（D1和D2关于点P对称），从而可以得到最终的m的取值范围（即AD1和AD2的长）。回顾总结这一题的突破点，依然在于这一“隐圆”的重要思路，后续的解答，基本上是很常规方法的使用。

例3：已知平行四边形ABCD中，∠ABC=60°，AB=4，BC=m，E为BC边上的动点，连接AE，作点B关于直线AE的对称点F。当点F到直线BC的距离d满足条件：-2≤d≤+4，求m的取值范围。

理解分析：这一题是2019年无锡模拟试题，我们发现和上面的两道例题很类似，只不过题设的背景变为一个含特殊角（60°）的平行四边形。根据上面的解答思路，我们画出F的轨迹：以A为圆心、AB为半径的圆。如图5，过点A作BC垂线，分别交圆A于点F'，交BC于点H，则AH=，F'H=+4，我们发现，这一长度也是F点距离BC的最大距离。而由题意可知，（如图6）不论m取何值，F点始终在弧BFB'上（不能达到B'），所以这一题的解答就会变得更加清晰：只需要求解最小值的临界点就可以了。过点F作垂线，分别交AD、BC于点P、M，从而得到PF=2，而AP=4，所以∠PAF=30°。后续的解答比较常规，读者可自行探究。

通过以上三道例题的详细分析理解，我们可以充分体会到翻折类问题最大的突破口就在于画出题目中的“隐藏的圆”，让该圆“现出真面目”，这一类题目也就会“现出真思路”。当然在画出圆后的解答过程中，我们的基本功要扎实，“K型”相似和“勾股定理”的运用要相当熟练，另外，翻折是一种几何全等变换，其前后对应的等量关系（对应角和对应线段都是相等的）一定要时刻把握住。数据的处理与分析，也是一个小考验。对于压轴题的理解与分析，要注重数学方法运用，不能过于关注“述”，而轻视“法”、忽略“道”，才能真正做到一通百通。

【参考文献】

[1]董磊.数学思想方法的价值和意义[J].中学数学教学参考（中旬），2018（10）：46-48.