基于序列凸优化的多约束轨迹快速优化

杨 奔 李天任 马晓媛

中国运载火箭技术研究院，北京100071

0 引言

再入飞行器利用气动力在大气层内进行长时间、远距离、高马赫数的飞行，期间会受到极其复杂的非线性热流、动压、过载约束以及终端的高精度约束，使其轨迹规划问题成为一个极富挑战性的问题，引起了国内外许多学者的研究兴趣[1]。传统的再入弹道优化设计方法主要有基于极大值原理的间接法和基于非线性规划理论的直接法[2]等优化算法，两者或因巨大的计算量，或因不易收敛，都只适合离线的轨迹优化[3-6]。虽然航天飞机所采用的基于阻力加速度剖面的轨迹规划[7]，曾取得过辉煌的成绩，但该方法的简化过程限制了飞行器的机动能力。总的来说，基于极大值原理的直接法推导最优解的过程较为繁琐，对于复杂问题几乎无法得到解析解；以伪谱法为代表的直接法对多阶段等复杂问题的建模过程比较麻烦；而以粒子群法等现代启发式算法对于计算量大、优化参数多的复杂模型优化问题，需反复交叉、变异、迭代，计算效率较低。

强耦合性、强非线性使得再入轨迹规划问题难以直接求解，通常需要采用一系列易于求解的子问题逼近原问题。凸优化具有多项式复杂度，局部最优解即全局最优解等特点，加上独特的内点法，使得数学上所有易解的规划问题几乎都指向了凸优化[8-9]。美国加州理工大学的文献[10-15]最早开展了基于凸优化的轨迹优化研究。文献[10-11]针对火星软着陆问题最先提出了无损凸化(Lossless Convexification)的概念，使用松弛的凸形式约束代替原非凸约束，将原问题转化为凸问题，并利用极大值原理对二者的等价性进行了证明，保证转化过程的“无损性”。针对具有非凸约束的一般形式线性系统最优控制问题，文献[12-13]讨论了无损凸化的方法，对原问题与凸优化问题的等价性进行了证明。相关理论研究成果已经在NASA的G-FOLD飞行试验中得到了成功应用[14]。

近年来，许多学者都在尝试将凸优化引入到再入轨迹规划问题中来。文献[15]在给定攻角剖面的条件下，通过变量替换得到以能量为自变量的动力学方程，采用序列凸优化解决了再入轨迹优化问题。文献[16]则以时间为自变量，以倾侧角的导数为控制量，求解了终端时间固定的轨迹规划。现有的基于凸优化的滑翔再入轨迹规划方法基本上都直接使用了小扰动线性化来处理微分方程的非线性，同时添加了信赖域约束来保证子问题向原问题逼近。虽然目前的序列凸优化技术简单可行，寻优时间较传统直接法有一定优势，但是在实际仿真计算中还会遇到以下问题：1)反复迭代的序列凸优化技术本质上还是牛顿法，其收敛范围小，并且在迭代后期可能会出现类似与牛顿法的Maratos效应，导致迭代寻优失败。2)当初值给的比较粗糙时，子问题的可行性将是一个严峻的问题，可能出现“伪不可行”[17](artificial infeasibility)的情况使得迭代失败。

针对上述序列凸优化的不足之处，本文提出了几种改善其收敛性的方法。首先通过增加虚拟控制量，可避免迭代初期由于控制能力不足带来的“伪不可行”问题，降低该算法对初始参考轨迹的依赖。其次通过B样条曲线离散控制量，抑制由于离散带来的锯齿化现象。最后，引入一种“回溯搜索”的方法，改善迭代过程中状态量的振荡，从而加快算法的收敛。

1 轨迹优化模型

1.1 再入动力学模型

考虑地球自转的影响，建立如下再入飞行器无量纲运动方程：

(1)

其中，r,θ,φ,V,γ,ψ分别为无量纲化的地心距、经度、纬度、对地速度、航迹角、航向角，地心距按地球平均半径归一化，对地速度按第一宇宙速度归一化。速度σ为倾侧角，无量纲化升力L、阻力D的表达式为

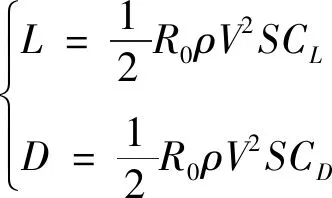
(2)

其中，ρ是大气密度，为简化问题，采用指数形式的大气模型ρ=ρ0exp(-βh)，S为飞行器的气动参考面积，升力系数CL、阻力系数CD均认为是攻角和马赫数的函数。

1.2 基本约束

飞行器再入过程中，为保证飞行任务的成功，需满足热流、动压、过载等路径约束，可表示为

(3)

q=0.5ρV2≤qmax

(4)

(5)

至此，得到该最优控制问题(P1)如下

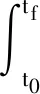
(6)

(7)

(8)

(9)

式(7)中动力学方程可表示为

(10)

其中，第1项是与状态变量相关的项，第2项是与控制量相关的项，第3项是与地球自旋相关项。可以看出，选择倾侧角变化率为控制量，使得控制量与状态量自然解耦，更加有利于优化收敛。

1.3 凸化处理

由1.2节可知，P1是一个高度的非线性最优控制问题，无法直接采用凸优化方法求解。本文采用基于信赖域约束的序列凸优化方法。通过求解一系列的凸优化子问题，逐渐逼近原有问题的解。

将式(10)一阶泰勒展开，由于地球自旋速度较慢，可认为fΩ(x)≈fΩ(xk) ，则线性化的动力学方程为

(11)

其中，

(12)

(13)

为避免迭代初期“伪不可行”的问题，降低对初值的依赖程度，同时弥补线性化带来的误差，在式(11)中增加一个虚拟控制量w，可得

(14)

可在迭代时，在目标函数中控制虚拟控制量的范围，使其在迭代后期为小量，保证问题的准确性。

J′=J+λCw

(15)

2 算法表述

2.1 问题离散

为求解无限维最优控制问题的数值解，必须对其进行离散。为了简单起见，状态变量像通常一样离散成等距的数值点，各个数值点处的控制量则通过B样条曲线控制点的表达式表示，控制点个数的选取可在实际仿真中调整，优化过程中的积分项均采用梯形积分表示。仿真结果显示这种方法可以十分有效地抑制数值求解中控制量的锯齿化现象，更加有利于迭代收敛，并且减少了需要求解的变量个数。将时间N等分，可得离散后的动力学方程。

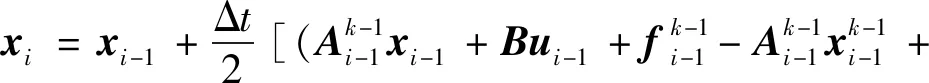
(16)

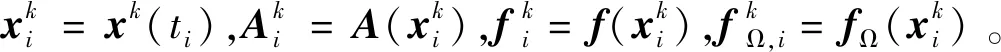
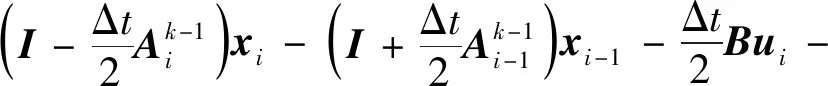
(17)

2.2 回溯搜索

大气层内各个状态变量与控制量相互耦合，具有极强的非线性，且各个约束集也均为非凸，导致无法直接运用内点法进行求解。受序列二次规划算法的启发，国内外学者提出了基于信赖域约束的序列凸优化技术。其信赖域约束是为了保障线性化的可靠程度。当然，每次外层迭代所使用的参考轨迹的不同使得每次迭代过程并不是同一个问题，也就是说并不是严格的最优解。若取固定信赖域，且每次迭代间均采用全步长更新寻优结果，在迭代后期可能会出现如图1的情况，各个状态变量在迭代后期产生剧烈振荡，难以符合停机准则，导致寻优失败。

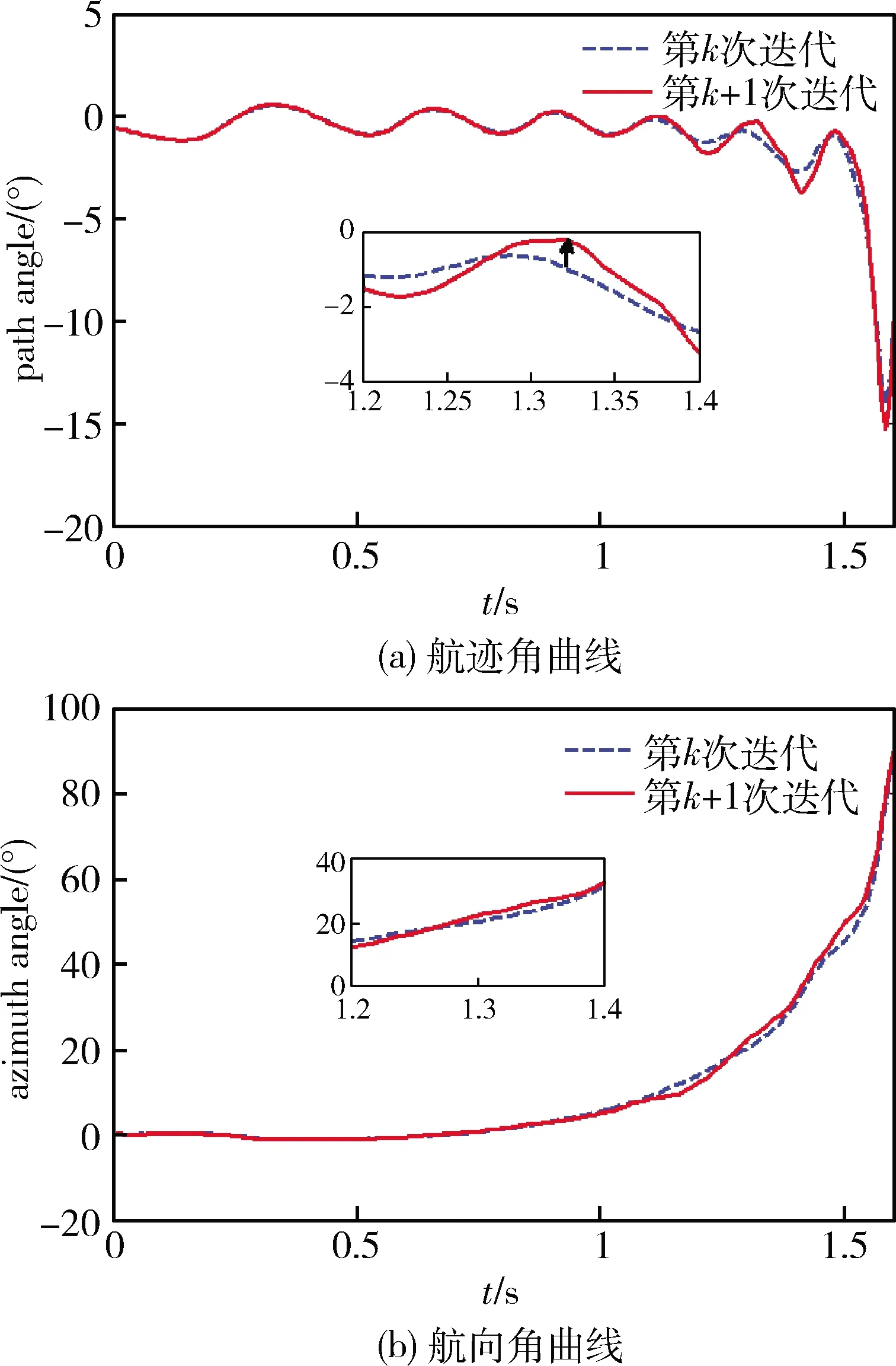
图1 振荡现象

针对这种具有两个局部极小值，得益于牛顿法的启发，本文提出一种“回溯搜索”的收敛办法。通过设置阻尼步长和回归搜索来快速处理这种局部极小值问题。具体过程如下：

(1)初值选取，并线性化，取两个回溯参数α∈(0,1],β∈(0,1]以及信赖域Δ0

(2)解决子SOCP问题，得到Δx。

(3)判断停机准则。

(4)判断回溯条件：IFJ(k+1)>J(k)，x(k+1)=x(k)+αΔx，Δ0=βΔ0，进入步骤(1)。

该回溯搜索的关键点在于信赖域的收缩权值以及阻尼步长权值的选取，调试初期可先设为黄金分割数，后期在具体的仿真过程中适当调整。综上所述，基于序列凸优化的轨迹优化流程如图2。

图2 序列凸优化的求解流程

3 仿真分析

3.1 问题描述

本节以美国某一可重复使用飞行器的再入轨迹优化为例，对第2节提出的轨迹优化方法进行仿真分析验证。其质量m=104305kg，气动参考面积S=391.22m2，气动模型如下

CL=-0.041065+0.016292α+0.0002602α2

(18)

(19)

借鉴航天飞机程序攻角的设计方法，采用典型的二次分段标称攻角剖面，其具体表达形式为

(20)

仿真中暂不考虑飞行时间对轨迹的影响，规定总再入时间tf=1600s，离散点总数为200，为保证计算的效率，设定最高迭代次数为100次。仿真所需参数见表2。仿真中，序列凸优化算法中信赖域约束和收敛条件如下

(21)

(22)

3.2 结果分析

本文的仿真均是基于Matlab环境，调用Mosek8.0[18]的求解子凸问题的求解器，以初始状态和末端状态的直线为初始参考轨迹，由于凸优化具有多项式时间复杂度，且局部最优解即全局最优解等特点，因此该寻优时间比较短，大约迭代5～7次就基本收敛，整个寻优过程耗时大约为7s，具有在线轨迹计算的潜力，具体结果如图3。

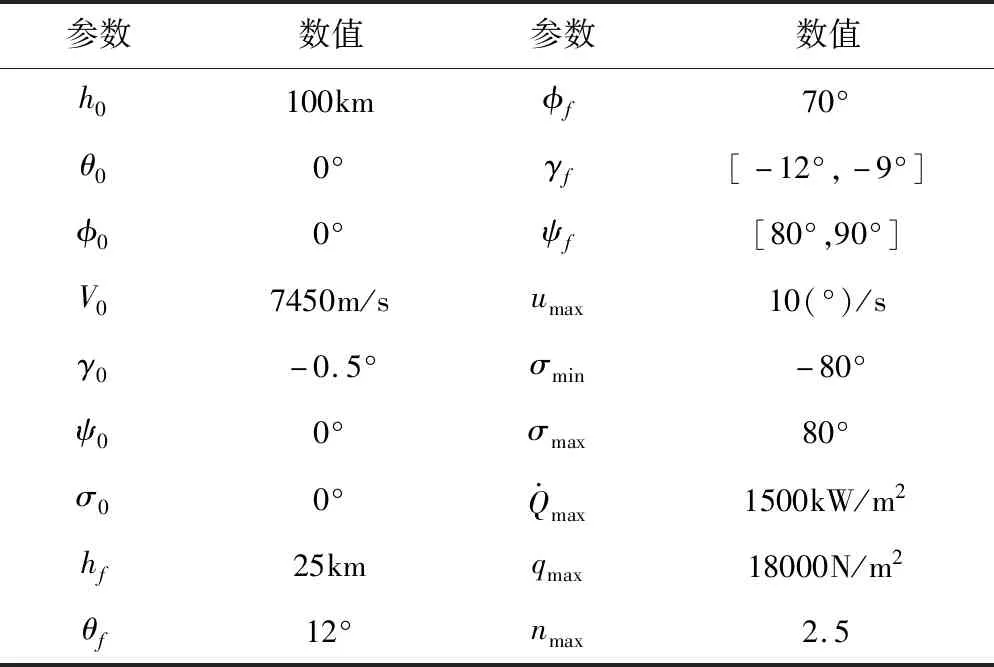
表1 再入飞行参数

图3 序列凸优化优化结果

图3(a)是优化结果中的速度-高度曲线和热流、动压、过载等路径约束的示意图，在提供再入点与终点连线的轨迹作为初始参考值的情况下，序列凸优化技术也很好地求解出满足各非线性约束的最优轨迹，表明该方法对初值的依赖度较低，鲁棒性较强。图3(c)是对控制量分别进行均匀离散和B样条曲线离散的寻优结果，可以发现，本文采取的方法有效避免了数值计算中锯齿化现象，使得寻优结果更为光滑可行。

为考察序列凸优化方法对禁飞区的规避机动能力，在问题P1的基础上加入禁飞区约束，该约束模型具体为

(23)

其中，θc和φc分别为禁飞区中心经度与纬度，RC为禁飞区半径。很显然，该约束也是非凸的，也需要进行凸化处理，这里依然采用线性化的方式进行松弛凸化。

(24)

现分别在仿真过程中设置2个禁飞区，其禁飞区半径分别为200km和400km，最终经过数次迭代，得到如下结果：

图4 考虑禁飞区的优化结果

由图4可知，本文所提的序列凸优化算法对于禁飞区有比较强的机动绕飞能力，即使在初始参考轨迹违背约束的情况下，也能通过虚拟控制量以及数次迭代的方法将其拉回安全区域，保证了飞行器能够安全、可靠地完成再入任务。

4 结论

本文针对传统轨迹优化算法效率低、对初值敏感程度高等问题，提出了一种改进的序列凸优化算法，通过b样条离散、回溯搜索等策略，提高了算法的稳定性、快速性和寻优结果的光滑性。仿真结果表明，即使是在不符合动力学约束的初末状态连线作为初值的情况下，该算法依然快速、有效地得到了满足各项约束的最优轨迹，具有一定的工程应用价值。