一种基于任务分区的轨道转移飞行器轨迹重规划方法

马昊磊 陈 攀 徐 帆 李学锋

1.北京航天自动控制研究所，北京 100854 2.宇航智能控制技术国家级重点实验室，北京 100854 3.西昌卫星发射中心，西昌 615000

0 引言

轨道转移飞行器又称为上面级火箭，是一种由运载火箭基础级发射送入近地轨道后，通过多次变轨将有效载荷送入预定工作轨道的独立飞行器。我国自主研发的“远征”系列轨道转移飞行器已完成包括北斗导航系统组网在内的多次飞行任务[1]。面对未来航天任务多元化的发展趋势，轨道转移飞行器必须具备对故障的自主处理能力。当任务过程中出现飞行偏差时，轨道转移飞行器通过轨迹重规划设计，实时评估剩余入轨与控制能力，动态处理飞行过程约束，实现在线重规划问题求解，从而最大限度地提高飞行任务的可靠性。

通常情况下，轨道转移飞行器的发动机推力大小不可调节，重规划问题主要对发动机工作时间与推力方向进行优化求解。近年来，轨迹重规划问题多选用较为复杂的三维运动模型，优化算法需要考虑多路径约束与多终端约束[2]，并设法解决实时性问题。现代计算机技术的发展，使得基于数值方法的轨迹规划问题快速求解[3]成为可能。采用凸规划的方法可以有效降低求解问题的复杂度，能够在保证精度[4]的前提下实现快速规划[5-6]。本文设计了一种任务分区方案，重构了优化问题的约束条件与性能指标，采用序列凸规划[7]完成了不同情况下的优化问题求解，重新规划出满足条件的飞行轨迹。如果飞行故障或偏差较大导致无法进入目标轨道，则通过任务降级进入次优轨道。

1 问题描述与轨道参数

轨道转移飞行器的轨迹重规划问题可以转换为非线性系统的最优控制问题，包括性能指标、状态方程、约束条件(等式约束与不等式约束)三部分。最优控制问题要求在满足状态方程和约束条件下，使得性能指标达到极小值，标准形式可以写为

(1)

其中，E[x(t),u(t),t]为等式约束条件，I[x(t),u(t),t]为不等式约束条件。

在地心惯性坐标系OE-XEYEZE中描述飞行器的质心运动方程，原点OE位于地球质心，OEXE在地球赤道平面内指向春分点，OEXEYE平面为赤道平面，OEZE为地球自转轴，指向北极。轨道转移飞行器高空飞行时可以忽略空气动力的影响，根据牛顿第二定律，在地心惯性坐标系中建立飞行器的运动状态方程

(2)

优化过程中的约束条件主要包括端点约束、控制约束以及过程约束。初始端点约束为

x(t0)=x0∈R7

(3)

其中，x0=[r0T,v0T,m0]T为飞行器轨迹重规划的初始状态。在飞行结束时需要到达某一个给定的目标状态，终端的目标轨道约束为

r(tf)=rf∈R3,v(tf)=vf∈R3

(4)

其中，rf和vf分别是目标轨道的位移矢量与速度矢量。飞行器在中心引力场轨道上无动力运行时，存在保持不变的特征轨道参数，可以由此描述目标轨道的约束条件。综合二体运动方程与矢量微分法则，可得飞行器在目标轨道上无动力运行时的动量矩[8]，即优化问题的终端动量矩约束

(5)

其中，i表示目标轨道的轨道倾角，Ω表示目标轨道的升交点赤经。

将二体运动方程与动量矩H进行叉乘运算可得

(6)

根据矢量三重叉乘法则可得

r×H=r×(r×v)=(r·v)r-
(r·r)v=rvr-r2v

(7)

将式(7)代入式(6)可得

(8)

对式(8)求积分可得

(9)

式中c为积分常矢量，由此可得飞行器在目标轨道上运行时的轨道常矢量

(10)

在圆轨道上运行时，目标轨道常矢量为0。

飞行器在目标轨道无动力运行时的能量可以表示为

(11)

其中，a表示目标轨道的半长轴(圆轨道为目标轨道半径)。当在圆轨道上运行时，其能量方程满足

r(tf)[v(tf)]2=μ

(12)

2 轨迹重规划设计

2.1 任务分区

当飞行过程中出现异常状况时，需要根据当前时刻的飞行状态对轨迹进行预判，通过任务决策规划确定下一步的行动目标。采用任务分区的方法，考虑飞行过程中轨道倾角偏差、远地点高度偏差等因素，根据偏差范围对任务决策进行分类。以判断轨道倾角与远地点高度偏差为例，在出现飞行偏差时的任务决策分区如图1所示。

图1 飞行异常状况下的任务分区

当轨道倾角与远地点高度偏差较小时，飞行器通过自适应调整或重新规划轨迹可以将载荷送入目标轨道。当超出临界范围，飞行器无法直接通过轨迹重规划将载荷送入目标轨道，此时需要分析飞行任务的可达边界范围，采用任务降级方案规划出次优轨道(救援轨道)。任务决策分类见表1。

表1 飞行异常状况下的任务决策分类

任务分区需要综合利用飞行器信息确定偏差范围，根据飞行状态确定任务决策，生成相应的制导和控制诸元。飞行器可以采取自适应调整入轨、轨迹重规划入轨、任务降级重规划等不同的任务策略。

当存在小范围飞行偏差时(I区)，飞行器不需要重规划设计，采用原有的制导和控制指令就可以将载荷送入目标轨道。

当超出总体给定的偏差，但超出偏差范围不大时(II区)，采用轨迹重规划设计，综合考虑飞行器的实时状态与任务约束条件，通过快速规划算法得到满足终端任务要求的转移轨道，将载荷送入目标轨道。重规划过程中先得到优化问题的收敛解，进而通过改进优化算法获得更高精度的优化解。

当飞行超出的偏差范围过大时，载荷不能进入目标轨道。在尚未造成致命性故障时(III区)，飞行器采用任务降级重规划策略将载荷送入次优轨道。降级轨道任务设计需要考虑飞行任务的特点和需求，分析飞行器在给定初始状态和能量约束条件下能够到达的空间集合。任务降级策略可以根据任务需求、后续调整难度、可实现性等因素，在可达范围内选择合适的性能指标与终端约束条件。任务降级轨道的选取应尽可能保证靠近原目标轨道，在轨迹规划设计中执行这一策略，令终端状态与目标点状态以等比例形式靠近。目标圆轨道选取最大半径作为性能指标可以在一定程度上保证与原目标轨道尽可能小的转移范围，以便于航天器后续的轨道机动调整。

2.2 优化问题求解

最优控制问题以有限推力作用下的质心运动模型作为状态方程，求解最优的发动机工作时间与推力矢量方向，在满足运动状态方程与约束条件下求解最优性能指标。航天器入轨任务中，由于圆轨道相位调整较为方便，目前绝大部分载荷的入轨目标轨道都是采用圆轨道[9]。以圆轨道作为目标轨道完成轨迹重规划问题描述。圆轨道上的位移矢量与速度矢量相互垂直，因此有

rT(tf)v(tf)=0

(13)

在线轨迹重规划任务II区的终端约束为满足任务需求的圆轨道，即

r(tf)=rset

(14)

其中rset为设定的满足任务需求的轨道半径大小。

采用序列凸规划完成优化问题实时在线求解，其核心思想是将原始问题转化为具有线性性能指标、等式约束、不等式约束及控制边界约束松弛的标准凸规划问题，通过不断迭代更新求解近似后的凸规划问题，以此逼近原问题的局部最优解[10]。基于序列凸规划的轨迹快速优化方法，可以将多约束下的轨迹优化问题转化为一系列有限时间内的凸规划问题，利用凸规划工具[11]进行快速寻优，得到最优飞行轨迹，保证在高精度的前提下，快速实施轨迹优化。凸规划求解需要处理模型中的非凸因素。

由于发动机推力为非凸约束，无法采用凸规划方法求解。另外，动力学方程中存在不易于凸规划求解的状态方程，因此也要进行一定的处理，将其转化为易于求解的形式。飞行器的推力加速度为

(15)

推力加速度的幅值为

(16)

采用变量代换设计，令

z(t)=ln[m(t)]

(17)

选择飞行器的位移、速度、质量变换量作为状态变量x=[rx,ry,rz,vx,vy,vz,z]T，推力加速度的分量与幅值作为控制变量u=[aTx,aTy,aTz,w]T，运动状态方程(2)可以转换为

(18)

在轨迹重规划问题中，通常发动机的推力大小不可调节。推力加速度的幅值约束可以表示为

(19)

对Tconste-z(t)关于z0(t)进行Taylor展开并保留线性项可得

0≤w(t)≤Tconste-z(t)[1-z(t)+z0(t)]

(20)

式(20)满足二阶锥约束，可以使用凸规划方法快速求解。由于飞行器的终端质量具有下限mlow，因此有

z(tf)≥ln(mlow)

(21)

为了提高序列凸规划求解的迭代速度与收敛性，在控制变量约束中引入迭代过程变量VI。结合罚函数法的优化思想，在性能指标函数中加入迭代过程变量的惩罚系数，从而保证迭代求解结束时的过程变量为0。在轨迹自主规划设计中执行这一策略，在飞行异常状态处于任务II区时，选取燃料消耗最少(即终端状态质量最大)作为重规划入轨的性能指标函数。根据最优控制理论对这一问题进行求解，构造最优控制问题。

(22)

其中状态方程可由式(18)确定，等式约束由中心引力场特征轨道参数及目标圆轨道几何特性确定。

在飞行异常状态处于任务III区时，构造任务降级轨道，选取终端状态轨道半径最大作为重规划入轨的性能指标函数。即移除式(22)中的目标轨道半径rset约束，并将式(22)中的性能指标函数调整为

minJ=-r(tf)+ηVI(tf)

(23)

根据上述最优控制问题描述，对性能指标、状态方程与约束条件进行离散化、归一化处理，选用初始状态量作为序列凸规划的迭代初值，采用原始-对偶内点法[12]完成轨迹重规划问题求解。

3 仿真分析

以轨道转移飞行器入轨任务为例，当飞行过程中出现异常偏差时，采用轨迹重规划方案确定任务目标轨道的约束条件，并采取相应的执行策略。当飞行偏差较小，处于任务I区时，轨道转移飞行器可以通过自适应调整实现入轨，调整后的飞行控制诸元保持不变，此时无需重新规划飞行轨迹。因此主要考虑飞行偏差处于II区和III区情况下的重规划方案。

3.1 仿真案例1

轨道转移飞行器的发动机参数为：总质量10600kg，燃料质量5600kg，真空推力13000N。

选取轨道转移飞行器第1次点火作为问题的初始状态点。当t=0s时，飞行器由于故障导致推力出现偏差，无法按照原定计划完成任务。假设推力偏差情况下发动机仍能正常关机与二次点火，且发动机比冲保持不变，剩余燃料能够充分燃烧。依据飞行器的入轨能力评估，重新规划任务轨迹(任务II区)，结合当前的剩余燃料和目标轨道根数要求，考虑飞行约束情况，通过轨迹重规划实现飞行任务，如图2所示。

图2 轨迹重规划入轨-任务II区

轨道转移飞行器的重规划转移轨道与原任务转移轨道半长轴、推力加速度、飞行速度对比如图3～5所示，其中虚线为原转移轨道的变化情况，实线为重规划转移轨道的变化情况。

图3 任务II区重规划-半长轴对比

图4 任务II区重规划-推力加速度对比

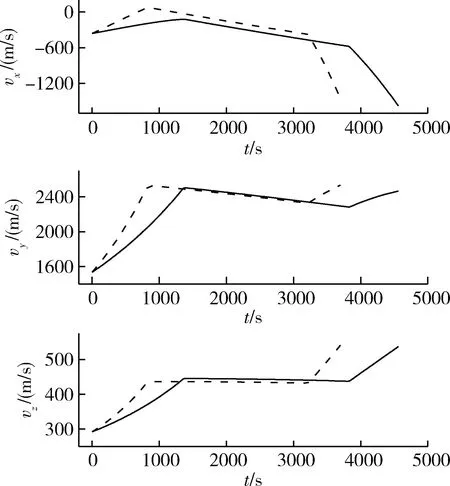
图5 任务II区重规划-飞行速度对比

仿真案例1采用轨迹重规划设计，轨道转移飞行器能够在到达原定的任务目标轨道，终端轨道参数为：半长轴44971.0km，偏心率0，轨道倾角10.6°，升交点赤经21.2°。

3.2 仿真案例2

选取与仿真案例1相同的飞行器参数。当二次点火飞行偏差较大时，飞行器无法到达目标轨道。若第2次点火时，飞行器的远地点高度偏差为500km，轨道倾角偏差为1°，考虑飞行约束情况，采取任务降级入轨模式(任务III区)。通过轨迹重规划实现降级入轨，如图6所示。

图6 轨迹重规划任务降级-任务III区

轨道转移飞行器的降级规划转移轨道与原任务转移轨道半长轴、轨道倾角、推力加速度、飞行速度对比如图7～10所示，其中虚线为原转移轨道的变化情况，实线为重规划转移轨道的变化情况。

图7 任务III区重规划-半长轴对比

图8 任务III区重规划-轨道倾角对比

图9 任务III区重规划-推力加速度对比

图10 任务III区重规划-飞行速度对比

仿真案例2对原定目标轨道进行了任务降级，并重新规划了入轨飞行轨迹。轨道转移飞行器能够到达与原目标轨道共面的次优轨道，终端轨道参数为：半长轴44563.4km，偏心率0，轨道倾角10.6°，升交点赤经21.2°。

4 结论

针对轨道转移飞行器的异常偏差问题，提出了一种基于任务分区的轨迹重规划方法。将轨迹重规划问题转化为最优控制问题。根据轨道倾角与远地点高度偏差，确定不同情况下的任务策略与目标轨道参数，构造相应的性能指标与约束条件。采用序列凸规划实现入轨轨迹的快速重构，实现了不同偏差状况时的轨迹重规划设计。以航天发射中常用的圆形目标轨道任务为例，当偏差较小时，采用自适应调整或轨迹重规划设计可以保证飞行器顺利进入原目标轨道；当偏差较大时，采用任务降级重规划设计，尽可能保证飞行器进入与原目标轨道共面的次优轨道。仿真结果表明本文提出的方法能够适应不同的飞行异常状况，快速规划出满足任务要求的入轨轨迹，实现可达任务剖面的最大化。