多约束下小卫星的能量最优主动碰撞规避控制*

王国刚 戴 路 徐 开 刘克平 李 峰，范林东

1.长光卫星技术有限公司，长春130000 2.长春工业大学，长春130000

0 引言

由于商业小卫星公司迅速崛起，商业卫星迅速发展。快速增多的低轨卫星数量，增大了卫星间的碰撞风险系数。碰撞规避是防止低轨小卫星碰撞的有效手段和方法[1-4]。由于测控站的数量有限，如果几颗卫星同时存在碰撞可能，那么仅通过地面同时对多颗卫星规避控制的压力是极大的。

目前，卫星间的碰撞是必须考虑的重要问题[5-6]，文献[7]针对航天器与空间目标距离较近的碰撞问题进行了研究，依靠星上测量设备，设计了近距离自主规避策略，但是未考虑测量设备的测量误差。近距离规避碰撞，仍会存在碰撞的风险。文献[8]根据卫星编队的特点及碰撞规避的需要, 使用协同进化粒子群优化算法对重构问题采用既独立又集中的求解方式,完成了编队重构，但是计算时间相对较慢。文献[9]提出一种基于特征点的快速解析碰撞预警方法，降低了对绝对测量信息的依赖，通过割线法和高斯方程求解燃料最省的碰撞规避，但是求的解均是近似解，会存在一定偏差。文献[10]将碰撞概率密度函数在危险区域积分，获得编队卫星的碰撞概率，当碰撞概率大于安全阈值时，向卫星施加最小脉冲速度修正量，降低了碰撞概率，但是碰撞规避机动后未保持星座构型。文献[11] 根据撤离后飞船、天宫以及伴星的相对运动关系研究了结合规避控制的飞船双脉冲维持优化控制方案。文献[12]提出了一种求解交会对接过程中最优碰撞规避机动方法，在保证碰撞概率降低到安全值的前提下，得到最优的碰撞机动冲量，采用机动方向和机动大小分布求解的策略计算冲量，适用于相距几十公里以内的碰撞规避，而不适用于近距离的碰撞规避。文献[13]针对航天器燃料最优编队初始化、重构等机动展开研究，提出了一种燃料最优的解析控制方法，该方法形式简单，计算量小，但燃料消耗量最优解取决于初始状态误差。

本文考虑了星座构形约束、测控资源约束和载荷约束，设计了卫星间近距离碰撞的规避控制策略，该策略不完全依靠测量设备，且不需要初始状态误差，采用最优控制理论，实现能量最优化碰撞规避控制。

1 问题描述

1.1 控制策略

两颗卫星d和g正常在轨飞行，当t时刻，卫星d与卫星g相交于空间某一点时两颗卫星发生碰撞，卫星d相对于卫星g的位置矢量为

ρ=r1-r2

(1)

式中：r1为卫星d的地心矢径，单位为km，r2为卫星g的地心矢径，单位为km，见图1。

图1 卫星间碰撞示意图

当航天器的相对位置矢量ρ的模ρ小于目标轨道半径时，满足航天器相对运动方程[14]，表示为：

(2)

1.2 坐标变换

以上的运动方程及初始状态和目标状态条件均是在卫星质心坐标系下给出的，因此需要将卫星质心坐标系转换到轨道坐标系，再转到地球惯性坐标系进行控制。

从图1可看出，卫星g在质心坐标系下绕Yd轴转-φ，再绕Zd轴转ζ，则卫星质心坐标系到轨道坐标系的转换矩阵TD为：

(3)

式中：RZ(ζ)表示绕Zd轴的旋转矩阵，RY(-φ)表示绕Yd轴的旋转矩阵。

轨道坐标系转到地球惯性坐标系的转换矩阵TT为：

(4)

1.3 约束建模

1.3.1 载荷约束

遥感小卫星的载荷与高度密切相关，当轨道高度越高，载荷的分辨率将会下降，不满足用户需求；当轨道高度越低，卫星的轨道衰减越快，使用寿命大大减少。

假设成像载荷设计的分辨率为fl，分辨率允许偏差值为fp，可运行在轨道高度为H，则卫星轨道允许的高度为

(5)

轨道高度偏差就是载荷对轨道高度的约束，轨道半长轴满足

H+ae≤Hp+ae

(6)

式中：ae为地球半径，ae=6378.137km。

1.3.2 测控资源约束

首先确定可利用的测控站，尽量选择在测控弧段内进行轨道规避调整，当可以预测到碰撞位置和时刻后，选择可利用的测控站进行控制指令发送，执行规避控制。

(7)

碰撞时刻为t，则控制约束为

t-T>TL

(8)

式中：TL为规避控制提前时间，TL>6h，当最接近TL的测控站资源被占用，调用次接近TL的测控站资源，依次递推，得出适合的测控站资源，当判断出卫星间要发生碰撞时，提前T的时间进行碰撞规避控制。

1.3.3 星座构形约束

对于商业遥感星座，重访和覆盖是客户最为关心的能力，相位分布情况直接影响重访能力，因此，相位分布的保持尤为重要，若同一个轨道面上的卫星高度相差较大，几天时间就会超出允许相位差，因此控后尽量回到原来的高度或百米级的高度差。

假设速度增量为u，卫星角速度为n，则半长轴变化量Δa为

(9)

卫星轨道周期为T，轨道控制后周期为Th，则每天的相位漂移速度为

(10)

(11)

2 碰撞规避控制设计

2.1 控制策略

对于碰撞规避，通过改变相对半长轴控制量来实现星间的安全飞行。假设两颗卫星，一颗为在轨正常运行的目标卫星，另一颗规避卫星不断靠近目标卫星，采用主动控制策略，假设规避卫星从A点到B点的轨迹路径上的任意一点到目标卫星的距离为r(t)，目标卫星的安全球半径为rs，则定义规避卫星在轨迹路径上与安全球的距离为

Δr(t)=r(t)-rs

(12)

式中：为规避卫星在轨迹路径上与安全球的距离，单位为m；将安全球半径为rs的最小值Δr(t)min作为判断是否发生碰撞的准则，判断准则如下：

(13)

式中：rs=rs1+rΔ，rΔ为预留距离，单位为m；rs1表示规定的安全距离，单位为m。

当Δr(t)min>0时，规避卫星与目标卫星不会发生碰撞；当Δr(t)min=0时，规避卫星与目标卫星存在碰撞的风险；当Δr(t)min<0时，规避卫星与目标卫星会发生碰撞。

2.2 最优规避控制设计

(14)

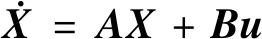
(15)

式中：A为系数矩阵，B为常数矩阵，表达式为

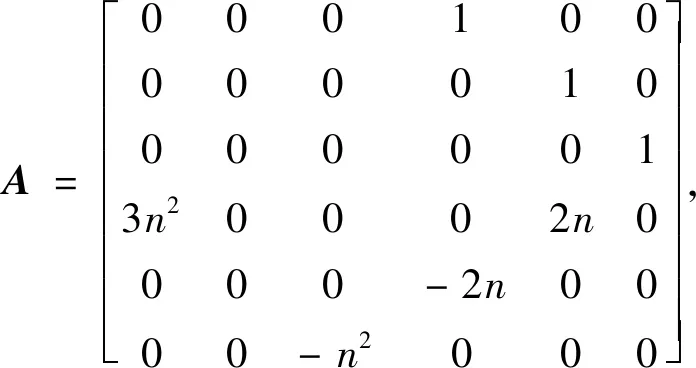
控制终端状态为

X(tf)=Xtf

(16)

式中：X(tf)表示tf时状态，Xtf表示状态值，tf表示时间，给定时间tf，选取能量优化指标J为

(17)

根据极小值原理，选取哈密顿函数H为：

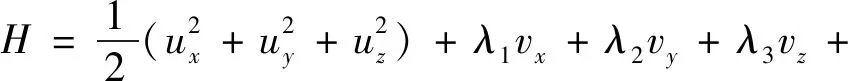
(18)

式中：λ1，λ2，λ3，λ4，λ5和λ6均为协调因子，vx，vy和vz分别表示Xd轴，Yd轴和Zd轴的相对速度，n为目标轨道平均角速度，[ux,uy,uz]T为速度增量，单位为m/s，则协态方程为：

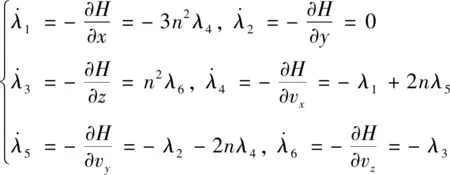
(19)

可求解得

(20)

式中：μi(i=1,2,…,6)表示待定常数，t表示时间，nt表示t时间内转动的角度。

根据极小值原理，最优控制应使哈密顿函数H达到极小，即

(21)

将式(20)～(21)带入式(2)中，可得

(22)

规避卫星的初始条件和终端条件如下

(23)

式中：X(0)表示0时刻的状态，X(tf)表示tf时状态，x0，y0和z0分别表示Xd轴、Yd轴和Zd轴的初始位置，vx0，vy0和vz0分别表示Xd轴、Yd轴和Zd轴的初始速度，xtf，ytf和ztf分别表示Xd轴、Yd轴和Zd轴的终端位置，vxtf，vytf和vztf分别表示Xd轴、Yd轴和Zd轴的终端速度。

由于Zd轴的运动是独立的，因此将式(23)带入式(22)中，可得

(24)

式中：S为sin(nt)缩写，C表示cos(nt)缩写，tf表示终端时间。

由于Xd轴和Yd轴存在耦合，通过解微分方程，利用初始条件和终端条件求得一次代数方程组为：

(25)

S=sin(ntf)，C=cos(ntf)。

通过式(25)可求得μ1，μ2，μ3和μ4，则卫星最优速度增量为

(26)

通过卫星最优速度增量和方向，卫星以最优条件下的运动轨迹进行碰撞规避。

3 算例分析

3.1 仿真输入

1)选择二体递推模型进行递推；

2)轨道初始值和控制策略参数见表1和表2；

表1 卫星初始轨道参数

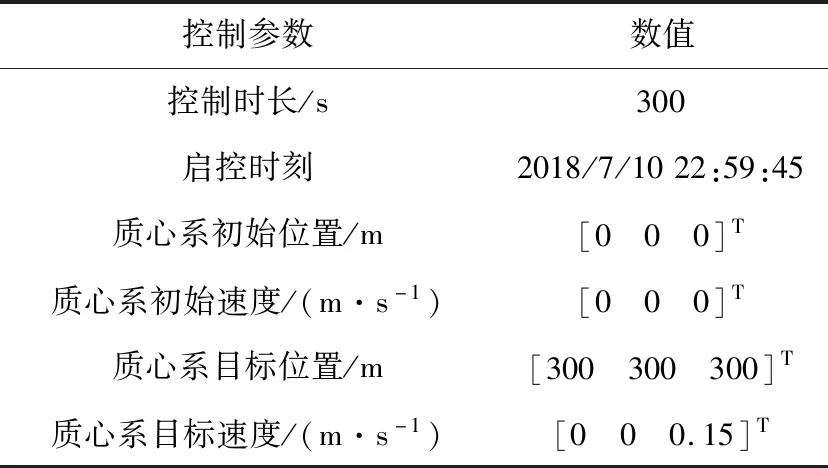
表2 控制策略参数

3)最小安全距离设置为300m，小于300m时即发出预警，并进行碰撞规避。

根据有效载荷，星座构形约束、测控资源约束等数学模型，可知:

当有效载荷分辨率为1m，其轨道高度为500km，允许分辨率上限为1.002m，则允许调整的轨道高度不高于501km；

当规避星轨道有2颗卫星，以180°等相位分布，允许相位偏置7°，当调整50m时，相位差飘出0.059(°)/d，则118d飘出应用需求允许范围，因此允许调整的轨道高度范围为±50m以内；

可用的测控站为长春站、三亚站和喀什站，启控时刻尽量选择在可利用的较近的测控弧段内。

3.2 数值仿真

采用Matlab进行数值仿真，仿真时间12h，设置目标星安全距离为300m，两颗卫星2019.2.20 03:59:45开始发生碰撞，采用2种控制方法进行碰撞规避，通过常规PD控制策略与最优控制策略的消耗和能量进行对比，证明最优控制策略的优势，燃料最优规避控制策略仿真和常规PD控制规避控制策略仿真见图2～3。

将质心系下的位置和速度通过坐标转换到惯性系下，惯性系下的卫星轨道见图5。

当两颗卫星距离小于300m时，卫星将要碰撞，提前6小时在测控弧段内开始进行轨道碰撞控制，从图6～7可知，轨道半长轴控制量最大不超过28.3m，满足星座构形约束和有效载荷约束，两颗卫星碰撞规避见图8。

图2 燃料最优控制

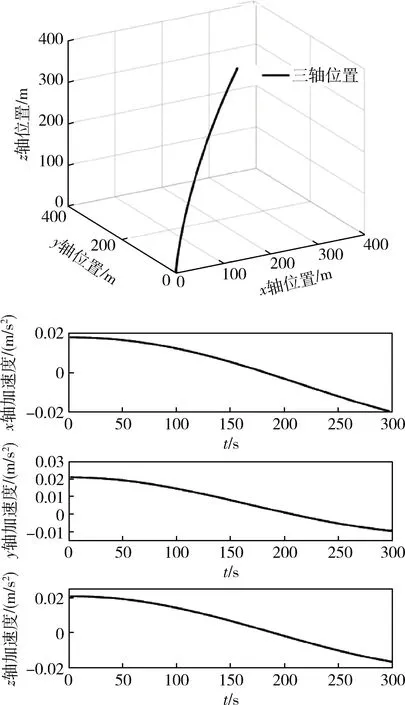
图3 常规PD控制

图4 常规PD控制和最优控制和能量

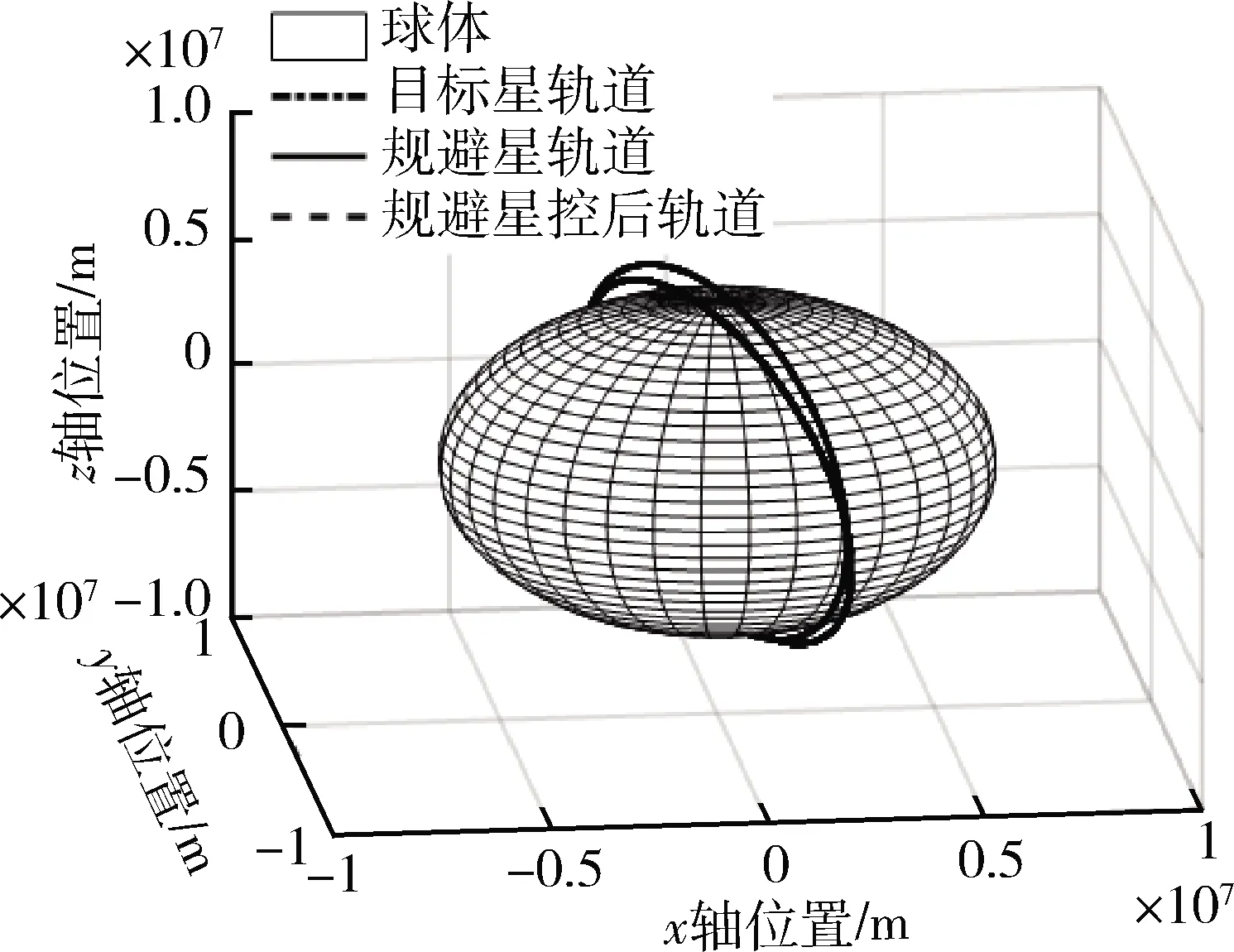
图5 惯性系下卫星轨道

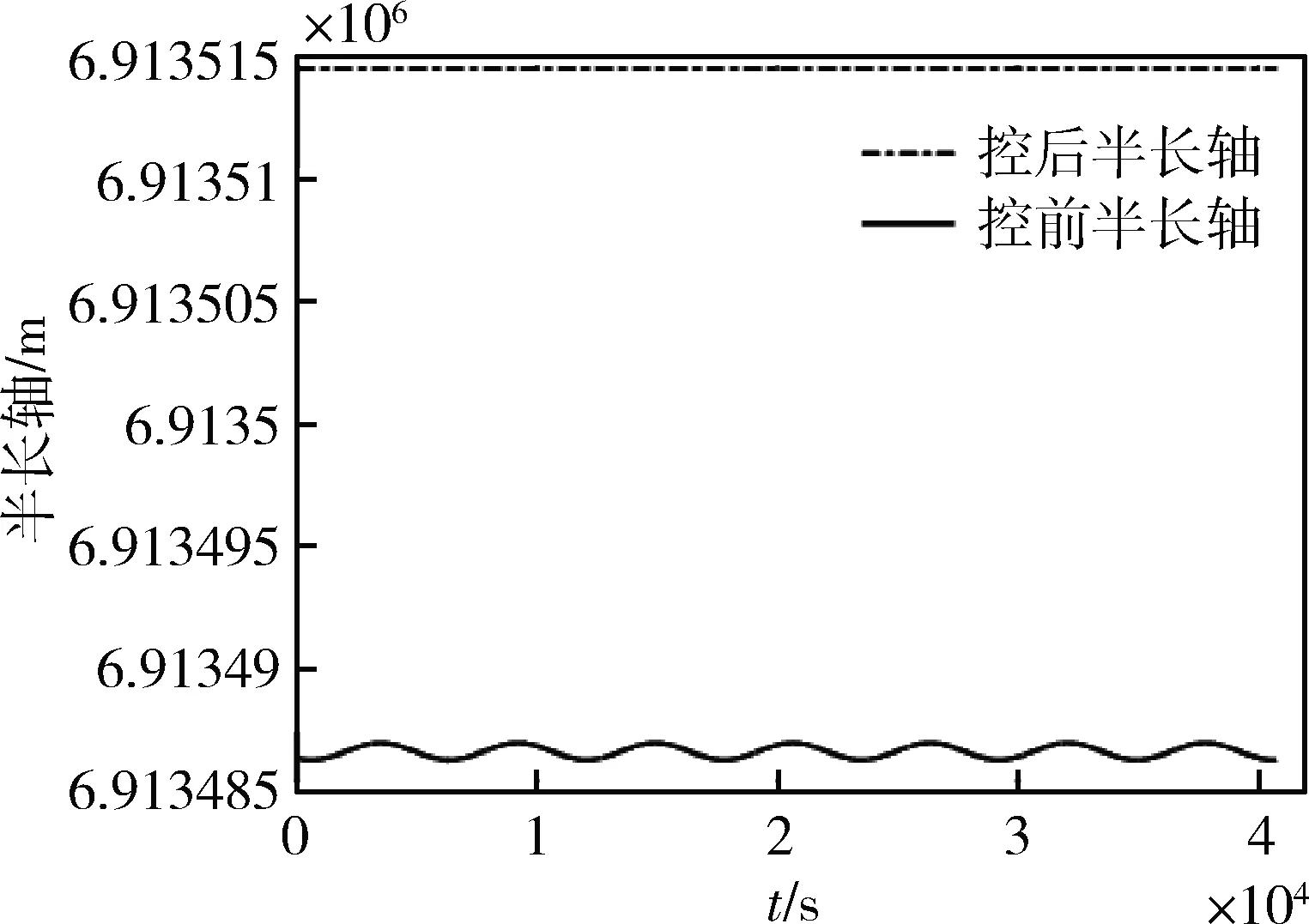
图6 规避星控前控后轨道半长轴

图7 轨道半长轴控制量

图8 碰撞规避图

从图8可知，当2018.7.11 03:59:45时，两颗卫星的距离小于300m，碰撞规避控制后的两颗卫星最小距离为8000m，以最优燃料控制规避了两星碰撞。

仿真效果可知，满足各类约束的情况下，采用设计的自主碰撞规避算法很好地实现了卫星的自主碰撞规避，证明了最优碰撞规避算法的有效可行。

4 结论

设计了一种多约束下的能量最优的主动碰撞规避控制，建立了小卫星的运动学模型和约束模型，在此基础上制定了碰撞规避策略，通过小卫星能量最优化指标和哈密顿函数，给出最优条件下的速度增量和方向，实现了卫星间碰撞规避。