服务航天器主动绕飞观测的建模与控制

王首喆 张庆展

上海宇航系统工程研究所，上海 201109

0 引言

服务航天器执行在轨维修、燃料加注、碎片清除等任务时，为获取目标准确信息，需对目标进行近距离全方位的绕飞观测。通常服务航天器相对目标质心进行绕飞；对于体积庞大、构型复杂的航天器(如国际空间站)，存在相对目标局部区域绕飞观测的需求。当服务航天器的初始位置与绕飞轨迹相距较远时，如何安全平稳地进入绕飞轨迹，如何对绕飞轨迹与观测姿态进行协同规划，是本文研究的重点。

航天器间相对运动常以C-W方程[1]为基础进行研究。文献[2]对多脉冲控制下共面快速绕飞的进入段、绕飞段和撤离段进行了设计。文献[3]以C-W方程和脉冲控制为基础，给出了自然轨迹、受限轨迹的数学描述，对全局绕飞轨迹、局部限制轨迹进行了多种模式的设计。文献[4]对恒定推力作用下绕飞的形成与保持进行了研究，将绕飞过程分为进入绕飞面和在绕飞面内形成并保持绕飞轨迹2个阶段。文献[5]的目标为椭圆轨道，将相对动力学描述为周期性参数R、角速度、角加速度的线性时变系统，在足够小的时间区间内，进一步将时变系统用参数冻结的线性系统代替。文献[6]采用相对轨道根数描述绕飞轨迹的几何特性。编队飞行是描述绕飞轨迹的另一种有效途径。文献[7]对连续推力作用下快速圆绕飞的空间编队进行了设计。文献[8]对近地轨道卫星编队飞行提出了形式简单的用于同步控制的相对轨道动力学模型。文献[9]基于T-H方程解析解，提出一种适用于飞行器绕飞操作的GNC算法。文献[10]对航天器的相对运动，设计了相对轨道和相对姿态的鲁棒自适应控制律并给出了稳定性证明。

上述研究中，多采用相对轨道根数设计绕飞轨迹，多样性和灵活性不足。动力学建模中，仅考虑了挠性附件振动对姿态的影响，没有考虑挠性附件振动与轨道间的耦合作用。文章考虑在轨服务操作任务对相对运动构型需求的灵活性，提出了一种新颖的建模方法，将绕飞分为过渡过程和绕飞过程2个阶段。通过对方位角进行S型速度规划，使服务飞行器从任意初始方位平稳地进入绕飞平面。通过定义轨迹规划坐标系，将绕飞轨迹从三维空间转化到二维平面，实现了轨迹的降维设计。定义期望绕飞矢量，实现绕飞构型的灵活配置。定义期望姿态坐标系，解算出服务航天器绕飞观测所需的姿态。基于二体动力学模型，定义期望绕飞矢量与绕飞误差矢量，建立了相对轨道误差动力学模型，将轨道跟踪控制问题转化为调节器设计。设计了基于模态观测器的姿轨联合滑模控制律。最后对所建模型和控制律进行了仿真验证并给出结论。

1 任意方位绕飞设计

1.1 坐标系定义

文章涉及的坐标系有： 1)地心惯性坐标系Oi-XiYiZi； 2)质心轨道坐标系Oo-XoYoZo； 3)相对轨道坐标系OT-XTYTZT； 4)轨迹规划坐标系Or-XrYrZr； 5)服务航天器本体坐标系Ob-XbYbZb； 6)姿态参考坐标系Od-XdYdZd； 7)期望姿态坐标系Oq-XqYqZq。下面给出Or-XrYrZr、Od-XdYdZd和Oq-XqYqZq的定义，其余坐标系参照常用坐标系的定义。

轨迹规划坐标系Or-XrYrZr：原点Or位于目标质心，Zr轴指向绕飞平面正法线方向。Zr轴与相对轨道坐标系OT-XTYTZT的ZT轴夹角为α，Zr轴在XTYT面投影与YT轴夹角为β，这两个角称为绕飞方位角。OT-XTYTZT通过2次主轴旋转得到Or-XrYrZr，如图1所示，坐标转换矩阵为RrT=Rx(-α)Rz(-β)。此坐标系用于规划服务航天器的绕飞轨迹。

图1 轨迹规划坐标系

姿态参考坐标系Od-XdYdZd：如图2所示，原点Od位于服务航天器质心，Xd从服务航天器质心指向绕飞中心，Zd在绕飞平面且与绕飞方向反向，Yd与Xd、Zd构成右手系。此坐标系用于辅助解算服务航天器绕飞时的期望姿态。

期望姿态坐标系Oq-XqYqZq：如图2所示，原点Oq位于服务航天器质心，Xq从服务航天器质心指向目标，Zq在绕飞平面且与绕飞方向反向，Yq与Xq、Zq构成右手系。此坐标系用于服务航天器绕飞时姿态的跟踪。

图2 期望姿态坐标系

1.2 绕飞轨迹设计

初始时刻服务航天器不在绕飞面内，对目标的任意方位主动绕飞观测由过渡过程和绕飞过程2个阶段组成。

首先对过渡过程进行设计。如图1所示，rst0为初始时刻服务航天器相对目标的位置矢量，rstg为服务航天器到达绕飞面时相对目标的位置矢量，令rstg与rst0、Zr共面，且过渡过程中长度不变，rh为绕飞半径，则rstg与Zr的夹角τ计算公式为：

(1)

在rst0与期望绕飞轴Zr构成的扇形平面(小于180 °)内，将rst0向Zr旋转角度τ得到初始绕飞轴Zr0。特别地，当服务航天器初始位置rst0与Zr夹角为0°或180°时，任选OT-XTYTZT中的一个坐标轴，将rst0向该轴方向旋转角度τ得到Zr0。Zr0可由rst0和Zr表示为

Zr0=a·rst0+b·Zr

(2)

同时，Zr0满足以下公式：

(3)

(4)

根据式(1)～式(4)可得到Zr0的具体表达。

在确定初始绕飞轴Zr0后，设计由rst0到rstg的过渡过程rst(t)，即Zr0到Zr的过渡过程Z(t)。

α0和β0为Zr0的方位角，αend和βend为Zr的方位角。由于S型速度曲线能对加速度的变化率进行控制，且加速度曲线连续，在速度衔接处可实现平稳过渡，是一种能限制振动的速度控制方法[11]，所以选用S型速度曲线对方位角α(t)和β(t)进行设计。过渡过程中，根据服务航天器推力器配置情况，对加速度进行限幅。假设过渡时间为tg，在确定角加加速度、最大角加速度以及最大角速度后，并赋值α(t0)=α0，β(t0)=β0，α(tg)=αend，β(tg)=βend，即可得到方位角α(t)和β(t)的S型速度规划结果。

在Or-XrYrZr的定义中，将Zr轴用Z(t)代替，使Or-XrYrZr在过渡过程中随Z(t)同步变化，直到Z(t)与Zr重合。服务航天器在Or-XrYrZr中的位置保持不变，则rst(t)在OT-XTYTZT下可表示为：

rst(t)|T=[Rx(-α(t))Rz(-β(t))]Trst0|r

(5)

式中：rst0|r=Rx(-α0)Rz(-β0)rst0|T。

定义期望绕飞矢量l，rst(t)可视为期望绕飞矢量在过渡阶段的表示。

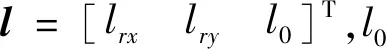
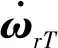
(6)

(7)

l在OT-XTYTZT系的表示为

lT=(RrT)Tlr

(8)

(9)

(10)

1.3 期望姿态解算

假设服务航天器的敏感轴为体坐标系的Xb轴，通过Oq-XqYqZq对绕飞姿态进行解算。

如图2所示，Od-XdYdZd系的作用是建立了一个虚拟的姿态参考坐标系，随着绕飞轨迹的变化，该姿态坐标系相对Or-XrYrZr只需绕Yd轴做相应旋转，便能够使Xd轴对绕飞中心O′保持定向。根据坐标系Oq-XqYqZq的定义，将Od-XdYdZd绕Zd轴旋转角度γ=90°-τ直到与Oq-XqYqZq重合，服务航天器只要对坐标系Oq-XqYqZq的姿态进行跟踪，便可以实现对目标航天器的视线指向。

(11)

(12)

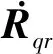
Rqr=Rz(γ)Rx(-90°)Rz(180°+θr)

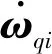
ωqi=ωqr+RqrωrT+RqrRrTωTi

(13)

(14)

式中：ωTi为OT-XTYTZT相对Oi-XiYiZi的角速度，用θt表示目标的真近点角，则ωTi在OT-XTYTZT下的表示为

(15)

2 相对动力学模型

在相对轨道坐标系OT-XTYTZT中建立包含期望绕飞矢量l的相对轨道动力学模型。

图3中，rs和rt分别是服务航天器和目标在惯性系的位置矢量，服务航天器相对目标的位置矢量为rst=rs-rt。定义实际相对位置矢量rst与期望绕飞矢量l的绕飞误差矢量为Δr，有rst=l+Δr，在OT-XTYTZT下，建立相对轨道误差运动学和动力学模型为

(16)

(17)

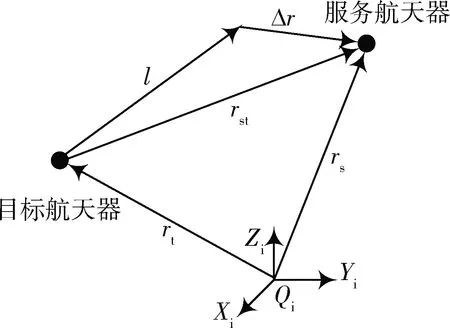
图3 相对位置关系示意图

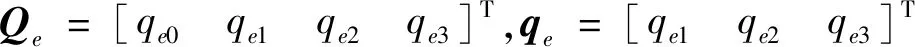
(18)

3 控制律设计

(19)

设计的滑模观测器为：

(20)

稳定性证明：

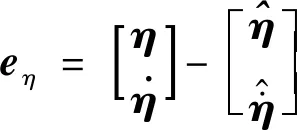
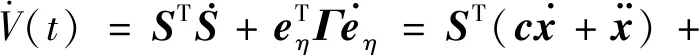
(21)

将式(18)～(20)代入式(21)得到

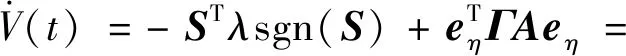
由Lyapunov稳定性定理可知，系统是全局渐近稳定的。

为了减小滑模控制的抖振，将符号函数用饱和函数sat(Si,ε)代替，表达式为

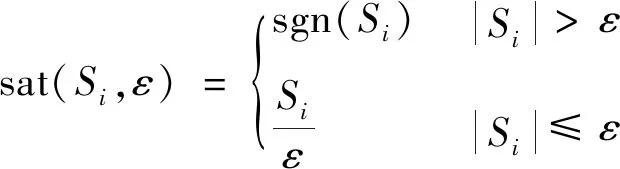
式中：ε>0，为滑模边界层的厚度。

4 仿真校验

4.1 仿真条件

目标航天器初始轨道参数：a=6778137m，e=0，i=42.8°，Ω=0°，ω=0(°)/s，f=0°。

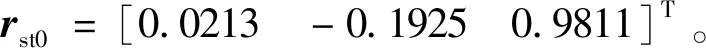
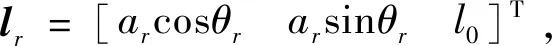
通过计算可得，Or-XrYrZr相对OT-XTYTZT的初始绕飞方位角α0=11.1690°，β0=173.6975°，期望绕飞方位角αend=80.0384°，βend=69.1196°。设计S型速度规划导引律α角和β角的加加速度均为0.01 (°)/s3，最大角加速度均为0.1(°)/s2，最大角速度均为0.5 (°)/s。

面内绕飞角θr设计为

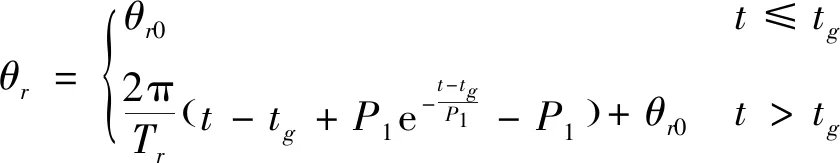
式中：Tr=800s为绕飞周期，P1=1000s为延迟系数，θr0为初始绕飞角，由绕飞段初始相对位置矢量rst0确定。

控制律参数选择：

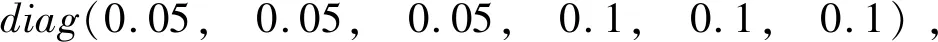
4.2 仿真结果及分析

按照上述仿真条件，对文章提出的任意方位绕飞设计方法、建立的刚柔耦合相对姿轨动力学模型和设计的基于挠性模态观测器的输出反馈滑模控制律进行仿真分析。

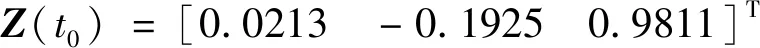
图4 服务航天器相对目标的绕飞轨迹

图8和图9分别为在OT-XTYTZT坐标系下服务航天器对期望绕飞轨迹的位置跟踪误差曲线和速度跟踪误差曲线。由图可知，在前200s的过渡阶段，服务航天器的位置跟踪误差最大为0.05m，速度跟踪误差最大为0.023m/s，在200s后，服务航天器进入绕飞阶段，跟踪误差快速收敛，位置跟踪误差为0.015m，速度跟踪误差为0.002m/s。仿真结果表明，采用设计的控制律按照文章提出的任意方位绕飞设计方法执行绕飞任务，轨控精度高，可满足服务航天器对目标绕飞的要求。

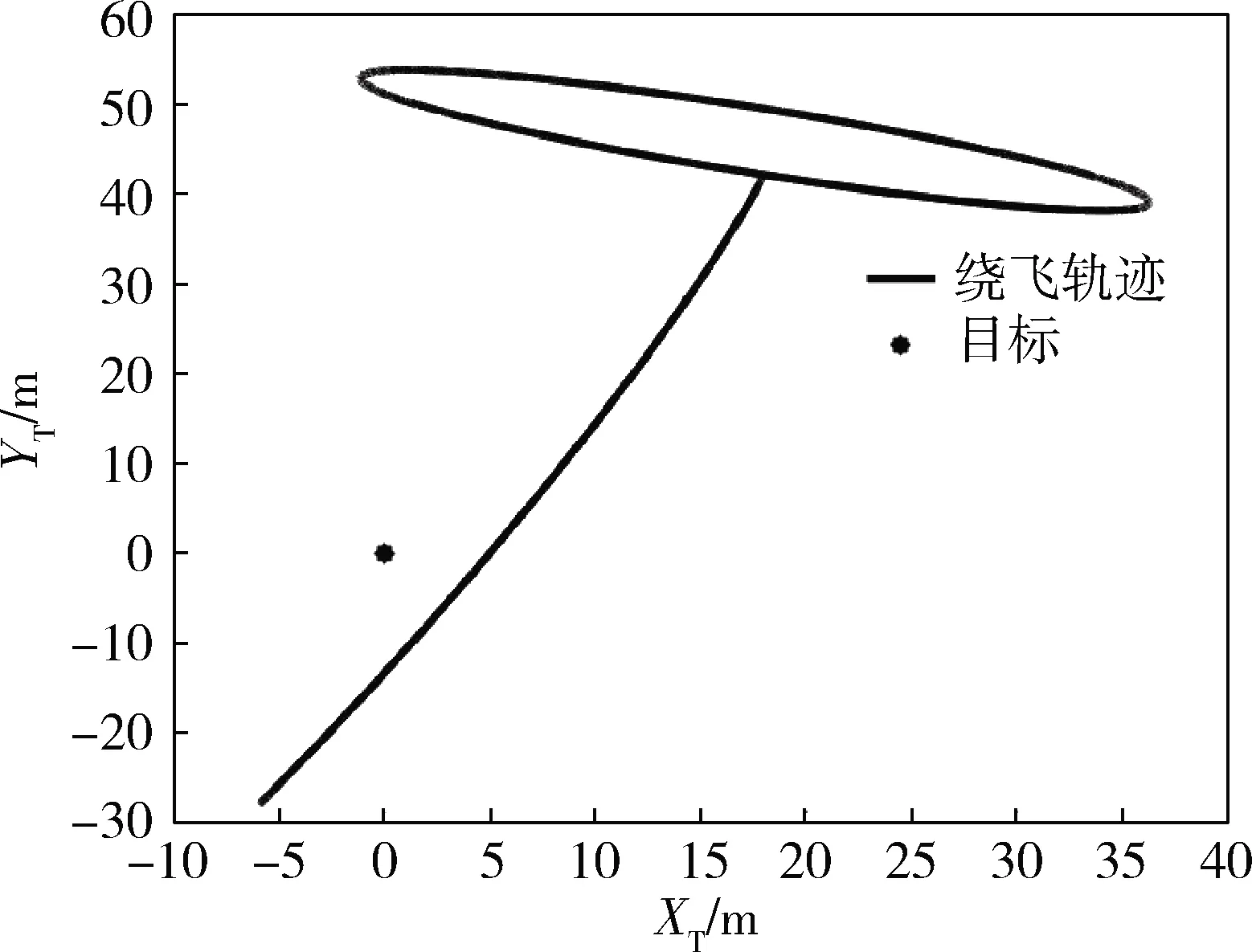
图5 绕飞轨迹在XTYT平面的投影

图6 绕飞轨迹在XTZT平面的投影

图7 绕飞轨迹在YTZT平面的投影

图8 位置跟踪误差曲线

图9 速度跟踪误差曲线

图10和图11分别是服务航天器本体坐标系Ob-XbYbZb相对期望姿态坐标系Oq-XqYqZq的姿态角跟踪误差曲线和姿态角速度跟踪误差曲线。由图可知，三轴姿态角跟踪误差最大为0.060 °，三轴姿态角速度跟踪误差最大为0.046 (°)/s。仿真结果表明，设计的控制律姿控精度高，能够使服务航天器的敏感轴跟踪期望视线轴，满足服务航天器对目标视线指向观测的要求。

图10 姿态角跟踪误差曲线

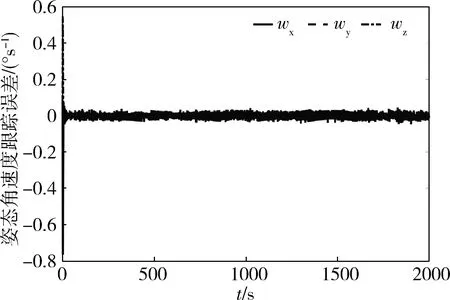
图11 姿态角速度跟踪误差曲线

图12给出了服务航天器挠性附件在绕飞过程中前3阶模态的振动曲线，模态振动快速收敛。图13为文章设计的模态观测器对挠性附件模态的观测误差曲线，第1阶模态位移的观测误差为0.026，第2阶模态位移的观测误差为0.0002，第3阶模态位移的观测误差为0.005。仿真结果表明，文章设计的模态观测器是有效的，控制律能够有效抑制服务航天器挠性附件的振动。

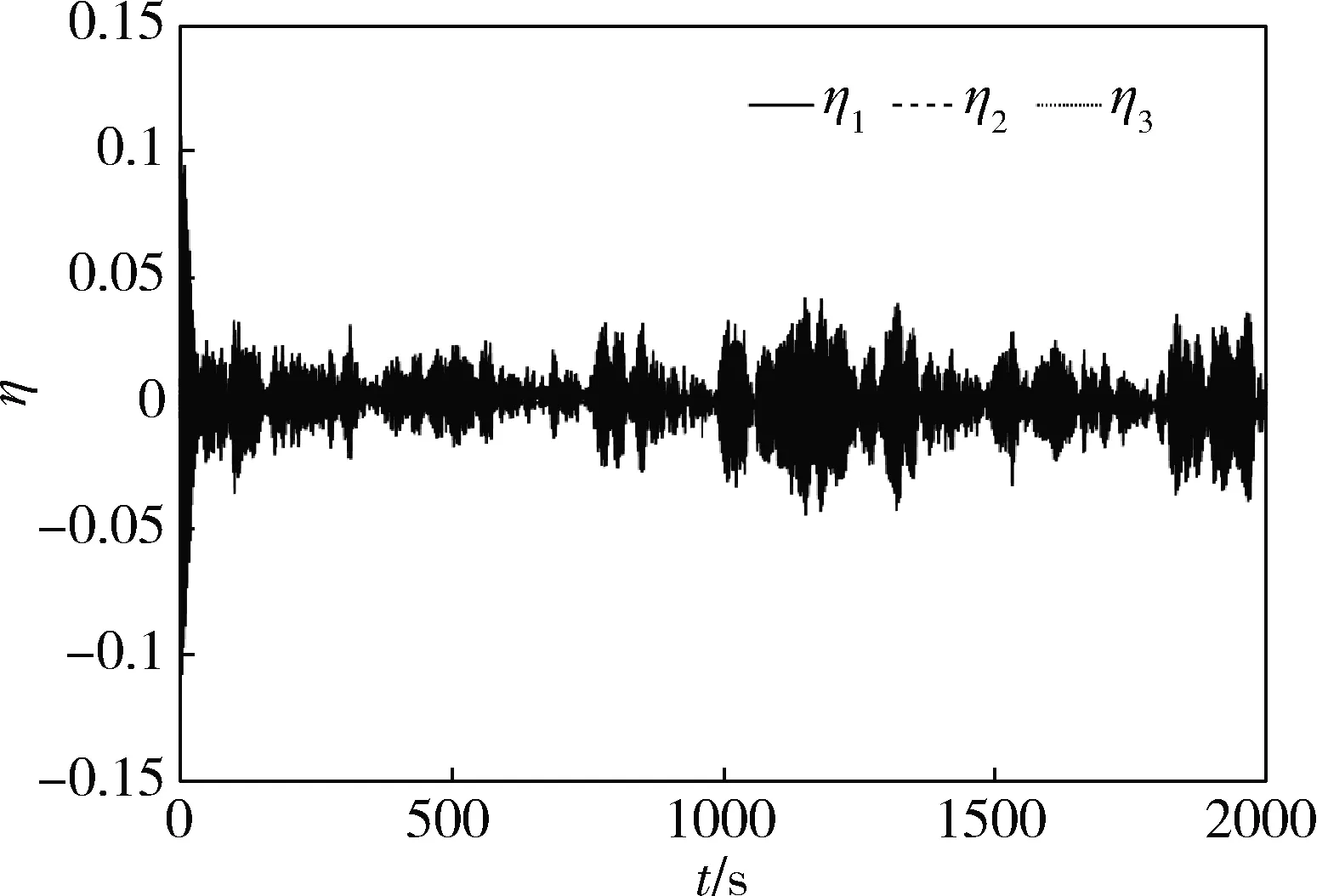
图12 挠性模态变量随时间收敛曲线

图13 挠性模态观测器观测误差曲线

5 结论

通过定义轨迹规划坐标系、姿态规划坐标系、期望绕飞矢量以及期望姿态坐标系，对绕飞过渡过程采用S型速度曲线进行规划，建立了一种新颖的绕飞观测数学模型，实现了服务航天器相对目标从初始位置到任意方位的主动绕飞观测。在此基础上，建立了相对轨道误差动力学模型和相对姿态动力学模型。针对挠性附件的振动模态不可测量问题，设计了基于模态观测器的输出反馈滑模控制律并证明了稳定性。对期望绕飞矢量的引入，实现了对不同绕飞构型的灵活设计，使航天器能够根据任务需求进行不同运动规律的相对运动，对航天器执行在轨服务任务具有参考意义。