大批量订单整体分拣问题建模及其分布式并行方法①

赵云波 李天舒 汪钰皓

(浙江工业大学信息工程学院 杭州 310000)

0 引 言

大型生产和销售需要对大批量订单进行拣取，典型场景可见于大型电商的仓库系统。在较短时间内仓库收到从电商平台产生的大量订单，仓库系统需按照每份订单中包含的商品种类和数量从仓库中拣选货物并打包，随后交付物流系统。这一订单分拣过程的准确性和快速性影响着整体电商流程的效率，已经引起如亚马逊、京东等各大电商的广泛注意，应用了各种尖端技术[1-2]。

常用的订单分拣方式将所有待处理订单中的所有货物归为统一的待拣货集合进行统一处理。系统从仓库货架上依照待拣货集合逐一拣选商品，然后运送至特定地点按照订单进行打包。订单分拣过程分为3个步骤，即货物拣选、货物运送和订单打包[3]。货物拣选大多手工进行，可通过优化物品和货架摆放[4-7]、划分批次等方式提升效率[8-11]。货物运送过程通常可以借由传送带或无人车自动化进行[12]，传送带路线设置、无人车路径规划等是这一步骤效率提升所需考虑的问题[13-16]。订单打包的物理过程较为简单，但其执行依赖于订单中的货物是否可以准确快速到达，这是衡量整个分拣系统效率的标志。

现有订单分拣方式存在的主要问题是大批量订单“整体分拣”能力低。整体分拣是指对任意订单中的货物完整地分拣出来并打包，而不将订单分拆为子订单，每一子订单仅包含所考虑订单货物的真子集。整体分拣是电商系统的天然要求，因为电商的每一个订单都对应唯一一个运送目的地，将一个订单分拆为多个子订单将成倍增加后续物流包裹的数量，增加物流成本。但是，现有订单分拣方式本质上不适应这一整体分拣的要求，其核心原因是对订单打包点的限制。大多数方法的订单打包点都设置为较少的特定地点，比如使用传送带进行已拣选货物的运送，打包点应在传送带的出口(可设置多个出口)；若使用无人车方式进行已拣选货物的运送，作为打包点的运送目的地通常也较为集中，容易导致拥堵和效率低下[17]。现有的对整体分拣的研究，未从根本上解决这一难题[18-19]。在订单分拣问题的研究中，大多关注于具体情境下的设置和算法，缺少描述问题的统一数学框架，导致对这一问题研究不足。

面向上述的大批量订单整体分拣问题缺少严格模型和有效方法的现实，本文首先对该过程进行严格的数学模型化，进而提出一种基于智能货架的分布式并行解决方案。该模型定量描述了整体分拣的静态状态和动态演化，给出了整体分拣问题的明确定义。依托这一模型，提出了相应的解决方案，其核心思想是使用智能货架作为订单分拣点，将订单分拣过程从原先的单一分拣点改造为分布式并行分拣点，从本质上满足了整体分拣的需求。这一改造方式引出了若干技术上的困难，如无人车在不碰撞前提下的高效运行方式，订单的分配方案等。本文在预测控制和优化等框架下对问题进行了有效解决，仿真实验证明了所提出方法的有效性。

本文其他部分组织如下。第1节通过对订单分拣系统的静态状态、动态演化和系统目标等描述，给出了大批量订单整体分拣问题的数学模型。第2节描述所提出的分布式并行整体分拣方法，包括其基本思路、改进模型、关键技术问题和完整算法等方面。第3节利用仿真对比实验证明了所提出的分布式并行方法的有效性。第4节总结全文。

1 大批量订单整体分拣问题的模型化

考虑某一封闭仓库区域H内使用无人车进行货物运送的订单分拣系统。该系统具有如下特点：在任一时刻有大量的订单待处理；每一订单需将其包含的所有货物全部分拣出来并整体打包，不允许进行分拆。本节对这一订单整体分拣问题模型化，首先描述订单系统在任一固定时刻t的静态状态，然后刻画订单系统在时间[t,t+1)内的动态演化过程，最后给出问题的明确定义。

本文中所用符号较多，故将本文所用符号及其含义列为表1。

1.1 订单分拣系统在t时刻的静态状态描述

首先对订单分拣系统在t时刻的静态状态给出符号化描述。这包含货物和货架的状态、待处理订单情况和无人车的状态。

表1 符号列表

货物和货架设该仓储区域内中有Ns个货架，记第i个货架为Si，设货物种类总数为Ng，每一货物以其标识号g为唯一识别，并均存放于某一货架Sg上。记标号为g的货物为Gg，则Gg可表示为

Gg:={g,Sg,Ig}

(1)

其中，Ig为货物Gg在当前时刻的处理状态，定义如下：

(2)

注意其中Ig=0，即“货物在分拣中”的含义是该货物已经交由某无人车运送处理，但尚未取回。

待处理订单每一个订单包含其唯一的订单标识号o，该订单进行整体分拣处理的打包点po，订单到达订单分拣系统的时刻to，和它所包含的所有货物，记该订单为Oo，则：

(3)

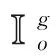
记Io(t)为t时刻所有待处理订单的标识号集合，其个数记为No(t):=|Io(t)|。则t时刻待处理订单的集合可写为

Θ(t)∶={Oo|o∈Io(t)}

(4)

无人车设该仓库区域内有Nv辆无人车用于货物运送。记第i辆无人车为Vi，所有无人车的集合记为V，即：

V∶={Vi|i=1, …,Nv}

(5)

无人车接受货物运送的指令，从相应货架取得货物，并将其运送到目的地。在时刻t的无人车状态由其当前位置、运动情况、承担货物运输情况等信息描述。记无人车Vi在t时刻的状态为Vi(t)，则：

(6)

其中，li(t)、vi(t)和ai(t)分别为无人车Vi的位置、速度和加速度。在笛卡尔坐标系下(假设已经建有原点和x，y轴)，有：

(7)

(8)

(9)

其中，上标x和y分别表示相应向量在x轴和y轴的分量。

由以上定义可知，t时刻空闲的无人车集合VI(t)可计算如下：

i=1,…,Nv} (10)

从而，正在执行某项任务的无人车集合Vo(t)可计算如下：

i=1,…,Nv} (11)

可知，在t时刻订单分拣系统的静态状态可由式(4)中的待处理订单集合Θ(t)和式(6)中的所有无人车的状态Vi(t),i=1, …,Nv完全描述。

1.2 订单分拣系统在[t, t+1)时间间隔内的动态演化

本节定量描述订单分拣系统在[t,t+1)时间间隔内的动态演化。包含新订单的产生过程、订单的处理过程和无人车的运动。注意，[t,t+1)时间间隔的大小主要由无人车的运动情况确定，在该时间间隔内，无人车的运动不会过大而影响算法设计，具体数值需由具体应用确定。

新订单的产生考虑大型电商订单的复杂性，假定订单的到来是随机的。类似情形的随机分布一般建模为指数分布。指数分布假设在很小的时间间隔Δt内，一个新订单到来的概率是λΔt，其中λ是指数分布的强度，即：

Pr{一个新订单在[t,t+Δt)到达}=λ

(12)

由上式可知，[t,t+ 1)时间间隔内新到订单数的期望为λ/Δt。

根据式(3)，新到的标号为N的订单可记为

(13)

(14)

(15)

在具体的订单系统中，可通过调节上述概率κi和ηj描述订单包含货物的数量变化和货物在货架的摆放情况。

同时也需注意，上述新订单产生过程是对真实订单分拣系统的模拟，是为了在数学模型中对该过程进行描述，有利于后续订单分拣方法的设计。而在实际的订单分拣系统运行中并不需要上述模拟过程，新订单是系统实际产生的。

订单的处理在[t,t+ 1)时间内，待处理订单中的货物Gg若被订单分拣系统处理，则其状态会相应发生变化。将货物的状态变化标记为ΔIg，令：

(16)

本文选择的时间间隔足够小，保证了在每一步货物的3种状态最多只能发生一步变化。因此，

Ig(t+1)=Ig(t)+ΔIg

(17)

令co为订单Oo中所有货物的处理状态的最小值，即：

co∶=minIg∈Gg∈OoIg

(18)

注意订单Oo仍待处理的充要条件是该订单中仍有货物未分拣完，即：

(19)

注意co<1包含了co=0和co=-1两种可能。若co=0，则Oo内所有货物都已经安排分拣，但尚有货物还未分拣完成；若co=-1，则Oo内尚有货物未安排分拣。不管是哪种情况，订单Oo都尚未完成分拣。

由此，在[t,t+ 1)时间内处理完的订单集合为

ΘC(t+1)={Oo∈Θ(t)|co(t+1)=1}

(20)

从而，t+1时刻的待处理订单集合可由下式计算：

Θ(t+1)=

(21)

其中，符号“”表示集合的差集。

无人车的运动无人车Vi在[t,t+ 1)内的运动取决于无人车的初始位置li(t)、初速度vi(t)和此时间间隔内的加速度ai(t)。由于[t,t+ 1)很小，可假设在此时间内加速度为常值，即在[t,t+ 1)内有：

(22)

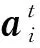
由式(6)可知，无人车在t+1时刻的状态可写为

Vi(t+1)={li(t+1),vi(t+1),ai(t+1),

(23)

其中，ai(t+1)在t+1时刻由算法确定，且：

(24)

(25)

(26)

1.3 大批量订单整体分拣问题

综合1.1和1.2两小节给出的订单分拣系统运行的基本描述。希望设计算法尽可能提升系统的运行效率。在此之前，需要给出算法及其限制条件和运行效率的定量描述。

算法的定义所设计的算法应处理2方面的工作：一方面是将待处理订单中的货物分配给无人车进行分拣和运送；另一方面是协调指挥无人车的运动。

注意到t时刻所有尚需分配无人车进行分拣和运送的货物的集合为

Gg(t)={Gg|Gg∈Oo∈Θ(t),Ig(t)=-1}

(27)

首先，算法将Gg(t)中的货物分配给空闲无人车VI(t)进行运输，即设计如下函数：

fgv:Gg(t)→VI(t)

(28)

而假设函数fgv与时刻t无关。这是因为，上述映射的确定仅决定当前的待处理货物集合Gg(t)和空闲无人车集合VI(t)，而与时刻t无明显依赖关系。

另一方面，算法也需要给出每一辆无人车在[t,t+1)内的运行规则。在已知t时刻无人车Vi的动力学状态前提下(即li(t)和vi(t))，等价于给出在此时间内每一辆运行中无人车的加速度ai(t),Vi∈ VO(t)。从而，所设计的算法具有如下形式：

(29)

限制条件在本文中，限制条件主要指无人车的物理性质及其动力学特性。

无人车所运行的范围、速度和加速度都有其限制，总结如下：

(30)

其中，vmax和amax分别是无人车的速度和加速度上界。本文假定所有无人车都有相同的动力学特性，因此vmax和amax对所有无人车都相同。这在大多数实际系统中是成立的。

无人车在运行过程中不可相互碰撞。定义2辆无人车Vi，Vj间的欧氏距离为

(31)

(32)

其中，d(·，·)表示2点之间的欧氏距离。

任意2辆无人车的距离都不可超过某一事先预定的距离dv，即：

(33)

注意到，由于订单是大批量的，其含有的货物量很大，同时Gg(t)无人车的数量Nv也较大。因此，设计函数fgv(t)较为困难；进一步地，在有限的空间内如何调度所有无人车尽量高速运行而不碰撞也变得异常复杂。

分拣效率的定义订单分拣系统的运行效率可由在统计时域[t,t+Nt)内处理订单或货物的多少来衡量，其中Nt为某正整数，其值的大小表示了统计时域的大小。注意到使用货物或订单的完成量描述分拣效率并不等价，后者更多地与分拣的整体性相关。因此，本文使用在该统计时域内订单分拣系统所完成的订单分拣数量来衡量分拣效率JNt(t)，由式(20)的定义，有：

(34)

综上所述，大批量订单整体分拣问题定义如下。

问题1(大批量订单整体分拣) 给定封闭仓库区域H，式(1)中定义的摆放于Ns个货架上的Ng种货物，式(5)～(11)中定义的无人车集合V及其状态和式(22)～(26)描述的无人车运动方式，式(12)～(15)中描述的新订单产生方式和式(16)～(21)中描述的订单处理过程。在限制条件式(30)～(33)下，设计式(29)中定义的算法A(t)以优化在式(34)中定义分拣效率JNt(t)。

2 大批量订单的分布式并行分拣

面向第1节定义的大批量订单整体分拣问题，本节提出一种基于智能货架的分布式并行解决方法。首先描述该方法的基本思路和硬件要求，进而给出其模型化描述，然后解决其中的关键技术问题，最后给出详细的算法描述。

2.1 分布式并行整体分拣策略及硬件要求

注意到大多数现有整体分拣系统的效率瓶颈在于打包处的稀缺性，本文提出如图1所示的一种新型大批量订单的分布式并行整体分拣模型。该模型的核心要点是允许所有的货架都作为潜在的订单打包处，从而使得订单的打包成为分布式并行的。

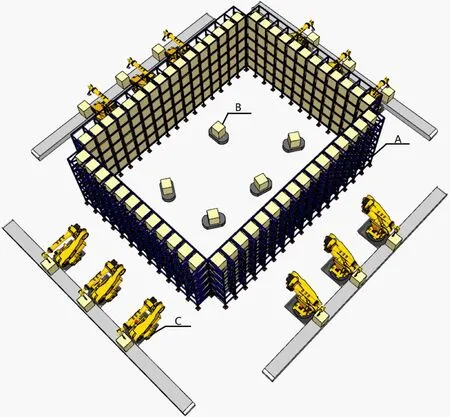
图1 分布式并行分拣模型示意图

在该模型中，将所有Ns个货架首尾相连，其封闭的内部区域作为无人车的运行区域，即H。要求任意2个货架在内H直线可达，无人车在货架内侧取货，并沿直线运送至目的货架。

该模型对现有订单分拣系统的硬件改造主要涉及货架，即原有单纯陈列货物的货架，现其内侧陈列货物，并可将相应货物交付无人车(实现方式可为推取式或机械手[20，21]等)，外侧则改造为订单的打包处。可接收分配的订单。利用无人车从其他涉及的货架上分拣货物，并在订单的所有货物到齐后打包送出。所使用的无人车可以是较为简单的，只需要具有无线通信和运输能力，并能在货架配合下取卸货物即可。

采用该分布式并行分拣模型的分拣流程如下所述：新订单到达后被分配至某一货架打包处处理，利用无人车将订单的所有货物从相关货架中取出并运至该打包货架，待所有货物齐备后完成订单打包任务交给外部物流系统。

2.2 分布式并行整体分拣的模型化描述

本节把在第1节中提出的通用模型针对所提出的分布式并行策略进行具体化(图2)。该策略对一般模型描述的订单和无人车均有影响，详述如下。

2.2.1 分布式并行整体分拣下的订单及其预处理

首先，在分布式并行策略下，订单的打包点是某一货架，因此式(4)中对订单的一般静态定义转化为

(35)

其次，在分布式并行整体分拣下，每一个货架都可以独立接受订单的到来，这意味着式(12)～(15)中新订单产生的描述应理解为对每一个货架适用。从而，式(12)中的新订单产生过程变为

Pr{一个新订单在[t,t+Δt)到达货架Sk}=λk

(36)

式(14)可相应定义。

最后，与式(13)中的一般性表述不同，新到来的订单自动分配至某一货架作为打包点，这就引发了一个自然的预处理过程，即所有已经在该货架上的货物都应该直接可以用来打包，无需再使用无人车运送。也就是说，在分布式并行整体打包框架下，所有[t,t+1)新到来订单都要进行预处理以得到如下新的订单形式。

(37)

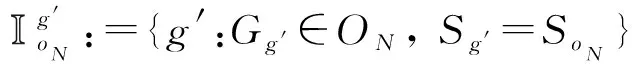
2.2.2 分布式并行整体分拣下的无人车

首先，在分布式并行整体分拣框架下，运行中的无人车在t时刻的位置与一般描述并无不同，但t时刻空闲的无人车Vi∈VI(t)的位置li(t)一定与某一货架相同。在系统运行之后，这一货架即为该无人车上次执行货物运送时所运送货物所属订单的打包点，即：

(38)

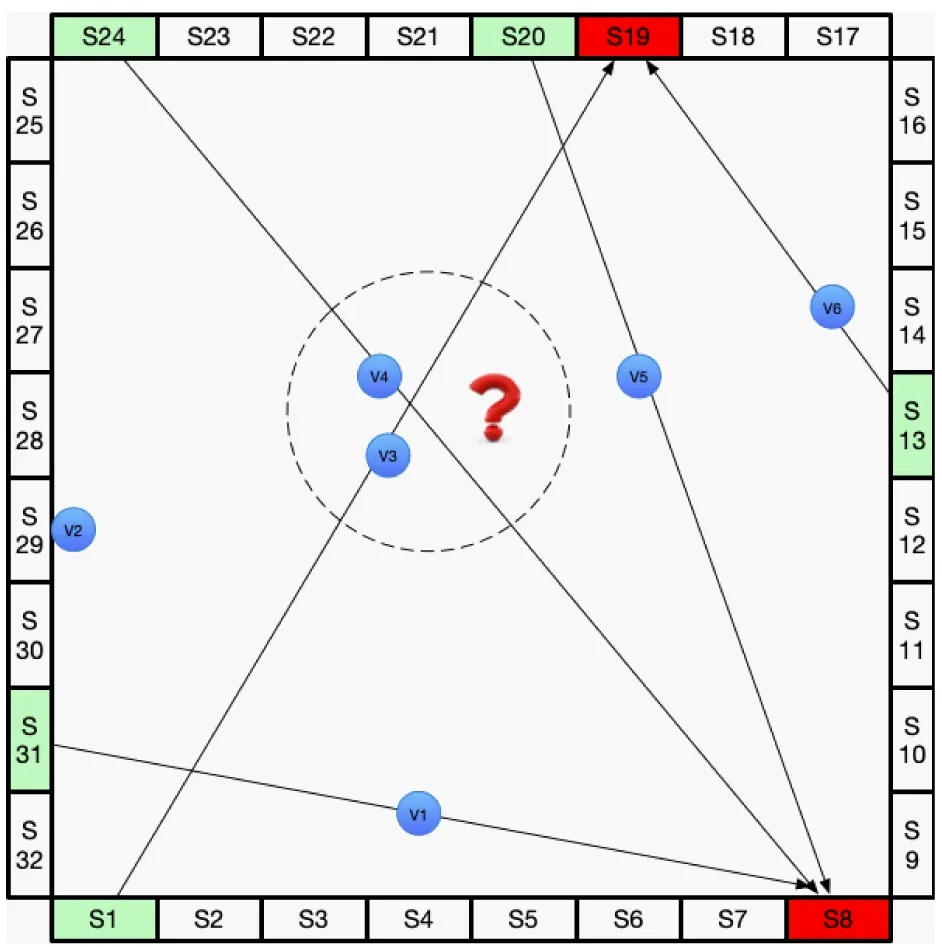
图2 分布式并行分拣方法的模型化示意图

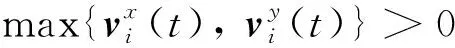
(39)

So=[xo,yo],Sg=[xg,yg]

(40)

因为So和Sg为不同货架，则xg-xo和yg-yo至少有一个不为0。若，记货架So和Sg之间连线与x轴的夹角为θog，则

(41)

进而，如果xg-xo=0且yg-yo≠0，则若yg-yo>0则θog=0，若yg-yo<0则θog=π。

由于vi(t)和ai(t)方向相同(或相反)，无人车在任一时刻从打包货架So到目的货架Sg(未到达目的地前)的行进距离为

(42)

从而，在t时刻无人车Vi的坐标为

(43)

(44)

若无人车是从Sg到So行进，其运行轨迹可类似得到，此时θog=π-θog。

2.3 分布式并行分拣的关键技术问题

2.3.1fgv的构建：优先级优先分配算法

由式(28)定义，fgv将当前待处理货物集合Gg(t)映射到空闲无人车集合VI(t)。在分布式并行整体分拣框架下，fgv的构建应考虑2个重要因素： 待处理订单的完成情况，越接近完成分拣(剩余分拣货物较少)的订单应给予较高处理优先级，这有利于优化式(34)中定义的整体分拣的分拣效率；空闲无人车与打包点距离，货物运送应安排给较近的无人车执行以减小运输距离。

首先，从式(4)定义的待处理订单集合Θ(t)中，计算每个待处理订单Oo中尚需处理的货物数量。

(45)

待处理订单Oo的处理优先级PRIo以如下方法确定。

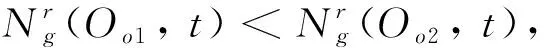
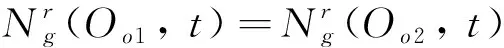
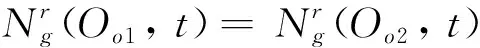
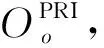
(46)

原先的待处理货物集合Gg(t)变为

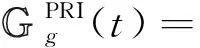
Ig(t)=-1}

(47)

(48)

其中，asc(·)表示将向量按升序排列的函数。

主要从优化订单整体分拣的角度提出如算法1中描述的解决方案，其核心是以货物的运送优先级为先。注意该方法有利于在短期内完成更多的订单，但这个过程可能会使用更多的远距离无人车，从而造成对长期目标的优化不利。如何做到全局优化仍是一个待研究的复杂问题。

算法1 fgv的优先级优先分配算法 输入:t时刻的待处理货物集合GGg(t)和空闲无人车集合VVI(t)。 输出:fgv函数。 (1)由式(45)～(47)计算带有优先级的待处理货物集合GGPRIg(t);由式(48)计算每件待处理货物与空闲无人车的距离向量Dsg; (2)将优先级最高的待处理货物分配给其与无人车的距离向量中的第一个无人车(距离最短); (3)更新空闲无人车信息,将刚分配任务的无人车从VVI(t)中删除;更新所有待处理货物与无人车的距离向量,将刚分配任务的无人车的距离从向量中删除; (4)从剩余待处理货物中选择优先级最高的,重复步骤(2)和(3),直至任一条件满足:1)所有待处理货物全部分配完毕;2)空闲无人车集合为空集。

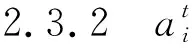
在本文的分布式并行整体分拣框架下，无人车的所有运动决策都由某中心控制器给出。这一决策的核心是给出[t,t+1)内每辆运行中无人车的加速度。

从单独一辆无人车的角度看，为了使其运行效率最高，应该使其一直在最高速度运行。但多辆无人车在限定区域H中交叉运行，如果不进行限制不可避免会遭遇碰撞。按式(33)中的要求，Vi、Vj发生碰撞即二者之间距离小于某预定dv。注意到为了整体的效率优化，考虑在多步运行后的无人车状态：如果让某无人车在[t,t+1)内保持高速运行会极大提高在此后与其他无人车碰撞的可能，限制其在[t,t+1)内的运行速度，而这是只考虑在[t,t+1)内的运动无法得到的。为了系统运行的整体最优，需要预测系统很多步后的可能运动状态，并从中选取合适的运动序列，但这种对未来轨迹的预测对计算能力有很高的要求，这一原因促使本文中做了2个决定：一方面，系统架构中采用中央控制器进行每辆无人车的路径规划，不允许每辆无人车自主规划；另一方面，在路径规划上，采用如下的模型预测控制策略，以有限步长的滚动优化来决定无人车的运动。

由式(7)可得：

由上式并注意到无人车不会倒向行驶且一直保持直线行驶，无人车Vi在[t,t+T)内的运动总长度Li[t,t+T)为

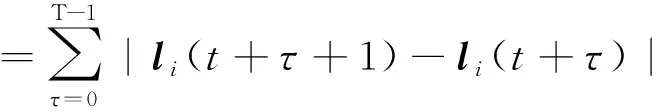
(49)

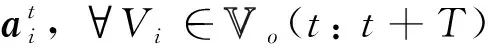
(50)

(51)

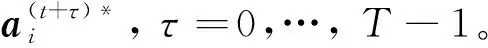
(52)

2.4 分布式并行整体分拣框架和算法

算法2 分布式并行整体分拣算法 输入:t=0, Ns个货架的位置,待处理订单集合Θ(0)=Ø,无人车集合VV=VVI(0),VVo(0)=Ø,及其初始状态Vi(0), Vi∈VV。 输出:订单的整体分拣运行。 在t时刻, (1) 按式(12)～(15)和式(35)～(37)产生新订单并更新待处理订单集合,按式(2)更新待处理货物集合; (2) 按式(45)～(48)和算法1确定fgv函数,按(13)确定ati, Vi∈VVo(t); (3) 按式(22)～(26)更新无人车状态,按式(16)～(21)更新待处理订单集合,按式(27)更新待处理货物集合; (4) 令t=t+1。

3 仿真算例

考虑封闭仓库区域H为长宽各为50 m和45 m的方形区域，将笛卡尔坐标系的坐标原点建于其中某顶点，x轴和y轴各沿方形的一边，如图3所示。

其中菱形表示某订单的打包所在货架，五角星表示某待

在仿真中,设货架数Ns=88，无人车数量N=20，在仿真开始的初始位置是随机确定的。式(36)中新订单的到达强度λk=0.23，∀k=1,…,Ns，式(14)中κ=0.1，ηj=1/88。无人车的速度和加速度约束为vmax=3 m/s，amax=2 m/s2，任意2辆无人车的距离都不可超过某一事先预定的距离dv=3.15 m。

其中菱形表示订单的打包口，五角星表示某待取货

考虑Nt=1时的分拣效率J1(t)，即在单位时间[t,t+1)内所完成的订单数。其演化规律在4种方法下的比较见图5。从中可以看出，采用分布式整体分拣方式的分拣效率比常规分拣方法高出3倍。这一效率提升的原因可从分布式并行分拣允许多个订单打包点的本质特点解释。

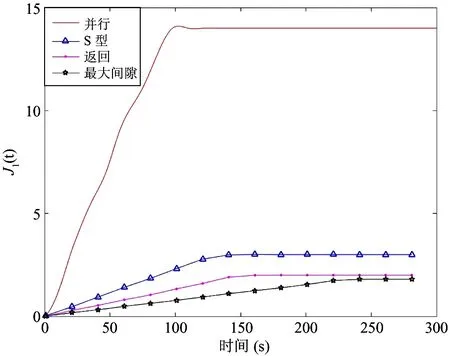
图5 在统计时域[t, t+1)内，4种分拣方法的分拣效率J1(t)随时间的演化规律图

这4种分拣方式在系统初装和运行成本上的差别主要在无人车方面。常规方法的无人车一般需要有相当的自主能力，如避障等能力，而本文所提出的分布式整体策略的无人车则可以简化，只要可接受指令行进即可。分布式整体方法需要对货架进行一定改造，但原先货架若允许无人车分拣也应已经具有一定智能，添加打包点能力的改装并不额外增加太多成本。因此总体上来说，分布式整体分拣方法的初装和运行成本也可以有一定降低。

4 结 论

大批量订单的整体分拣是物流系统中的一个重要问题，其效率提升对整体物流效率的提升至关重要。本文提出的分布式并行模式的整体分拣策略和方法利用多打包点的想法，使用优先级订单分发和基于预测的无人车动态规划等技术，提升了订单分拣系统的整体分拣效率，具有较好的潜在应用价值。本文研究较为初步，在后续研究中，还需要在货架摆放、货物摆放、高效算法即fgv和ai(t)的确定等方面做更为深入的研究。