基于模型预测控制的水下机器人动态目标跟踪控制①
魏亚丽 朱大奇 褚振忠
(上海海事大学智能海事搜救与水下机器人上海工程技术研究中心 上海 201306)
0 引 言
水下动态目标跟踪技术在海洋资源勘探、水下工程作业、海战场监视及水下精确制导等方面具有广泛的应用前景。近年来,水下动态目标跟踪问题研究得到了一定的发展,在声纳图像处理及动态目标定位方面提出了很多方法。文献[1]提出了基于声纳图像的高斯混合基数化概率假设密度(Gaussian mixture cardinality probability hypothesis density,GM-CPHD)滤波算法,更有效地实现了目标状态及数目的估计。文献[2]提出了基于鲁棒粒子滤波的被动声纳多目标跟踪算法,该算法能够在保持多目标连续跟踪的同时跟踪未知的时变多目标,提高了水下目标跟踪的准确性。文献[3]针对主动声纳测量误差引入的目标机动决策模糊问题,提出了一种基于机动检测延迟的跟踪滤波算法,提高了声纳图像目标定位的精度。文献[4]研究了基于交互式多模型的水下动态目标跟踪问题,在动态目标轨迹预测中具有较好的实时性与可靠性。以上相关研究成果大多关注于水下动态目标识别与预测问题,而对动态目标轨迹跟踪控制这一核心问题较少研究。
本文研究基于水下机器人的动态目标跟踪控制问题,利用前视声纳图像对动态目标进行实时定位,并通过无迹卡尔曼滤波器预测动态目标轨迹;在此基础上,提出一种基于模型预测控制(model predictive control,MPC)的水下机器人动态目标跟踪控制方法。最后,通过水池实验与仿真分析对所提方法进行有效性验证。
1 水下动态目标跟踪系统
本文探讨结合多波束前视声纳的水下机器人的动态目标跟踪控制问题,所构建的水下机器人动态目标跟踪系统主要由水下目标定位与轨迹预测以及水下机器人动态目标跟踪控制2个部分组成。
(1)水下目标定位与轨迹预测
基于多波束前视声纳实时提供的水下动态目标图像,通过开运算、阈值分割和特征处理等方式,完成水下目标识别与定位。考虑到拟跟踪目标是处于动态变化中的,本文构建无迹卡尔曼滤波器,通过时间窗滚动的方式预测下一时刻的水下动态目标轨迹信息。
(2)水下机器人动态目标跟踪控制
在预测得到下一时刻的目标位置后,设计控制器使水下机器人跟踪预测目标位置运动。为此,本文利用模型预测控制算法,经过在线滚动优化和反馈校正,产生水下机器人期望的速度与期望航向角信息。通过跟踪该期望速度与航向角,最终完成水下动态目标的跟踪控制。
2 水下目标定位与轨迹预测
如图1所示,多波速声纳采集到的水下动态目标图像是以亮斑形态出现的[5]。除拟跟踪的动态目标之外,还存在鱼、海藻、垃圾等其他物体。在滤波去噪的基础上,还要进行形态学处理以去除小的干扰物。本文利用开运算的效果除去图像中的小目标而保持大目标的形状和大小不变[6]。其定义如下
(fοq)(x,y)=(fΘq)⊕q
(1)
其中,f为二值图像原图,q为结构元素,(x,y)为结构元素所在的二值图像中的连通域,即对图像先进行腐蚀操作,然后进行膨胀操作的运算过程[7]。
图1为一幅水下目标的声纳图像,图像中除拟跟踪动态目标之外还存在较多小的亮斑区域。当外部干扰较多时,亮斑会更多[8]。本文结合所采用的多波束声纳特性,提出了一种阈值分割和特征提取相结合的方法。针对声纳的阈值分割问题,设置阈值T1、T2、T3,阈值分割方法如式(2)所示。若阈值小于T3这个大小的区域则自动填充为黑色,而阈值在T1到T2之间的区域则保留下来。

图1 水下动态目标声纳图像
ck={0,|l>T1,l (2) 其中ck为阈值分割后的保留区域,l为被检测位置的阈值大小。 考虑到声纳可视区域内可能会存在除目标之外的杂物和其他干扰信息,本文还引入了特征提取,其目的在于对亮斑形状进行提取。对于满足拟跟踪目标形状的亮斑,在满足阈值范围的前提下选择出来并标记出重心位置。标记出目标位置后,计算目标在声纳二值图像中的坐标位置。假设目标位置为(X,Y),同时计算声纳二值图像的大小,设其为(N,M)。根据声纳反馈数据可知实际探测最大距离为r,而图像中点和扇形中点是同一位置。在二值图像中点的纵向坐标值为M/2,实际位置纵向坐标为r/2,因此实际的位置坐标与声纳二值图的坐标比例为r/M。于是,可知任意位置二值图像坐标(X,Y)转换到实际坐标系中的大小为(X×r/M,Y×r/M)。 由于拟跟踪目标位置是动态变化的,若直接以当前时刻的目标位置为参考点进行跟踪控制,则很难完成。为此,在获得水下动态目标当前时刻的位置信息后,本文利用无迹卡尔曼滤波器进行目标位置预测。由于目标运动是非线性的,普通卡尔曼滤波是对非线性的系统方程或者观测方程进行泰勒展开,这样不可避免地引入了线性化误差[9]。而无迹卡尔曼滤波摒弃了对非线性函数线性化的传统做法,对于一步预测方程使用无迹变换来处理均值与协方差的非线性传递问题[10],提高了估计的精度,稳定性更好。本文所构建的动态目标轨迹预测系统的输入是每个当前时刻的动态目标的位置信息,其输出是经过无迹卡尔曼滤波器预测得到的下一时刻的动态目标的轨迹信息,用来作为水下机器人动态跟踪的设定值。 模型预测控制算法是现在应用范围广泛的控制算法。该算法对模型的精度要求不高,建模方便,采用了非最小化描述模型,系统的鲁棒性、稳定性较好。此外该算法能有效地处理多变量多约束的问题,这些特别适合航行速度较慢、模型精确度不高的水下机器人系统[10]。模型预测控制算法实现时有3个关键步骤,分别是预测模型、滚动优化和反馈校正[11]。 通过无迹卡尔曼预测得到水下动态目标下一时刻的轨迹信息后,采用模型预测控制算法设计水下机器人的期望速度与期望航向角信息以实现动态目标跟踪控制。本文构建的水下机器人动态目标跟踪控制器如图2所示。控制器主要由误差模型、系统约束以及目标函数组成。误差模型就是目标跟踪控制系统的数学描述,也是构建控制算法的基础[12]。本文中的误差模型就是实时控制的水下机器人的位置与动态目标位置的差值。为了防止模型失配引起控制对理想追踪的偏离,在新的采样时刻,会先检测误差大小,并利用这一信息对模型的预测结果进行修正然后再进行新的优化,这也就是反馈校正的过程[13]。系统约束包括水下机器人的速度约束、控制量平滑约束以及稳定性约束。目标函数的设计则综合考虑目标跟踪的快速性与平稳性。并且模型预测的控制优化不是一次离线进行的,而是反复在线进行的滚动优化[14]。 图2 水下机器人动态目标跟踪控制器 假设水下机器人的重心与浮心距离够远,则可忽略水下机器人的纵倾运动与横倾运动。水下机器人惯性坐标系与载体坐标系下运动状态向量分别为η=[x,y,z,ψ]T和v=[u,v,w,r]T,其中x、y、z、ψ分别表示水下机器人在大地坐标系下的x方向位置、y方向位置、z方向位置和艏向角,u、v、w是线速度矢量在载体坐标系中的3个分量。r是角速度矢量在载体坐标系中的一个分量。水下机器人的运动学方程可表示为 (3) (4) 为了能将该模型应用于模型预测控制器的设计,需要对式(4)进行离散化处理,得到: (5) 在模型预测控制构建的目标函数中,需要计算未来一段时间系统的输出[15]。因此,对式(5)进行变换,得到: (6) 从而,可进一步得到新的状态空间表达式为 (7) (8) 为了简化后续的分析计算,假设: Ak,τ=At,t,k=1,…,t+Ν-1 Bk,τ=Bt,t,k=1,…,t+Ν-1 则,推导可得到预测的输出为 Y(t)=Ψtξ(t|t)+ΘtΔV(t) (9) 其中, Θt= 式(9)中,预测的状态量和输出量都可以通过当前状态量和控制增量计算得到。为实施模型预测控制,需构建二次规划优化问题[16]。 在实际的水下动态目标跟踪过程中,由于水下机器人动力系统对于控制量跳变要求比较严格,因此本文将控制增量作为目标函数的状态量,所构建的优化目标函数为 (10) 其中,Np为预测时域,Nc为控制时域。 式(10)中,第1项反映了水下机器人对于动态目标的跟踪能力,第2项反映了对控制量平稳变化的要求。Q和R是权重矩阵。另外,在实际的控制系统中往往还需要满足系统一定的约束条件,具体为 控制量约束: νmin(t+k)≤ν(t+k)≤νmax(t+k) (11) 控制增量约束: Δνmin(t+k)≤Δν(t+k)≤Δνmax(t+k) (12) 其中,k=0,…,Nc-1。 将式(7)代入式(10),可得完整形式的目标函数: J(ξ(t),ν(t-1),ΔV(t)) =ΔV(t)HtΔV(t)T+GtΔV(t)T (13) 其中, 因此,模型预测控制在每一步的带约束优化求解问题都等价于求解如下的二次规划问题: k=t,…,t+Hc-1 ΔVmin≤ΔV(k)≤ΔVmax,k=t,…,t+Hc-1 (14) 在每个控制周期完成对式(14)的求解后,得到了控制时域内的一系列控制输入增量。本文所构建的目标函数是一个典型的二次规划优化问题,且具有线性与非线性约束条件。在每个控制周期内完成对目标函数的求解后,利用得到的控制时域内的一系列控制输入增量。根据模型预测控制的基本原理,将该控制序列中第一个元素作为实际的控制输入增量作用于系统,系统执行这一控制量直到下一时刻,循环往复,直至系统完成动态目标跟踪控制。 为验证本文所设计的水下动态目标定位与轨迹预测系统的有效性,利用多波束前视声纳在校内河流中进行了实验。实验中水下动态目标采用遥控水下机器人进行模拟,机器人outland1000(ROV)尺寸为0.65 m×0.37 m×0.26 m。图3是outland1000的外观图,图4为校内实验场景图。 图3 目标机器人实物图 图4 校内实验场景图 多波束前视声纳获取图像后上传至计算机。图5(a)为声纳原始图像,可以看出图中有很多的噪声点和其他干扰物。图5(b)是灰度化和滤波后的图像。图5(c)是形态学操作和阈值处理后的图像,可以看出小的物体已经被去除,只有较大的亮斑被保留。根据跟踪目标的亮斑区域大小,将阈值分别设置为2 000(T1)、4900(T2)和420(T3)。对于小于阈值T3的自动填充为黑色,同时把介于T1和T2间的区域保留下来。图5(d)是特征提取部分。由于模拟的水下动态目标(ROV水下机器人)为一长方形物体,因此通过判断亮斑区域是否为长方形,即可完成目标识别。在找到长方形亮斑区域后,标记出轮廓重心在图像区域中的位置。结合多波束前视声纳所反馈的探测范围数据,可解算出动态目标相对于水下机器人的位置坐标,即实现水下动态目标定位。 图5 声纳图像处理 本文的动态目标运动是非线性的,无迹卡尔曼使用无迹变换来处理均值和协方差的非线性传递,是对非线性函数的概率密度分布进行近似,用一系列确定样本来逼近状态的后验概率密度,而不是对非线性函数进行近似,不需要求导计算雅可比矩阵,没有线性化忽略高阶项,因此无迹卡尔曼非线性分布统计量的计算精度较高。表1是无迹卡尔曼滤波及卡尔曼滤波预测出的动态目标位置和真实位置的坐标,真实位置数据是在水池实验中采集的。图6是2种预测算法的轨迹误差对比图,其中虚线为卡尔曼预测结果,实线为无迹卡尔曼预测结果。从数据和误差图中可以明显看出无迹卡尔曼的预测更加准确。其中卡尔曼预测x轴的最大误差值是2.03 m,平均误差值为0.995 m。而无迹卡尔曼预测的x轴最大误差为0.62 m,平均误差为0.31 m。卡尔曼预测y轴坐标最大误差为1.96 m,平均误差为1.063 m。无迹卡尔曼预测y轴最大误差为0.37 m,平均误差为0.22 m。卡尔曼预测z轴最大误差值为2.87 m,平均误差值为1.356 m。无迹卡尔曼预测z轴最大误差值为1.27 m,平均误差为0.39 m。图7是目标预测结果对比图,标注△的曲线为实际坐标位置,标注▭的曲线为卡尔曼预测位置,标注▽的曲线为无迹卡尔曼预测位置。从图中可以证明出无迹卡尔曼预测数据比卡尔曼预测稳定性好,估计精度高。上述实验中,虽然遥控水下机器人模拟的动态目标运动具有很大的不确定性,但所设计的目标定位与轨迹预测系统能够获得较好的精度,为水下动态目标的跟踪控制提供了保证。 表1 真实数据与预测数据 图6 轨迹预测误差对比 图7 目标预测结果对比 为验证所提基于模型预测控制的水下机器人动态跟踪控制方法的有效性,分别在2维环境及3维环境下进行了仿真验证。 在水下机器人动态目标跟踪控制中,将动态目标的预测轨迹点作为期望跟踪点。模型的误差为水下机器人追踪位置与动态目标实际位置的差值。速度控制约束为[-2 m/s, 2 m/s],角速度约束为[-0.7 rad/s, 0.7 rad/s]。模型预测的参数Q=[1 0 0 0;0 1 0 0,0 0 1 0;0 0 0 0.5],R=[0.1 0 0 0;0 0.1 0 0;0 0 0.1 0;0 0 0 0.1]。 图8为2维环境下模型预测控制与反步控制的仿真对比结果,2维起始点为(9,15),从仿真结果可以看出2种控制算法都能达到跟踪动态目标的效果。模型预测的跟踪效果与反步控制相比,控制精度高,更加稳定。图9为2种控制算法的误差对比图,从图中也可以看出,反步控制的误差要比模型预测控制的大很多,稳定性也要差一些。由于反步控制算法中没有加入速度变化约束,所以导致速度变化很大,造成跟踪效果的不稳定。与反步相比,模型预测控制算法加入了速度变化约束,使速度的变化量控制在正负2 m/s之间,进而提高了跟踪的稳定性。图10为模型预测控制的控制输出量,从图中可以看出,模型预测控制的速度输出量都在速度变化约束之间。 图8 2维跟踪对比结果 图9 2维跟踪误差 图10 2维模型预测控制输出 图11为3维环境下基于模型预测控制与反步控制的仿真对比结果。3维起始点为(5,13,9),从仿真图可以看出,无论是模型预测控制还是反步控制的跟踪趋势都是符合动态目标的运动趋势的。但是模型预测控制的跟踪效果与2维情况相同,明显比反步控制的跟踪控制精度高,更加稳定。图12为3维环境下的动态目标跟踪误差,即水下机器人实际轨迹与动态目标预测轨迹的偏差。表2是2种控制算法在3维情况下不同坐标轴的误差数据。从表中可以看出,模型预测控制算法在每个坐标轴的误差均值都要小于反步控制算法。由于反步控制算法中没有加入速度变化约束,所以导致速度变化很大,造成跟踪效果的不稳定。与反步相比,模型预测控制算法加入了速度变化约束,使速度的变化量控制在±2 m/s之间,进而提高了跟踪的稳定性。图13为3维环境下模型预测控制算法产生的控制量,从图中可以看出水下机器人的期望速度与期望角速度均在设定的约束范围内。正因如此,模型预测控制算法的速度变化不会像反步那么剧烈,并且模型预测控制对于水下机器人的模型要求不高,所以模型预测控制算法的跟踪精确度和稳定性比反步算法高。以下的仿真结果均能证明,所提出的模型预测控制算法具有较好的跟踪控制能力,在水下机器人动态目标跟踪控制中是可行的。 图11 3维跟踪对比结果 图12 3维跟踪误差 表2 跟踪误差均值 图13 3维模型预测控制输出速度 本文探讨了水下动态目标的定位与轨迹预测方法,提出了一种基于模型预测控制的水下机器人动态目标跟踪控制方法。基于多波束前视声纳的实验结果表明,所提方法在水下动态目标的识别、定位与轨迹预测中具有较高的精度。但是本文只在运动学模型中进行了仿真实验,还未扩展到动力学模型中进行实验,模型预测控制的优化算法还可以作进一步的改进,使跟踪效果更加精确,这也是下一步需要研究的工作。3 水下机器人动态目标跟踪控制

3.1 水下机器人模型



3.2 模型预测控制






4 实验与仿真
4.1 水下目标定位与轨迹预测实验




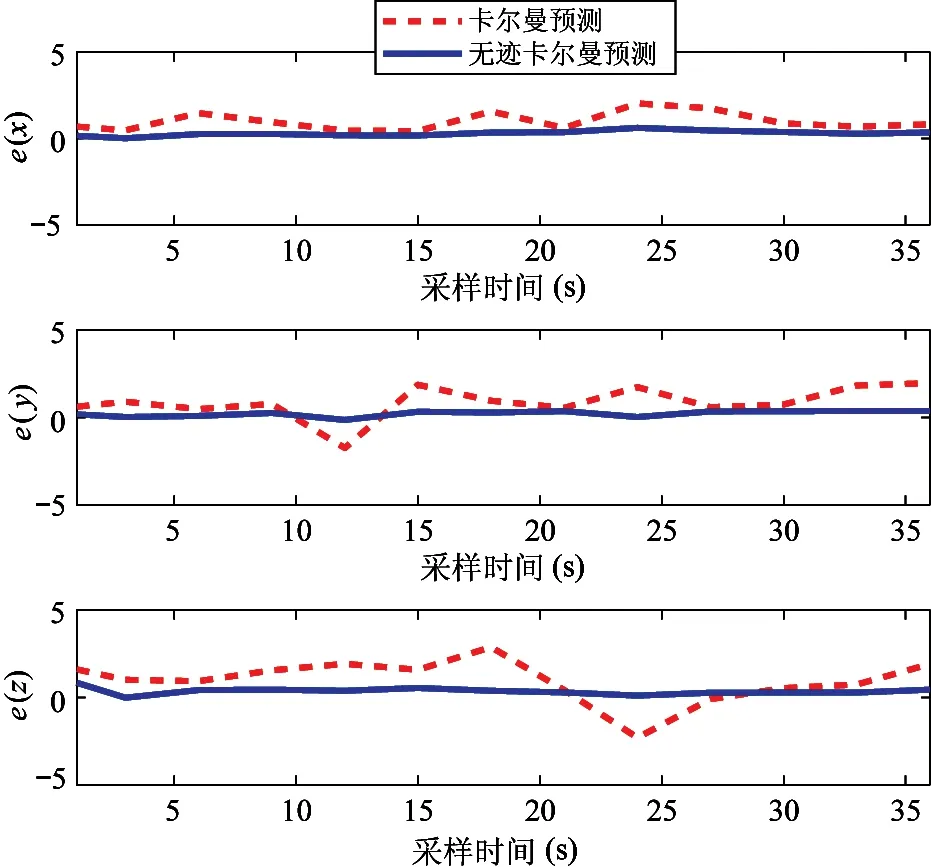
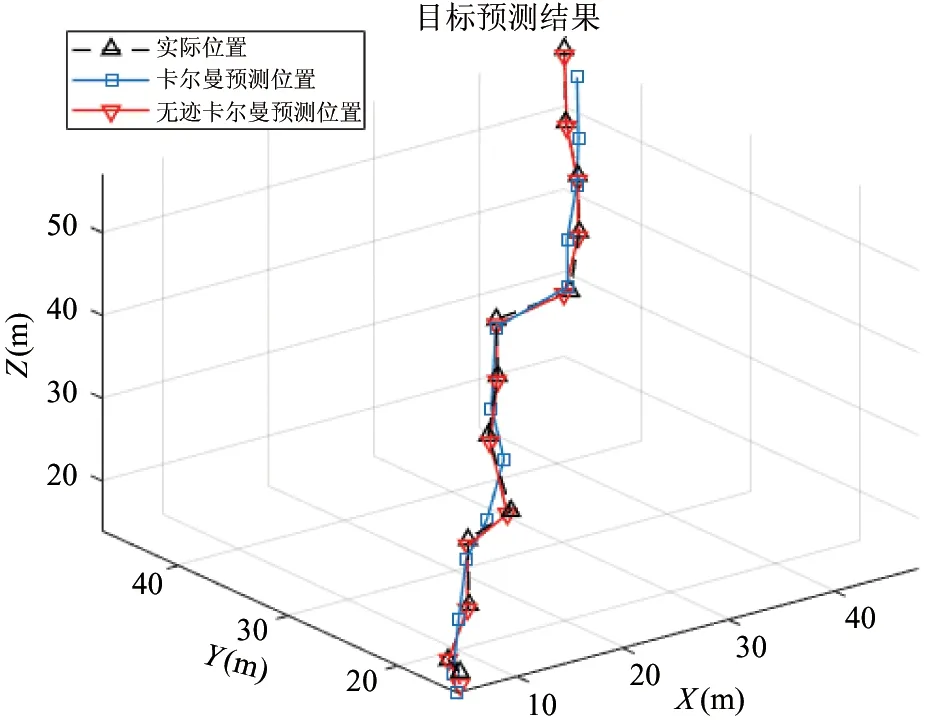
4.2 水下机器人动态目标跟踪控制仿真
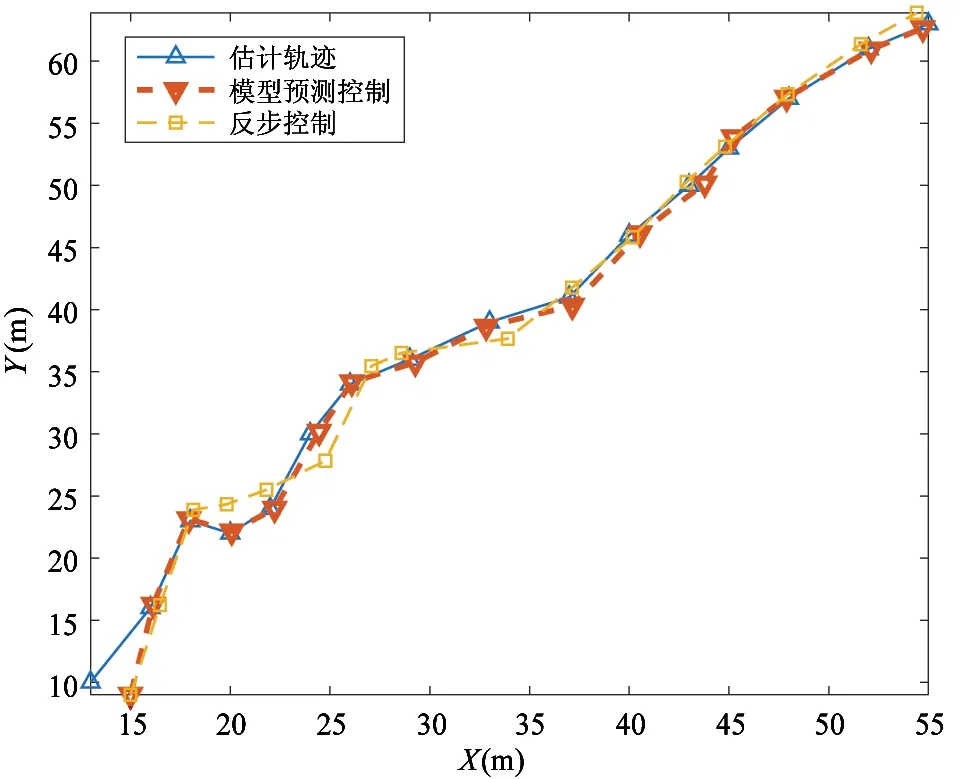






5 结 论

