ECO跟踪算法中CNN分层插值及加权策略改进①
陈志旺 王昌蒙 王 莹 宋 娟 彭 勇
(燕山大学工业计算机控制工程河北省重点实验室 秦皇岛 066004)(燕山大学国家冷轧板带装备及工艺工程技术研究中心 秦皇岛 066004)
0 引 言
目标跟踪的主要任务是给定视频序列中的第一帧目标的初始状态(目标位置、目标框尺度),在后续的视频序列中去估计目标新的运动轨迹或状态,它是计算机视觉中的一个基础问题。目标跟踪技术已经广泛应用在安防监控、人机交互、机器人、军事侦查、智能交通[1]等领域,其实用价值日益增强。经过多年的研究,目标跟踪技术已经有了长足的发展和进步,但依旧面临着很多复杂环境下的挑战,如目标外形变化、光照变化、遮挡、背景复杂等,这些因素都将导致目标漂移甚至跟踪失败。
跟踪方法可以分为基于生成模型的跟踪和基于判别模型的跟踪。生成模型跟踪方法应用特征空间来描述目标,学习一个有代表性的目标模型,利用该模型去搜索图像区域,按照模式匹配的方法,在图像中找到和该模型最匹配的区域即为目标。比较典型的例子有均值漂移Meanshif[2]、粒子滤波Particle Filter[3]和L-K光流算法[4]。判别模型将跟踪看成一个二分类问题,由构建的正负样本训练最优分类面,把目标和背景在图片中区分开来,将分类器置信度最大的位置作为检测到的目标位置。基于支持向量机[5](support vector machines,SVM)的方法,基于随机森林[6](random forest,RF)分类器的方法都是判别模型跟踪方法的代表。近几年,相关滤波理论被应用于判别模型跟踪算法中,取得了较好的跟踪效果。
2010年,Bolme等人[7]提出了最小均方误差输出和(minimum output sum of squared error, MOSSE)相关滤波器,首次将相关滤波应用到目标跟踪算法上,应用灰度等级图像提取单通道特征图,在训练和检测过程中利用相关滤波的性质,将时域的卷积操作转化为频域的点乘,使计算效率大大提高。2014年,Henriques等人[8]把核技巧引入到脊回归中,提出了核相关滤波器(kernelized correlation filters,KCF)目标跟踪算法,应用核函数把低维空间不可分地映射到高维核空间变为线性可分,应用循环矩阵进行正负样本采集,由于循环矩阵在傅里叶空间可对角化,所以可将复杂的矩阵运算转化为元素的点乘,提高了运算速度,同时利用脊回归训练目标检测器,进一步提升了跟踪算法的性能。此后,很多研究者基于KCF跟踪算法进行了改进,大量论文相继发表出来。胥方等人[9]针对核相关滤波(KCF)算法对快速移动目标跟踪中由于边界效应导致误差跳动与跟踪丢失的问题,提出了基于核相关滤波的自适应跟踪算法。Danelljan等人[10]利用颜色(color-names,CN)特征来构建目标外观特征,将RGB三通道的颜色转换成11 种颜色特征,使用主成分分析[11](principal components analysis,PCA)将11维特征降至2维,得到目标低维颜色特征,然后选择最为明显的颜色作为目标特征进行跟踪。文献[12]设计了2个相关滤波器,一个2维的位置滤波器和一个1维的尺度滤波器,分别实现目标的位置跟踪和目标尺度变换,STAPLE算法[13]提出一种融合算法,用方向梯度方图(HOG)特征和颜色直方图特征2种互补的特征因子对目标进行学习,融合跟踪算法,在跟踪速度有所提高的同时,也保证了跟踪效果。张立国等人[14]考虑到应用环境复杂,跟踪算法对光照变化鲁棒性不强,导致目标跟踪时数据丢失、实时跟踪时检测速度不够等问题,结合哈希指纹特征对光照变化鲁棒性强的特点,提出一种多尺度(multi-scale)感知哈希(Hash)特征的目标跟踪算法,即Mhash算法。
随着深度学习在视觉分类和检测领域获得突破性的进展,由于其强大的特征学习能力使其在跟踪领域也逐渐得到重视。DLT[15](deep learning tracking)是第一个在目标跟踪算法中引入深度学习的方法 。随后,越来越多的深度神经网络模型,如自动编码机[16]、卷积神经网络[17](convolutional neural networks ,CNN)、循环神经网络[18](recurrent neural network,RNN)、孪生(siamese)网络[19]等都被应用到了目标跟踪领域,并在跟踪效果上取得了较好的绩。用于跟踪的高效卷积运算符(efficient convolution operators for tracking,ECO)[20]是C-COT[21]的改进版本,C-COT在OTB100[22]上获得了较好的效果,并且在VOT2016[23]获得了第1名,ECO在C-COT的框架上旨在通过解决计算复杂度和过拟合问题来同时提高速度和跟踪效果。文献 [24]在ECO的基础上,只用CNN提取的特征,将CNN的浅层特征和深层特征进行融合,使追踪器具有较好的性能。Bhat等人[25]通过分析浅层特征和深层特征的特征差异,提出两种特征分而治之,深层特征部分加入了数据增强,增加训练样本数量,两部分响应图自适应融合,得到最优的目标定位结果。STRCF算法[26]将空间正则化和时间正则化应用到判别相关滤波(discriminative correlation filter,DCF)框架中,使算法对目标遮挡具有很强的鲁棒性,并且能很好地适应目标较大的外观变化,应用交替方向乘子法(alternating direction method of multipliers,ADMM),在不降低效率的情况下提高了跟踪的准确性和速度。
本文在ECO算法的基础上,为了提高算法的跟踪速度,CNN提取的特征图进行插值处理时采取分层插值,分辨率较高的浅层特征不插值,分辨率低的深层特征插值,以此降低插值操作带来的复杂运算,提高跟踪速度;在生成样本空间策略上,保留了所有的样本信息,使训练样本集有更丰富的多样性,并且考虑到每个特征层的权重不同对样本的分类会产生影响从而影响跟踪效果,为不同特征层分配了不同的权重;为了能更好地应对目标尺度的变换,应用文献[12]提出的1维尺度滤波器对目标尺度变换进行估计,把尺度的候选数从ECO算法中的5个增加到33个,使尺度估计更加鲁棒。
1 ECO算法介绍
1.1 连续卷积算子

(1)
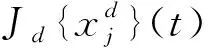
通过学习一个线性卷积算子Sf{xj},该算子通过寻找图片区域中最大置信分数来估计新一帧目标位置,在连续域方程中,算子Sf{xj}是由一系列卷积滤波器f=(f1,f2,…,fd,…,fD)构造出的,定义卷积算子为
(2)
这里*表示卷积运算,下同。每个特征通道首先用式(1)进行插值操作,然后和对应的滤波器卷积,最后所有卷积响应加起来产生最终的置信函数Sf{xj}。
每个训练样本xj由卷积算子的期望输出yj所标定,所以相关滤波器的损失函数公式为
(3)
式中,αj表示每个训练样本的权重,w是空间正则化惩罚项,M表示训练样本的个数,通过最小化函数式(3)来训练滤波器f。
虽然C-COT算法在跟踪效果上取得了非常好的效果,但是该算法模型参数多,需更新的参数达800 000个,这么多参数除了速度慢,还容易引起过拟合;C-COT生成训练样本集的方法是把每一帧的跟踪结果放在一个训练集中,这样随着视频越来越长,训练集就会越大,在更新模型时还是容易过拟合。
1.2 因式分解卷积操作

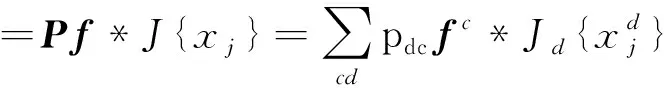
=f*PTJ{xj}
(4)
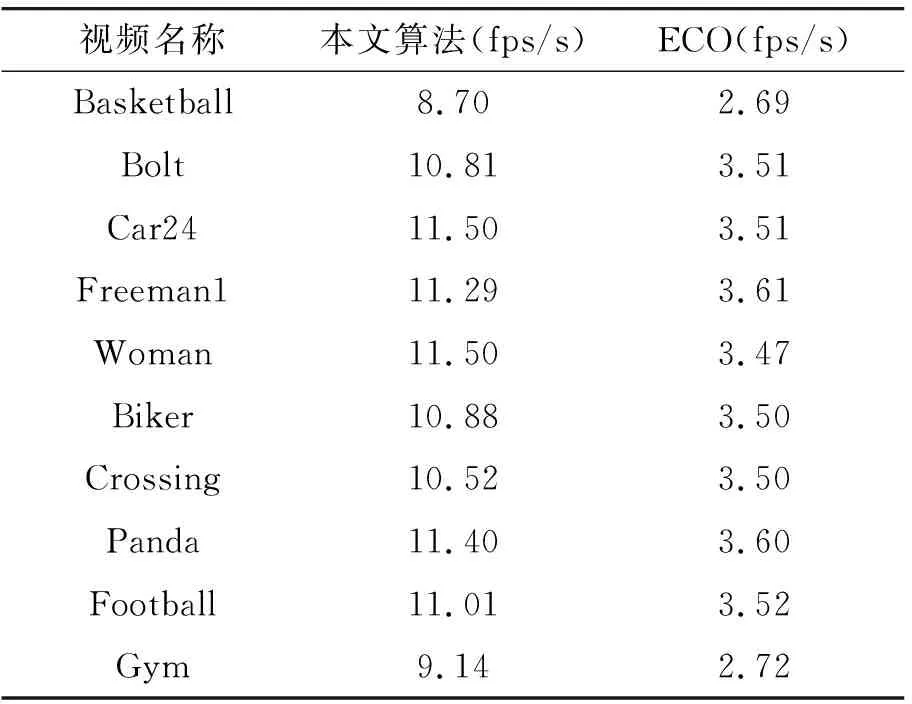
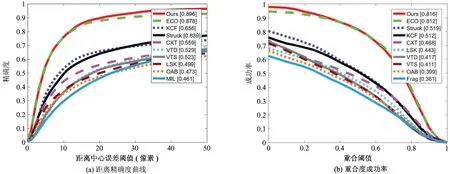
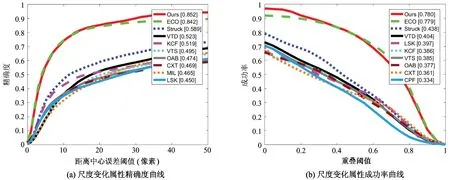
式(4)可以看作2步,首先把插值的特征图乘以PT,得到C维的特征图,然后再和相应的滤波器f进行卷积。因为C 在ECO中,作者应用高斯混合模型来生成训练样本集,目的在于消除冗余和增加训练样本集的多样性。通过样本x和目标输出y的联合概率分布p(x,y),应用高斯混合模型将目标损失函数式(3)进一步完善,用下式来训练滤波器: (5) 式中,L是高斯分组的个数,θl是第l个分组的权重,ul是期望。从式(5)可以发现,高斯期望ul和权重θl直接替换了式(3)中的xj和αj,在L个分组中,每个组内样本高度相似,代表某种特定场景,组与组间差异较大,增加了训练样本的多样性,减小了训练样本集的大小,用式(5)代替式(3)来训练滤波器。 从第1节的介绍可以知道,C-COT和ECO跟踪算法提出一种用于学习连续空间域中的卷积算子的新公式,利用插值模型从预训练好的深度网络中提取出多分辨率特征图。式(1)中利用了双立方插值对提取的特征图进行插值处理。 双立方插值的本质是把图像某个像素点最近的16个像素点权重卷积之和作为新的像素值。双立方插值能得到精确的插补图形,但也计算复杂,所以速度也很慢。在ECO算法中,应用了CNN卷积神经网络提取的特征和人工设计的HOG特征进行融合,CNN卷积神经网络选用的是VGGNet模型。图1是应用VGGNet网络对输入的图片通过不同的卷积层提取的特征图的可视化过程,本文里使用的是16层的VGGNet,应用第3个卷积层(对应图1中的Layer1)提取的特征作为浅层特征和第14个卷积层(对应图1中的Layer5)提取的特征作为深层特征。 图1 VGGNet各层卷积特征图 ECO应用双立方插值把特征图变为连续域来提高分辨率,由于双立方插值计算比较复杂,如果对每层特征图像都进行插值无疑增加了计算的复杂度,从而影响跟踪的速度。对于卷积神经网络提取的特征来说,浅层特征更有利于目标的精确定位,而且浅层特征包含了较复杂的视觉信息,分辨率比较高,深层特征更能表达图像的语义信息,能够提高跟踪器的鲁棒性,但是分辨率会比较低。所以,为了提高跟踪算法的速度,提出了对提取的特征进行分层插值的改进方法,对于分辨率较高的浅层特征不进行插值,对包含较多语义信息的深层特征进行插值。从图1可以看出,随着卷积层的增加,提取的特征越抽象,而且特征图的分辨率也越来越低,对深层特征进行插值来提高其分辨率非常有必要,图2是对深层特征图插值与不插值进行的对比。 图2 插值对比 图2中,左图是提取的未进行插值处理的深层特征图,右图是对左图进行双立方插值处理后的特征图,可以看到直接提取的深层特征图的分辨率非常低,在经过插值处理后,深层特征图的分辨率大大提高,对提高跟踪器的鲁棒性有很大的作用。插值的特征图的公式可以用下式表示: (6) 式(6)是对特征层进行插值的公式,和式(1)一样,bd(t)是插值函数,c2∈{1,…,c2,…,C2}是深层特征第c2个通道,ch∈{1,…,ch,…,Chog}表示HOG特征的第ch个通道,那么卷积算子的公式为 (7) 第1节介绍了样本空间模型的生成方法,利用概率密度分布和高斯混合模型(GMM)把训练样本集的个数分成L个,更新GMM时采用Declercq和Piater提出的在线更新算法。给定一个新样本xj,首先用θm=γ,um=xj初始化一个新的分组m,如果所分的组数超过设定的值,则对GMM进行简化;如果某一分组的权重θl低于预先设置好的阈值,则用新样本替换该组,否则合并2个距离最近的组k和l为一组,合并后的权重和均值由下式得到。 (8) 随着视频帧的不断读取,这种生成训练样本集合的策略会把一些图片从组中剔除掉,用新的一帧代替,这些被替换掉的图片与分组中的图片也存在着很高的相似性,这样直接替换掉会使在训练样本时可能会丢掉一些信息,使训练不充分,对后面进行模型更新时会产生影响。基于上面的分析和研究,本文在样本集合分组上进行了改进,把所有的图片都进行保留,不进行替换,只进行合并。后面的实验结果也验证了改进策略的有效性。 在应用高斯混合模型(GMM)进行训练样本集合分组时,要用到提取的所有特征层的信息进行计算来决定最终当前帧图片的分组情况。由于每种提取的特征在跟踪时对跟踪效果影响不同,简单的等权值融合在一起可能会导致不好的结果,所以应给不同的特征层分配不同的权重来提高分组的效果。不同特征层的权重分配可以用下式来表示: (9) 针对目标运动过程中出现的尺度变化问题,一个理想的尺度估计方法可以精确有效地对目标的大小进行检测提高跟踪准确率。判别尺度空间跟踪(discriminative scale space tracker,DSST)算法是一种精确有效的尺度估计方法,采用1维的相关滤波器进行尺度估计,称为尺度滤波器,它可以将所提出的尺度估计的方法移植到任意算法中去,以下对DSST尺度估计滤波器的原理进行介绍。 尺度滤波器是为适应目标尺度的变化设计的一维滤波器,用来估计目标的尺度变化,算法中尺度评估的原则为 (10) 其中,W和R分别为前一帧目标的宽和高,a为尺度因子,用来对目标大小的控制,S为估计尺度的个数。 设输入样本xj中某一图像块的维度为D,为了得到最佳尺度相关滤波器fscale,最小化代价函数: (11) 其中,*表示卷积,g为期望输出,d表示特征的某一维度,φ为权重系数。将其转换到复频域中采用帕斯瓦尔(Parseval’s formula)定理求解可得: (12) (13) (14) 其中,η是学习率。 设Zj为以上一帧预测的目标位置为中心的图像块,Zj为其经离散傅里叶变换得到的变量,即选定的正样本区域,在新的一帧中可通过求解离散傅里叶变换(DFT): (15) 本文实验硬件环境为Intel Core(TM) i7-8700K 3.70 GHz CPU,内存(RAM)16 GB,算法开发平台Matlab 2016b。为了更好地评估跟踪方法的性能,在实验中,采用OTB100数据集对跟踪算法进行跟踪性能评估。首先对本文算法和ECO算法在跟踪速度上进行了实验对比,从OTB100中选择了10个具有代表性的视频序列对其跟踪速度进行了测试,测试结果如表1所示。从表1中可以看出,本文的方法在跟踪速度上比ECO算法有非常大的提高。这也说明在对提取的特征图进行分层插值的方法是可行的,可以提高跟踪速度。 表1 部分视频跟踪速度对比结果 图3是在OTB100测试集上跟踪算法的成功率曲线图,其中,图3(a)为距离精度曲线图,图3(b)为重合度成功率曲线图。从图3中可以看出,在整体的跟踪效果上,本文算法(Ours)无论是在距离精度上还是在重合度成功率上都比ECO算法要好,而且还超过了其他目前比较流行的算法,比如核相关滤波(KCF)跟踪算法。在精确度上,本文算法(Ours)的结果为89.6%,ECO算法为87.8%,提高了2.05%,在成功率上,本文算法(Ours)的结果为81.6%,ECO算法为81.2%。 本文中使用多尺度滤波器,把目标的尺度估计从ECO算法中的5个改进为DSST算法中提出的33个。图4是针对目标尺度变化进行的测试对比,从图4中可以看到,在OTB100测试集中,有45个视频序列目标的尺度是不断在发生变化的。曲线图的结果显示,本文的算法在面对目标尺度变化时跟踪的精确度为85.2%,成功率为78.0%,ECO算法的跟踪精确度为84.2%,成功率为77.9%,可以看出,本文的算法在精确度和成功率上都比ECO中的尺度估计要好,也表明本文提出的尺度估计方法能较好地应对目标尺度的变化,在一定程度上同时提高了目标的精确度和成功率。 图3 总体成功率 在第2.2节中,对ECO的样本空间生成进行了改进,改进方法有2点:(1)不替换,所有样本都保留分到不同组中;(2)在分组时给不同特征层分配不同的权重。针对不替换策略来生成样本空间模型,在OTB100上做了单独测试,测试结果如表2所示。为了找到最合适的权重分配,在OTB100上也做了大量实验,实验结果如表3所示。 图4 尺度变化曲线 表2中加粗的数据是2种算法中表现最佳的数据,从表2中可以看出,当对生成样本空间采用不替换策略时,本文的算法在快速移动、运动模糊、平面内旋转、低分辨率、遮挡、尺度变化属性下精确度和成功率都超过了ECO算法;在形变和平面外旋转属性下,精确度超过了ECO,成功率略低或持平;在出视野属性下,精确度和ECO持平,成功率高于ECO;但在背景复杂和光照变化下,略低于ECO。但是从整体的效果上看,在成功率上虽然与ECO持平,但是在精确度上好于ECO算法,说明本文提出的不替换策略在一定程度上是能够提升跟踪效果的。 从表3中给CNN提取的浅层和深层特征分配权重不同所得到的结果可以看到,当浅层特征分配的权重为0.8,深层特征权重为0.2时,所得到的结果最好,其中成功率为81.6%,高于ECO,在精确度上为87.6%,略低于ECO。 表2 不替换策略精确度与成功率对比 表3 不同特征层权重分配精确度与成功率对比 在基于深度特征加人工特征与相关滤波相结合ECO目标跟踪算法的基础上,对其进行了3方面的改进。在跟踪速度上,采取对CNN提取的特征层进行分层插值的方法,对其进行了改进,改进后算法的跟踪速度比原来的速度有了很大的提高;在生成样本空间时,为了能保留训练样本更多的信息,保留了所有图片,并且在分组时,考虑到各层权重不同会影响分组情况,即训练样本集,从而影响跟踪效果,所以给浅层和深层特征分配了不同的权重;为了能更好地估计目标的尺度变化,对ECO的尺度估计进行了改进,把DSST提出的尺度估计方法引入到本文中。在OTB100上的实验结果表明,本文算法无论是在跟踪速度上还是在跟踪效果上,都比ECO算法有所提升。1.3 样本空间模型生成
2 改进方法
2.1 CNN特征层分层插值


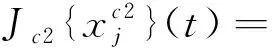
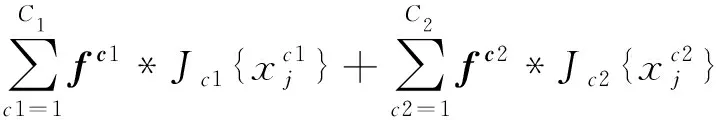
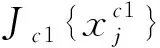
2.2 样本空间分类策略
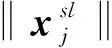
2.3 多尺度估计滤波器

3 实 验
3.1 结果分析
3.2 样本空间分类策略实验


4 结 论

