具有输入约束的移动机器人路径跟踪预测控制①

仇 翔 陈 旭 刘安东 俞 立 周敏龙

(*浙江工业大学信息工程学院 杭州 310023)(** 诺力智能装备股份有限公司 湖州 313100)

0 引 言

随着科技发展，移动机器人因其适应性强、可操作性广等优点，已在军事、工业、科学研究、物流仓储、移动舞台等领域广泛应用。移动机器人路径跟踪控制作为运动控制中的三大基本问题之一，一直备受关注。针对路径跟踪技术的研究，不只适用于移动机器人路径跟踪[1]控制，还涉及无人机路径跟踪[2]、车辆路径规划[3]、自主水下航行器[4]、车床跟踪切削[5]、移动舞台组合[6]等方面，具有重要的理论与实际意义。

近年来，国内外学者提出了多种路径跟踪控制算法，部分研究取得重大成果。其中，Jiang等人[7]基于反演控制方法实现实时反步控制，在初始误差未知的情况下，使系统收敛和稳定。Chen等人[8]提出了一种基于自适应积分滑模控制方法，有效降低干扰对系统的影响，实现系统全局渐近稳定跟踪效果。Rossomando等人[9]提出了在线学习的神经网络算法，该神经网络算法充当传统逆控制器的补偿器，在系统受到动态和运动学变化影响时改善控制性能，有效地对常规逆控制器进行补偿。上述方法解决了初始状态未知、外界干扰等问题，然而，并没有考虑约束问题，本文采用模型预测控制算法在约束条件下实现移动机器人精确的路径跟踪效果。

模型预测控制又称为预测控制，通常包含预测模型、滚动时域优化、反馈优化3个部分，相较于其他的控制方法，预测控制能够及时地校正模型失配以及干扰等引起的不确定性，具有建模方便、系统稳定、扩展性好等优点，在移动机器人路径跟踪控制问题上受到广泛关注。González等人[10]在具有纵向滑动的越野条件下驱动受约束移动机器人，基于模型预测控制算法设计控制律，保证移动机器人路径跟踪的鲁棒性和稳定性。Yu等人[11]将路径跟踪控制问题转化为依赖参数的调节问题，结合模型预测控制方法，选择合适终端惩罚项以及响应的终端约束，实现车载类移动机器人路径跟踪。Li等人[12]通过非完整移动机器人跟踪误差模型以及模型预测控制方法迭代变换为二次规划问题，并使用原始-对偶神经网络获取控制量，解决移动机器人路径跟踪问题。Sun等人[13]基于虚拟结构，采用预测控制方法解决具有输入耦合约束的独轮机器人跟踪控制问题。然而移动机器人在实际运行过程中，存在设定速度与实际速度无法快速匹配的问题。显然，当控制量输入到移动机器人端时，机器人运行时受加速、减速、惯性、电池电量等因素影响，导致移动机器人设定速度与实际速度无法快速匹配的问题。

针对移动机器人路径跟踪过程中存在设定速度与实际速度不匹配的问题，本文提出一种解决速度失配的模型预测控制方法。首先，基于运动学模型建立了移动机器人路径跟踪误差模型，给出了参数化期望路径的更新方程。其次，通过定义与路径参数相关的预测性能指标，并结合状态空间方程推导出预测模型向量描述，得到了具有不等式约束的二次规划优化问题。进而，采用有效集二次规划方法求解具有不等式约束的优化问题获得最优控制量。为了验证本文提出算法的可行性，先通过仿真说明算法的有效性，再搭建移动机器人实验平台，验证算法的有效性。

1 问题描述

移动机器人路径跟踪涉及移动机器人坐标系{B}、虚拟移动机器人坐标系{T}、世界坐标系{W}，如图1所示。

图1 移动机器人路径跟踪坐标系

(1)

(2)

其中，v为机器人实际线速度，ω为机器人实际角速度，vr为虚拟机器人参考线速度，ωr为参考角速度。

根据文献[14]中移动机器人运动学误差模型在平衡点处线性化，可得：

(3)

对式(3)采用零阶保持器进行离散化得：

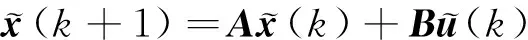
(4)

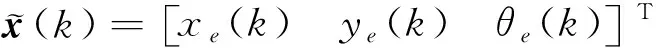
路径跟踪是典型的运动控制问题，与轨迹跟踪的本质区别在于不受时间约束，而是跟踪一个参数化路径[15]。定义参数化期望路径为

P={r(k)∈Rn|r(k)=p(θr(k))}

(5)

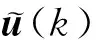
(6)

(7)

由以上分析可知，若r(k)的更新方式只与时间有关，则为轨迹跟踪问题，需要严格的时间管理。而本文为了解决实际速度与设定速度短时间失配问题，选择路径跟踪方式，将控制量误差信号引入到路径更新方式中，使得实际移动机器人的速度与虚拟机器人快速匹配。

本文路径跟踪的目的是使移动机器人实际位姿与虚拟机器人位姿的误差为0，并且虚拟移动机器人的运动路径最终要与期望路径一致。实际移动机器人运动状态逼近虚拟移动机器人运动状态，而虚拟移动机器人的运动状态逼近期望路径相对应的运动状态，如此形成过渡过程。因此，该过程包含有状态误差信息、控制输入误差信息、控制输入误差增益信息，从而可定义预测性能指标函数为

(8)

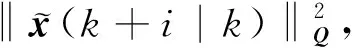
2 模型预测控制

2.1 预测控制

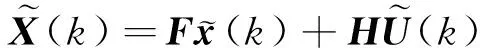
(9)

(10)

对整个系统而言，结合3个惩罚项可得优化目标函数为

s.t. ‖u(k)‖2≤umax(11)

2.2 约束预测控制

将式(9)、(10)代入到式(11)，可得：

其中:

D=HTQH+GT(k)G(k)+R

W=I

I是单位矩阵。从而将优化目标函数式(11)化简为标准的二次规划问题式(12)。

(13)

式(13)的最优解方程为

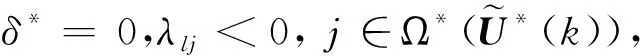
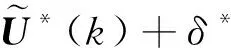
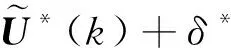
3 仿真结果

为了证明所提算法的有效性，本节给出了数值算例进行仿真验证。基于圆形参考路径，定义其参数化路径如下：

xr=0.8cos(θr)

yr=0.8sin(θr)

(17)

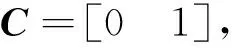
(1) 给出参考机器人初始位姿[xr(1),yr(1),θr(1)]T，实际机器人位姿[x(1),y(1),θ(1)]T，并设置k=0；

(2) 计算各误差向量，并通过有效集方法二次规划求解出k时刻的控制输入偏差量，进而利用预测模型求出k+1时刻状态误差量；

(3) 路径参数θr更新，求解k+1时刻虚拟参考移动机器人状态；

(4) 根据状态误差量以及参考状态解算出k+1时刻实际移动机器人的状态；

(5)k=k+1，返回到步骤(2)。

圆形参考路径跟踪仿真效果如图2所示，其中实线为虚拟参考路径，三角所示为移动机器人初始位姿，虚线为移动机器人实际路径跟踪曲线。尽管在初始状态下，实际移动机器人位姿与参考位姿存在一定偏差，但经过所提预测控制算法多次迭代后实际移动机器人跟踪路径能渐近收敛于圆形参考路径，即位姿状态偏差均能渐近收敛于零，实现跟踪效果。

为了更加直观观察跟踪性能，这里给出了状态误差波形曲线。如图3所示，其由3个误差波形图组成，包括横轴误差波形、纵轴误差波形、角度误差波形，各误差量均能渐近收敛于零，表明实际移动机器人跟踪上了虚拟参考机器人，而虚拟移动机器人路径即圆形参考路径，实现移动机器人的路径跟踪。

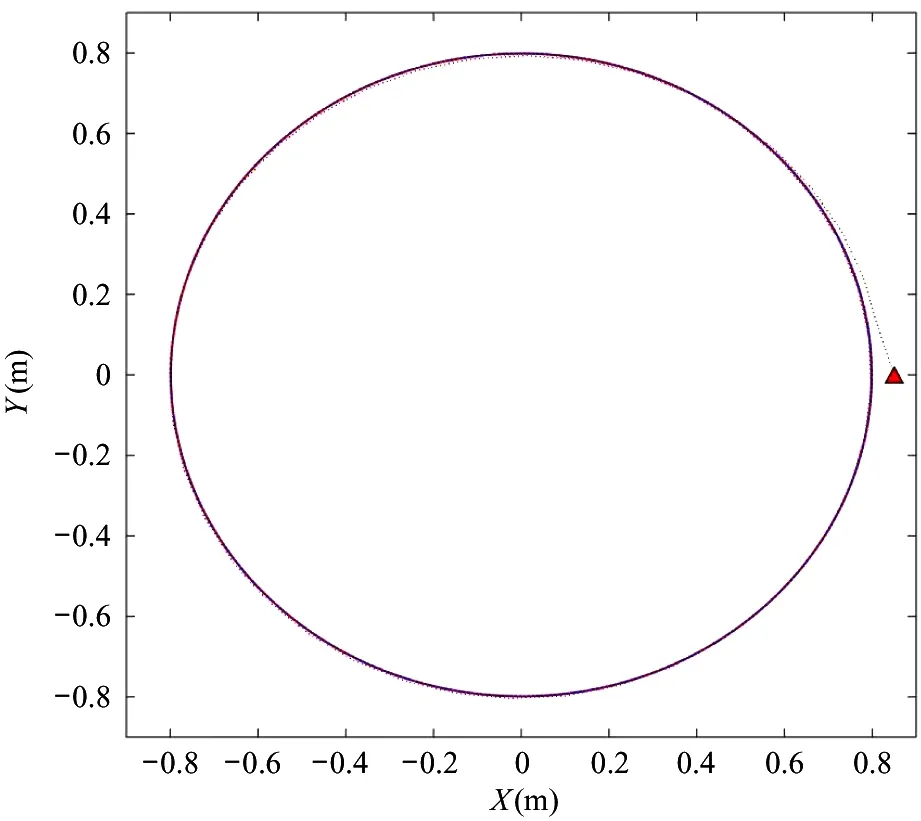
图2 圆形参考路径跟踪

图3 圆形参考路径跟踪误差状态

4 实验结果

4.1 实验平台介绍

第3节通过仿真验证了所提算法的有效性。为了进一步说明该算法的实际意义，本研究搭建了基于Kobuki移动机器人底盘的实验平台。针对Kobuki移动机器人底盘存在设定速度与实际速度无法快速匹配的问题，使用本文所提的预测控制算法设计控制器完成圆形路径跟踪实验，并对不同取值的补偿增益量分析实验结果。

实验设备包括Optitrack位姿定位系统，无线数据传输系统，Kobuki移动机器人驱动控制系统。其中，Optitrack位姿定位系统是利用8个光感摄像头获取Mark点对刚体进行位姿估计，可作为本实验中移动机器人的状态数据反馈。为了实验的可行性，将原本离线的Optitrack位姿定位系统设计成在线模式，无线状态数据反馈系统架构如图4所示，实物图如图5所示。

图4 移动机器人状态反馈通道

图5 Optitrack系统下的移动机器人平台

移动机器人上有4个Mark点，8个摄像头与台式电脑通过有线网络进行数据交互，摄像头采集Mark点数据传给台式电脑求解位姿，Socket通信将位姿信息反馈给机器人端笔记本，从而完成数据状态反馈。

4.2 实验结果与分析

本实验基于实时操作系统，为了直观地得到移动机器人的状态量，基于Qt5.8.0设计上位机，包含3个界面：无线数据接收界面、实时状态及2D机器人路径显示界面、实时波形图显示界面。该上位机开启2个并行线程——主线程和子线程，主线程基于模型预测控制算法给出移动机器人控制量，子线程实时接收Optitrack系统的状态反馈数据并解析。

移动机器人硬件驱动差异性很大，驱动性能与电机控制精度、电池电压稳定程度、轮子摩擦系数、移动机器人本身重量等因素密切相关，这些不可避免的影响导致移动机器人的设定速度与实际运行速度短时间失配问题，使用本文方法可以进行补偿。对于不同驱动设备，λ的取值各不相同。

本文基于移动机器人底盘Kobuki对不同λ取值形成的路径跟踪效果进行分析。首先给出移动机器人数据状态反馈界面，涉及TCP/IP通信协议参数IP地址、端口，接收窗口，数据显示等，数据编码以字母“b”开头，字母“e”结尾，数据本体以空格隔开，反馈界面如图6所示。

当λ=0误差增益补偿时，即控制输入误差量不参与路径更新，不对移动机器人的实际运行状态进行补偿，移动机器人的路径跟踪结果如图7所示，其中实线表示虚拟参考位置，虚线为移动机器人位置，在采样1 000次之后，实线与虚线明显存在较大的角度误差，路径跟踪效果较差。其误差量波形如图8所示，移动机器人的线速度和角速度波动较大，横轴误差与纵轴误差最大值接近300 mm，角度误差最大值接近0.4 rad，总体趋势呈现收敛状态，但收敛速度很慢，误差量很大，无法满足要求。该状态即移动机器人的设定速度与实际的运行速度无法快速匹配，在动态输入控制量时，始终存在误差，从而影响路径跟踪效果，也即本文需要解决的问题。

图6 状态数据反馈界面

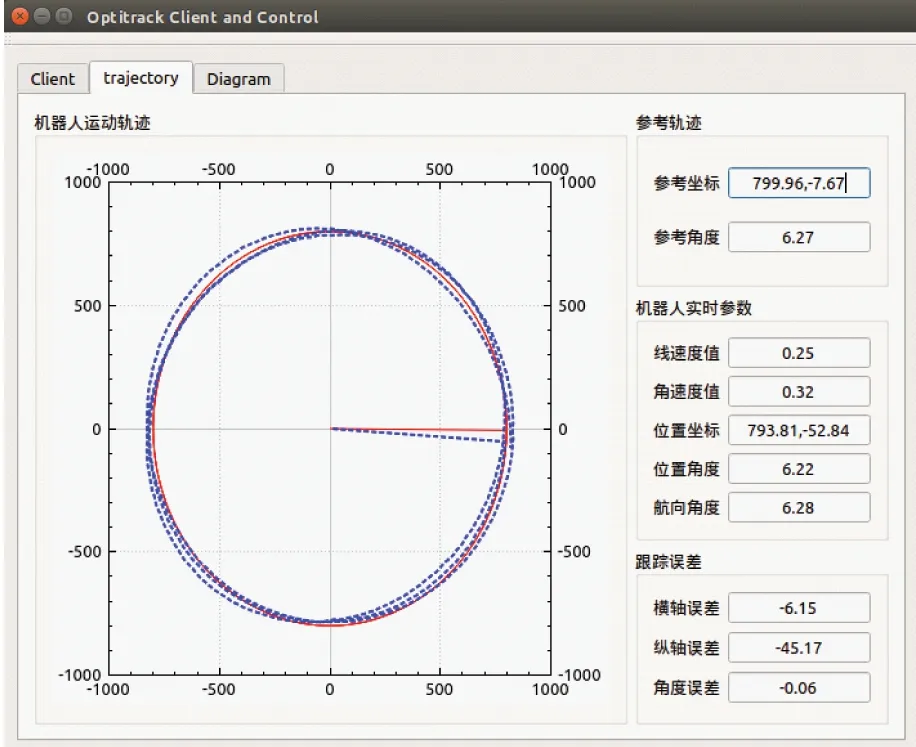
图7 λ=0机器人实时路径及参数

图8 λ=0参数波形图

当λ=0.02的误差增益补偿时，如图9所示，实线代表的虚拟参考位置与虚线代表的实际移动机器人位置重合，路径跟踪轨迹较λ=0时有明显改善，但还存在一定误差。如图10所示，机器人线速度与角速度在长时间内仍存在较大波动，横轴误差最大值接近80 mm，纵轴误差最大值接近100 mm，角度误差最大值接近0.12 rad。引入λ后，移动机器人路径跟踪效果无论是路径轨迹还是误差量均有重大改善，但未趋向完美。

图9 λ=0.02机器人实时路径及参数

图10 λ=0.02参数波形图

当λ=0.05的误差增益补偿时，如图11所示，虚线所示的移动机器人跟踪轨迹与实线所示的虚拟参考路径几乎重合，路径跟踪效果很好。如图12所示，其横轴误差最大值接近40 mm，纵轴误差最大值接近40 mm，角度误差能快速到0附近。在该次实验过程中，移动机器人能很快地达到理想的动态稳定状态，能完美地跟踪上虚拟参考路径，各项误差均近似为0。与λ=0.02相比，λ=0.05使跟踪性能有更好的效果，路径轨迹和误差状态都趋向于完美。

图11 λ=0.05机器人实时路径及参数

当λ=0.3的误差增益补偿时，如图13所示，路径跟踪效果较λ=0.05时变差。如图14所示，其横轴误差达40 mm，纵轴误差达80 mm，角度误差达0.1 rad，较λ=0.05时有所变差。显然，过度补偿导致误差量变大。

综上所述，本文基于模型预测控制算法，结合控制输入偏差量的增益补偿解决移动机器人设定速度与实际速度不能快速匹配的问题。而λ的取值与设备硬件有关，λ取值小不足以补偿，λ取值大又过度补偿。λ取值对跟踪性能的影响如表1所示。

图13 λ=0.3机器人实时路径及参数

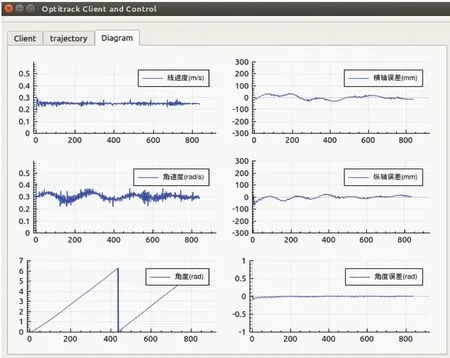
图14 λ=0.3参数波形图

表1 λ取值对跟踪性能的影响

5 结 论

本文针对实际移动机器人存在设定速度与实际速度无法快速匹配的问题，提出了基于模型预测控制的移动机器人路径跟踪方法。首先，基于运动学模型建立了移动机器人路径跟踪误差模型，给出了参数化期望路径的更新方程。其次，通过定义与路径参数相关的预测性能指标，并结合状态空间方程推导出预测模型向量描述，得到了具有不等式约束的二次规划优化问题。进而，采用有效集二次规划方法求解具有不等式约束的优化问题获得最优控制量。通过仿真验证了算法的可行性，并设计移动机器人平台，多次调节λ值，完成圆形路径跟踪实验，跟踪效果理想，充分证明了所提算法的有效性及实际意义。