解析几何（1）

一、填空题

1.（2019年长沙模拟）过点M（-3，5）且在两坐标轴上的截距互为相反数的直线方程为________.

2.直线L1：，L2：x+5=0，则直线L1与L2的夹角为________.

3.直线x-y+5=0被圆x2+y2-2x-4y-4=0所截得的弦长等于________.

4.已知M（1，3），N（5，-2），在x轴上取一点P，使得|PM-PN|最大，则点P的坐标为________.

5.（2018年天津卷）在平面直角坐标系中，经过三点（0，0），（1，1），（2，0）的圆的方程为________.

7.过点P（-4，0）的直线L与圆C：（x-1）2+y2=5相交于A，B两点，若点A恰好是线段PB的中点，则直线L的方程为________.

8.已知点P（t，2t）（t≠0）是圆C：x2+y2=1内一点，直线tx+2ty=m与圆C相切，则直线x+y+m=0与圆C的位置关系是________.

9.在平面直角坐标系xOy中，已知圆C：上存在一点P到直线L：y=2x-6的距离等于，则实数a的值为________.

10.若直线L1：y=x+a和直线L2：y=x+b将圆（x-1）2+（y-2）2=8分成长度相等的四段弧，则a2+b2=________.

二、解答题

11.已知方程x2+y2-2（m+3）x+2（1-4m2）y+16m4+9=0表示一个圆.

（1）求实数m的取值范围；

（2）求该圆的半径的取值范围；

（3）当m变化时，求圆心的轨迹方程.

12.如图，L1，L2是通过某城市开发区中心O的两条南北和东西走向的街道，连接M，N两地之间的铁路线是圆心在L2上的一段圆弧.若点M在点O正北方向，且MO=3km，点N到L1，L2的距离分别为4km和5km.

（1）建立适当的坐标系，求铁路线所在圆弧的方程；

（2）若该城市的某中学拟在点O正东方向选址建分校，考虑环境问题，要求校址到点O的距离大于4km，并且铁路线上任意一点到校址的距离不能少于，求该校址距点O的最近距离（注：校址视为一个点）.

（第12题）

13.（2017年全国卷Ⅲ）在直角坐标系xOy中，曲线y=x2+mx-2与x轴交于A，B两点，点C的坐标为（0，1），当m变化时，解

答下列问题：

（1）能否出现AC⊥BC的情况？说明理由；

（2）证明：过A，B，C三点的圆在y轴上截得的弦长为定值.

14.如图，在平面直角坐标系xOy中，设点M（x0，y0）是椭圆C：上一点，从原点O向圆M：（x-x0）2+（y-y0）2=r2作两条切线，分别与椭圆C交于点P，Q，直线OP，OQ的斜率分别记为k1，k2.

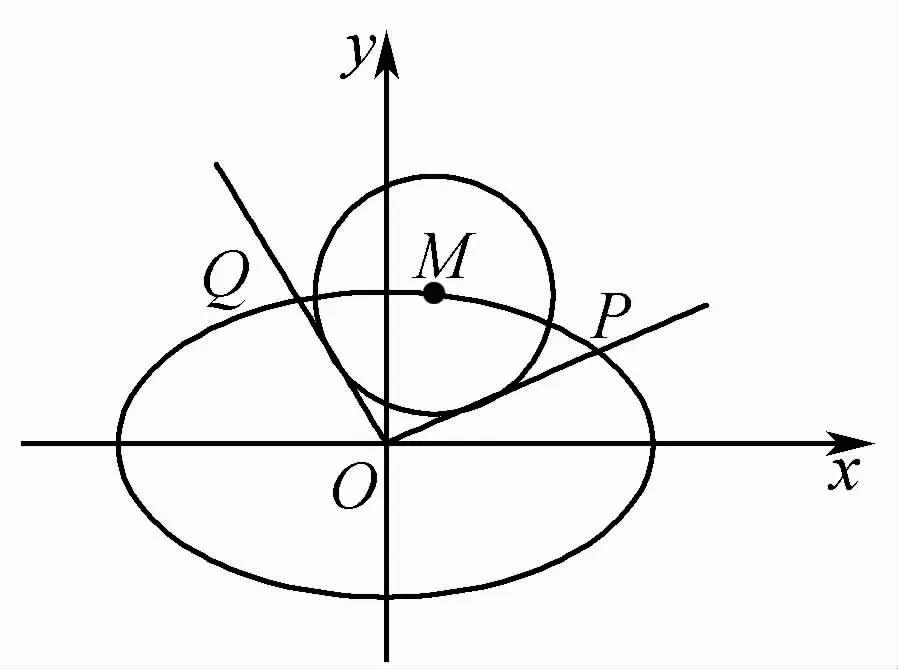
（第14题）

（1）若圆M与x轴相切于椭圆C的右焦点，求圆M的方程；

②求OP·OQ的最大值.