参数值求不出来怎么办

余建国

例 （2016年高考山东文科卷）设f(x)=xlnx-ax2+(2a-1)x,a∈R.

（1）令g(x)=f'(x)，求g(x)的单调区间；

（2）已知f(x)在x=1 处取得极大值，求实数a的取值范围．

解析

（1）由于f'(x)=lnx-2a(x-1)，所以g(x)=lnx-2a(x-1).

①当a≤0时，因为x∈(0,+∞)，所以g'(x)＞0，g(x)在(0,+∞)上单调递增；

②当a＞0时，当时，g'(x)＞0，g(x)在上单调递增；当时，g'(x)＜0，g(x)在上单调递减.

（2）f'(x)=lnx-2a(x-1),f'(1)=0.

①当a≤0时，当x∈(0,1)时，f'(x)＜0；当x∈(1,+∞)时，f'(x)＞0.所以，当x=1时，f(x)取得极小值，不合题意.

敲黑板

观察第(1)小题：函数g(x)含参数，想到了什么？对，分类讨论！

敲黑板

可导函数y=f(x)在点x0处取得极值的充要条件是f'(x0)=0，且在x0左侧与右侧f'(x)的符号不同．也就是说，若已知可导函数y=f(x)在点x0处取得极值，则必有f'(x0)=0，利用这个方程就能求出一个参数的值．

综上，实数a的取值范围是.

反思为什么是2a与1比较大小呢？

这要从课本上的一道习题说起：用函数的单调性证明不等式ex≥1+x，并通过函数图象直观验证.函数y=ex在点(0,1)处的切线方程为y=x+1，除切点外，函数y=ex的图象均在该切线的上方，如图1.

图1

对不等式ex≥x+1 两边取对数，得x≥ln(x+1)，也就是x-1 ≥lnx.此式表明，函数y=lnx在点(1,0)处的切线方程为y=x-1，除切点外，函数y=lnx的图象均在该切线的下方，如图2.

图2

敲黑板

乍看第(2)小题，你是不是想这么简单，利用方程f'(1)=0不就解得参数a的值了？可事实上，无论a取何值，f'(1)=0 恒成立，就是解不出a的值！

其实，高考题第(2)问还不至于这么简单，一定另有乾坤．

“数学是玩概念的”，华罗庚先生说过，解题遇到困难时，我们要学会“退”，退到简单情况，退到概念中去——回到极值的定义．

由f'(1)=0 还不一定说明1 是函数f(x)的极值点，必须结合“两侧异号”；就算是，还要分清是极大值点还是极小值点．所以，我们不能只盯住f'(1)=0，还要看看x=1 的左、右侧f'(x)的符号，即从整体上研究f'(x)（即g(x)）的图象．

敲黑板

由x≥ln(x+1)，得x-1≥lnx，你知道是怎么算出来的吗？对，换元！令t=x+1，则t-1≥lnt，即x-1≥lnx.

因此，如果我们在同一坐标系中画出y1=lnx，y2=2a(x-1)的图象，就会发现：当2a≤0时，它们只有一个交点x=1，且当0 ＜x＜1时，y1＜y2，即f'(x)＜0；当x＞1时，y1＞y2，即f'(x)＞0，所以x=1是f(x)的极小值点，如图3；类似的，当0 ＜2a＜1时，如图4；当2a=1时，如图2；当2a＞1时，如图5.

图3

图4

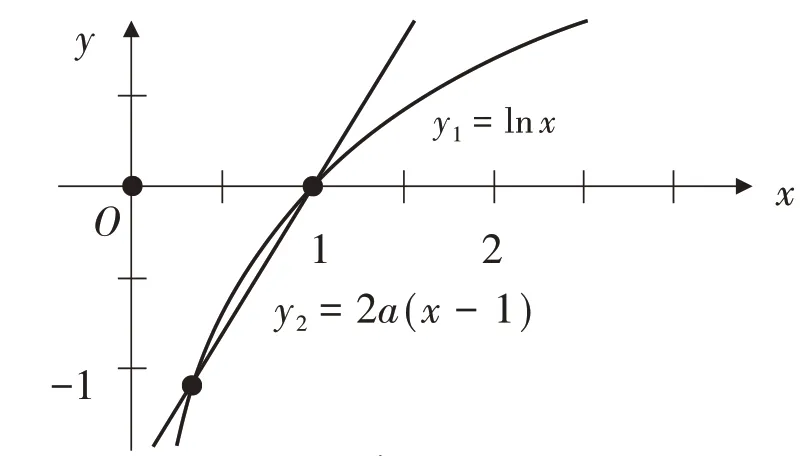
图5

图2 至图5 非常清晰地说明了f'(x)在x=1 处左、右侧的符号情况.

高考题并不神秘，它来自课本，但高于课本，所以同学们一定要理解透数学概念，看课本!看课本!看课本!

敲黑板

图形不能代替证明，必须像前面的解答过程那样去说理，但图可以引导我们怎样说理．

真题练

1.(2018年高考北京文科卷)设函数f(x)=[ax2-(3a+1)x+3a+2]ex．

(1)略；

(2)若f(x)在x=1处取得极小值，求a的取值范围．

2.(2018年高考北京理科卷)设函数f(x)=[ax2-(4a+1)x+4a+3]ex．

(1)略；

(2)若f(x)在x=2处取得极小值，求a的取值范围．

3.(2018年高考新课标Ⅲ理科卷)已知函数f(x)=(2+x+ax2)ln(1+x)-2x．

(1)略；

(2)若x=0 是f(x)的极大值点，求a．