马科维茨均值-方差理论在能源期货投资组合优化中的运用

王一凡

(湖南师范大学商学院，湖南 长沙 410012)

0 引 言

能源是现代社会发展的血液，经济建设、社会生活与文化发展都与能源息息相关。能源的使用渗透在社会生活的方方面面，如交通运输业、建筑业、制造业、旅游业等。而能源交易一般集中于期货交易，如美国的NYMEX原油期货。世界著名的能源期货交易所有纽约期货交易所、伦敦国际石油交易所等。由于期货交易所的存在，投资者也可进入能源市场进行投资获利，同时，投资者的进入与杠杆交易的特点导致了大量的投机行为并且被杠杆进一步放大，导致能源期货交易的波动巨大，稍有不慎便面临巨大的风险。

2020年4月21日，五月到期的WTI原油期货跌至负数，空方的投机行为使原油期货价格跌落至负数，为多方带来了巨大损失。如果运用马科维茨的投资组合理论对原油期货产品进行分散化投资，利用历史数据计算出最佳投资策略，可以使投资者有效规避这种投机行为带来的非系统性风险，实现稳定收益。

马科维茨于1952年提出均值-方差组合理论。他认为，大量的投资组合可以完全规避非系统性风险。该理论被提出后，得到了学者广泛应用与研究。随着时间的推移，许多学者对该理论的有效性进行了研究，并不断完善该理论。肖赵华[1]系统地论述了自马科维茨均值-方差理论开始的资产配置理论。文献[2-4]对马科维茨均值-方差理论的算法进行了优化。文献[5-13]通过放宽限制条件，对马科维茨均值-方差理论体系进行了优化。文献[14-18]以现实数据为依据，对马科维茨均值-方差理论进行了实证检验。文献[19-22]对马科维茨均值-方差模型进行了拓展，并通过实证检验验证其拓展模型的有效性。

综上所述，学者们在该理论无论是实证还是理论方面都进行了充分的研究。然而，将马科维茨均值-方差理论应用于期货投资的研究并不多。同时，少量资产进行组合的有效性暂且未知，但大量的资产进行组合后，计算量巨大，使实践中个人投资者很难做到最佳投资比率的计算。

因此，本文选取4种能源期货资产，通过实证验证其投资组合的有效性。这说明，少量的能源期货资产进行组合后，可以有效规避非系统性风险，并提供了动态投资组合策略。

1 马科维茨均值-方差理论模型

1.1 最佳投资比率计算

马科维茨均值-方差理论是经典的投资组合理论，它验证了投资组合可以有效地分散系统性风险。刘科弟[23]系统地论述了经典理论模型，本文以其作为理论基础，在进行实际投资时，模型如下：

选择纽约商业交易所的天然气1号期货合约、取暖油1号期货合约、RBOB常规油1号期货合约以及OK原油1号期货合约进行风险分散。为了简化计算，本文规定以上4种合约分别称为资产x1、x2、x3、x4，其权重分别为ω1、ω2、ω3、ω4。同时，令X=(x1,x2,x3,x4)T，W=(ω1,ω2,ω3,ω4)T，且资产xi的收益率为ri，期望收益率为E(ri)，资产之间的协方差为σij，i=j时，即为资产本身的波动率。由于是期货合约，因此允许卖空，并且假设不考虑保证金账户收益。

规定资产组合为P，收益率为Rp，波动率为σp，则有以下等式：

P=WTX

(1)

(2)

(3)

(4)

(5)

根据以上等式，可以运用拉格朗日乘子法得到资产组合P在定期望收益率的情况下的最小方差，从而得到预期收益率与最小方差的关系，最终得到资产组合P的有效边界，计算过程如下：

引入拉格朗日乘子α,β，记E=(E(R1),…,E(R4))T,∑=(σij)4×4,1=(1,1,1,1)T。构造拉格朗日等式：

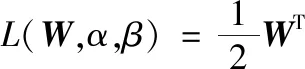
对W、α、β求导，得到：

解该方程组，令A=ET∑-1E,B=1T∑-1E,C=1T∑-11,D=AC-B2，有：

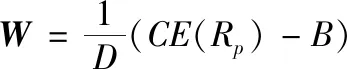
从而可以计算出给定资产组合P的预期收益率E(Rp)下的最小波动率为：

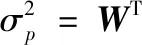
从而得到σp与E(Rp)的关系，即：

因此，资产组合P的有效边界为双曲线M的右半支中处于第一象限的部分，即σp>0,E(Rp)<0的部分。资产组合P的最佳投资比例所对应的收益率与波动率即为有效边界上使夏普比率最高的收益率与波动率的收益率和波动率。该点为使该点与无风险收益率形成的直线与双曲线相切的点(σp,Rp)。

为了简化运算，令σp=x,E(Rp)=y=f(x),x>0,y>0，则有：

设双曲线M上有一点(x0,y0)，其与(0,Rf)形成的直线与双曲线相切，双曲线M等式两边同时对x0求导，可得：

1.2 检验方法

为验证最佳投资比率W的有效性，本文使用历史数据模拟的方法进行检验。即选取[n，n+252]天作为模拟区间，取[n+1，n+253]天作为检验区间，n滚动k次，得到k个样本。即，投资者持有资产的时间长度为一个交易年度。在假设第n+253天价格不确定的情况下，DeMiguel等人[24]证明，比起绝大多数其他投资策略，等权重投资是最为有效、稳健的投资策略。因此，在第[n+1，n+253]天的检验区间中，运用等权重投资进行检验。

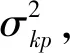
2 实证部分

2.1 数据选择

首先，关于k的选择，本文选择了k=251，即滚动一个交易年度减一天。其次，由于收益率的数据需要2个交易日价格数据计算，本文选取了最近505个交易日期货价格数据，即2个交易年度加一天的交易数据，如图1～图4所示。

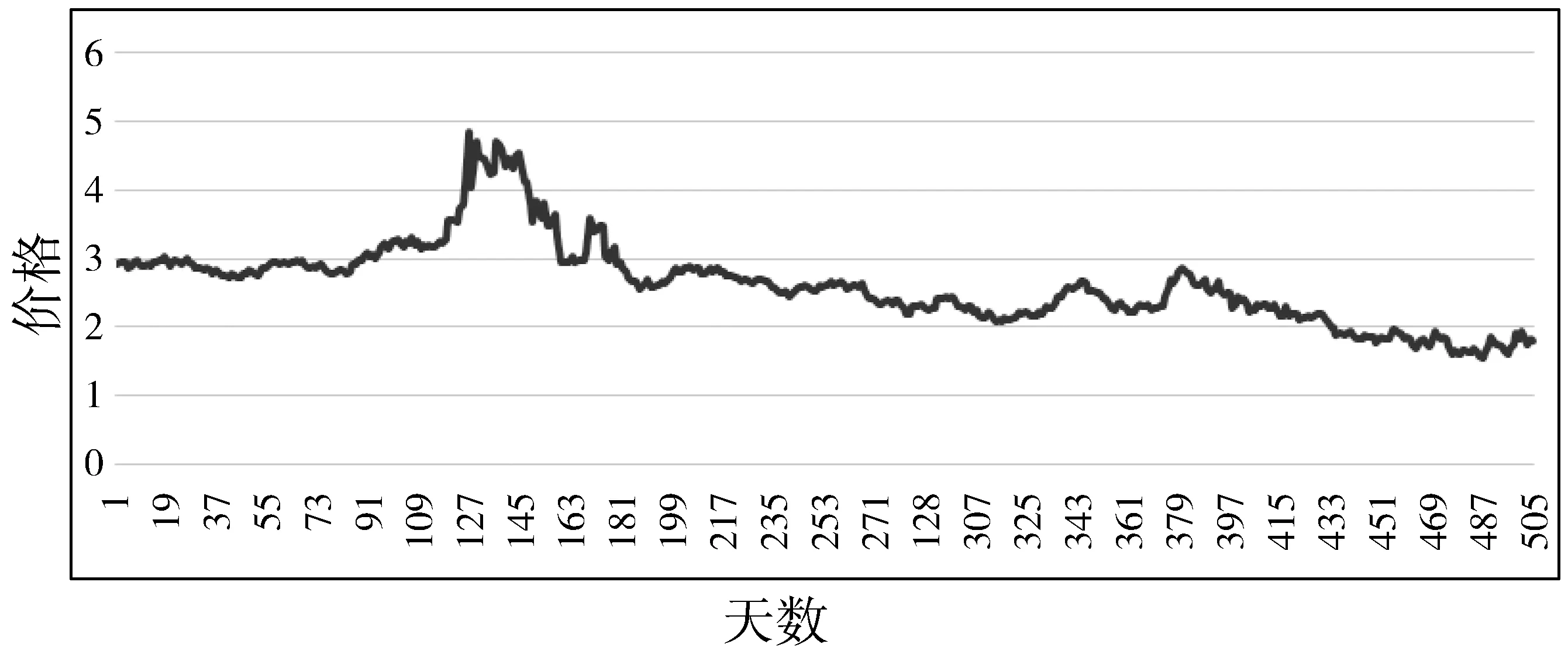
图1 2018-05-23日—2020-04-28日天然气1号期货合约交易趋势图

图2 2018-04-26日—2020-04-28日取暖油1号期货合约交易趋势图

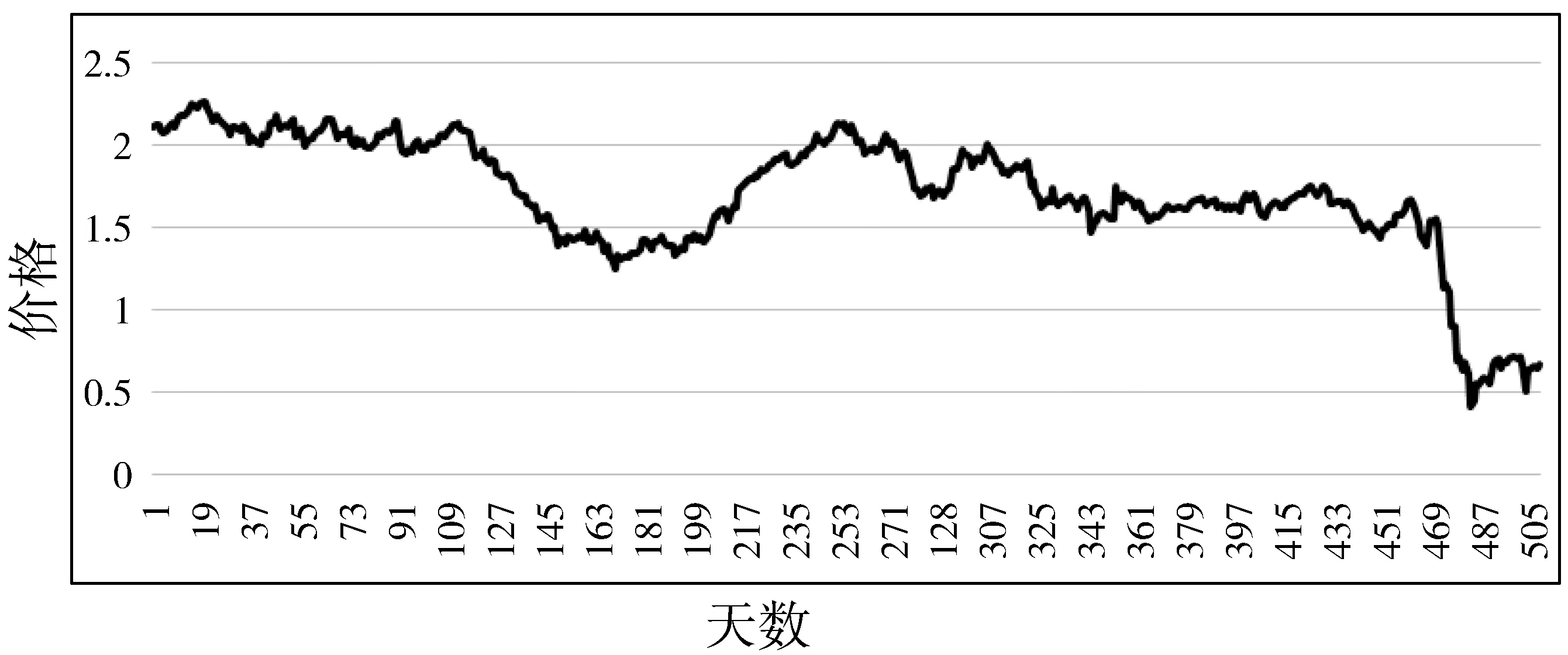
图3 2018-05-07日—2020-04-28日RBOB常规油1号期货合约交易趋势图

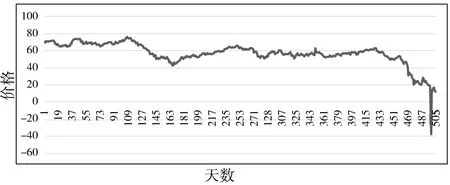
图4 2018-04-27日—2020-04-28日OK原油1号期货合约交易趋势图

从图中可以直观看出，最近2个交易年度内，4种资产的交易价格主要由空方主导，价格趋势不断下行。因此，本文认为投资者主要进行空头交易。但在进行投资组合时，也有投资权重为负的可能，此时，投资者要作为多头交易，因此，排除多头交易的可能。但是，期望收益率是以空头为标准计算，其估计为：

在第[n+k，n+k+252]日中，每一日的收益率如下：

从而可以计算出4种资产在第k个样本中形成的协方差矩阵∑k。

同时，在无风险收益率的选取上，本文选取了美国一年期国库券的2019-06-03日—2020-06-01日的收益率的均值作为无风险收益率的期望收益率，数据如图5所示。

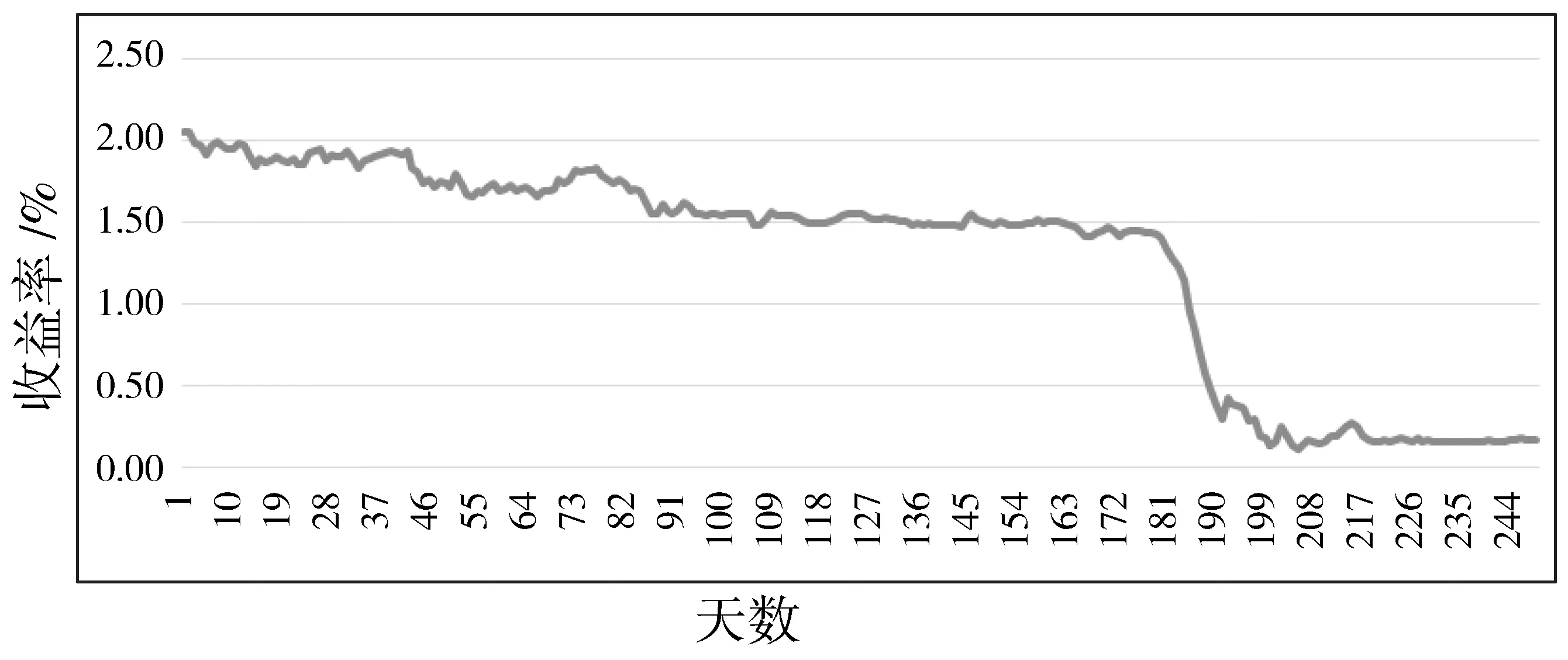
图5 一年期美国国库券每日年化收益率

计算得无风险收益率Rf=1.28%。

2.2 数据计算

通过以上数据，可以求得第k个[n,n+252]日的最佳投资比例Wk，共有252个数据。结果如图6～图9所示。

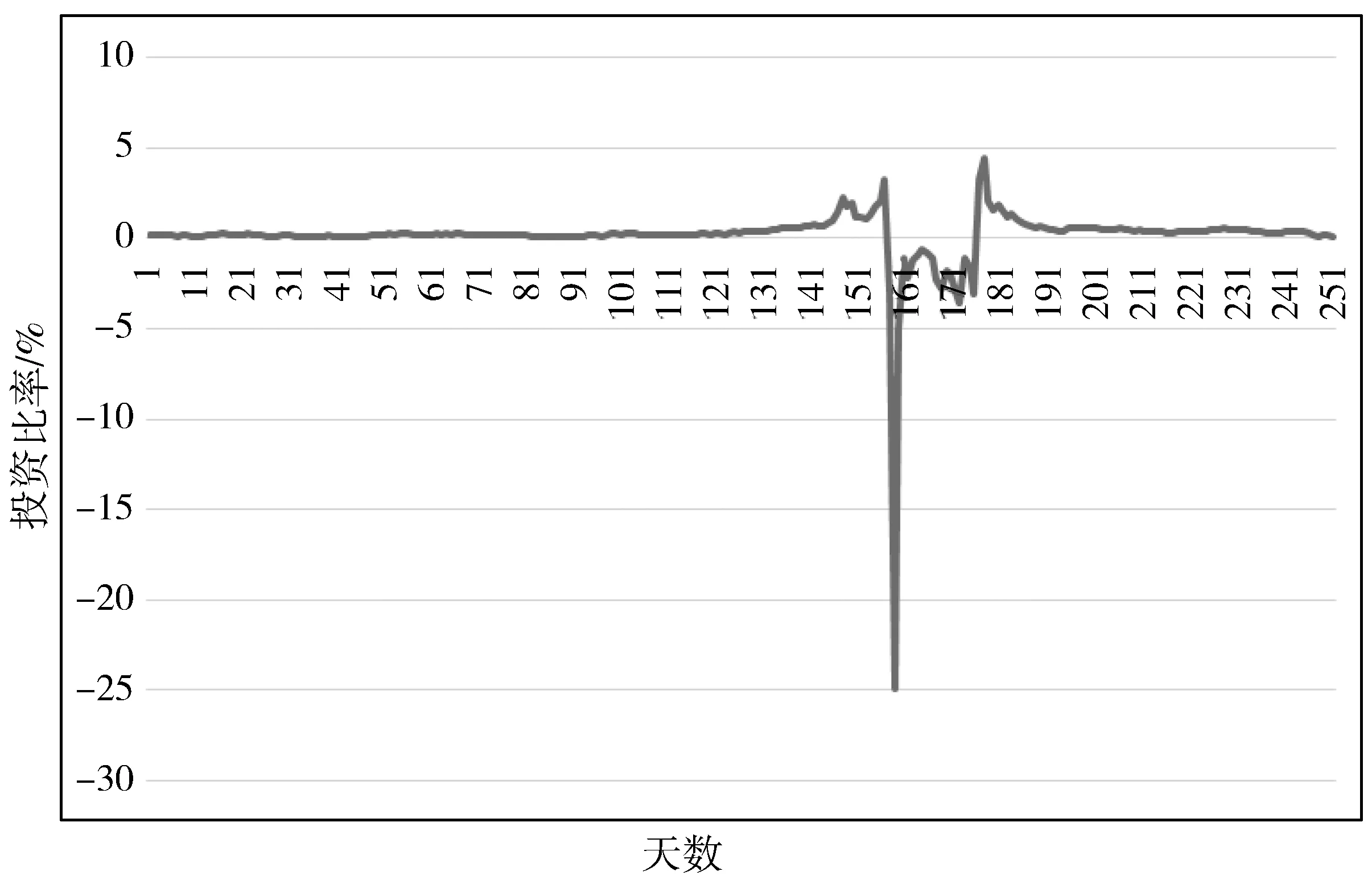
图6 天然气1号期货合约最佳投资比率

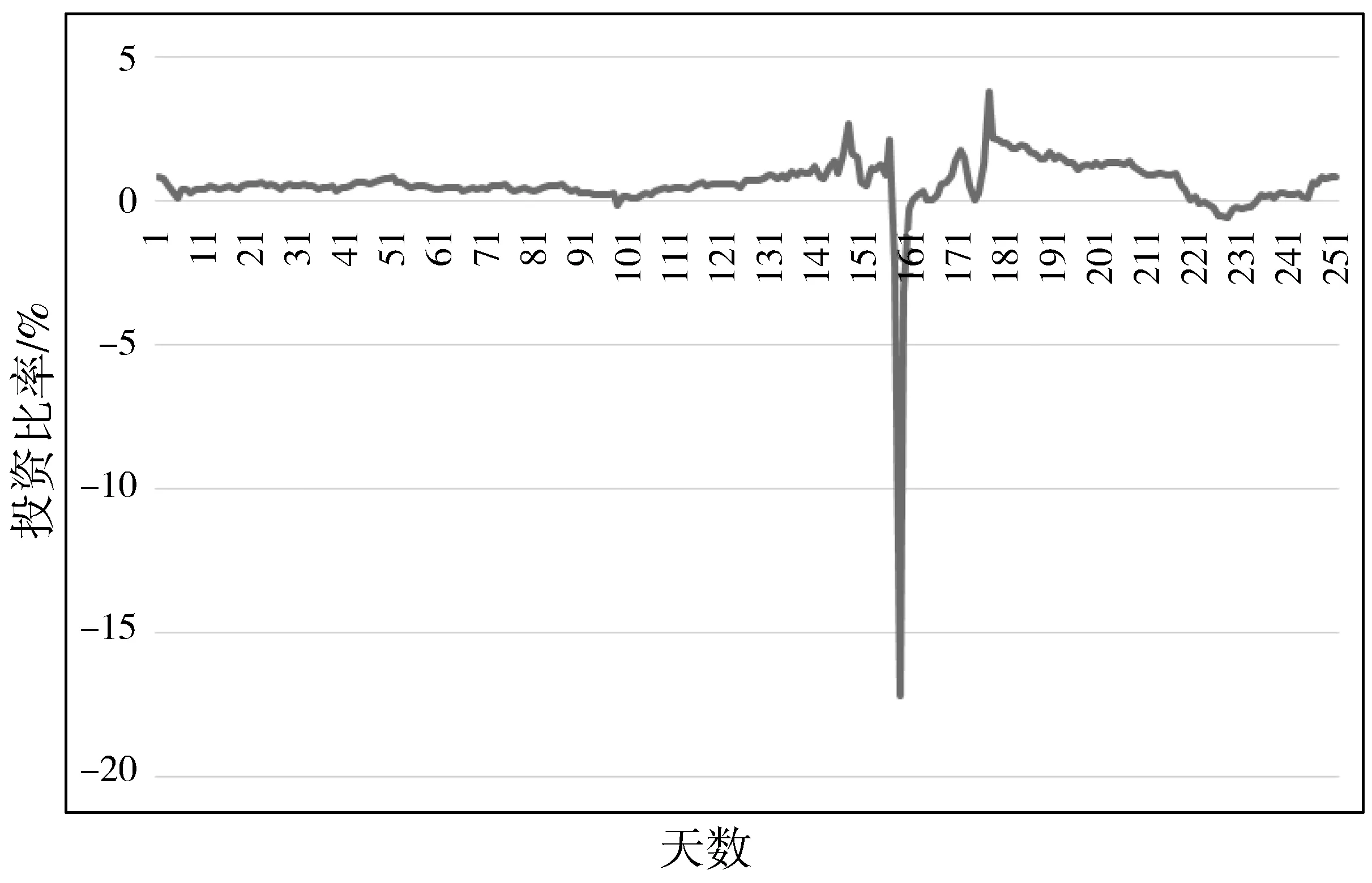
图7 取暖油1号期货合约最佳投资比率

图8 RBOB常规油1号期货合约最佳投资比率

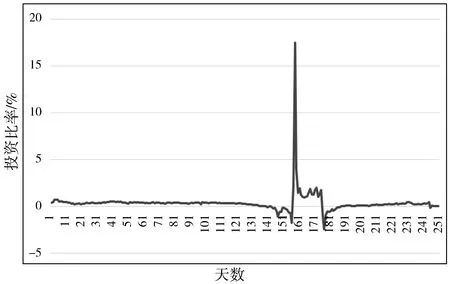
图9 OK原油1号期货合约最佳投资比率

从图中可以直观看出，只有极少一段时间，最优资产组合比率的分配发生了较大波动。因此，投资者可以更接近于静态持有投资组合，可以为投资者节约时间成本。为进行进一步分析，对4种比率进行ADF检验。检验结果显示，4种比率均为平稳序列。因此，进一步证实该资产比率的有效性。

2.3 结果检验

将该数据代入第k个[n+1,n+252]日后，可得该投资比率投资于检验区间的夏普比率Sharpratiok+1，将其与等权重投资所得的夏普比率Sharpratiok进行比较，比较结果如图10所示。

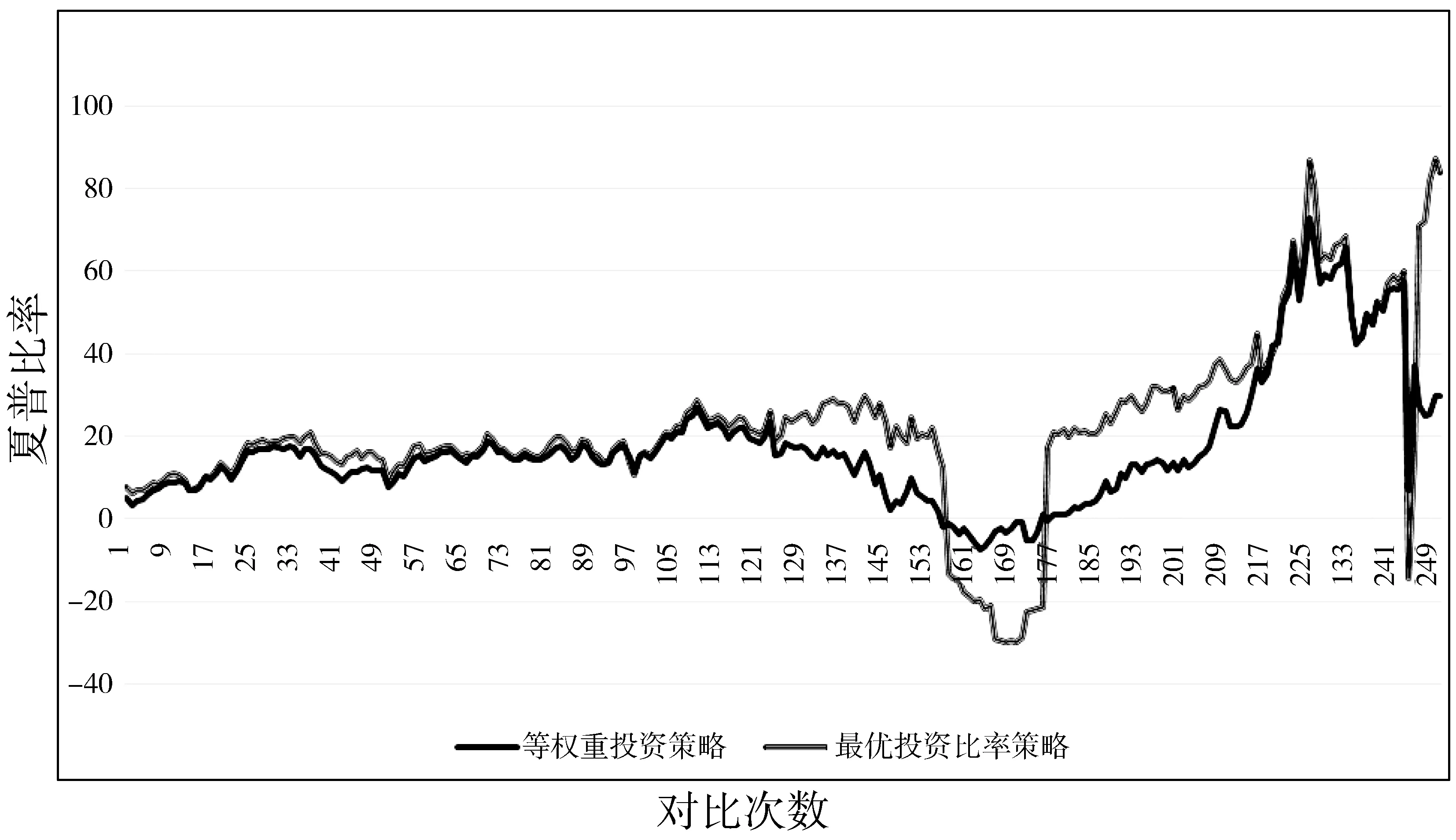
图10 夏普比率对比图

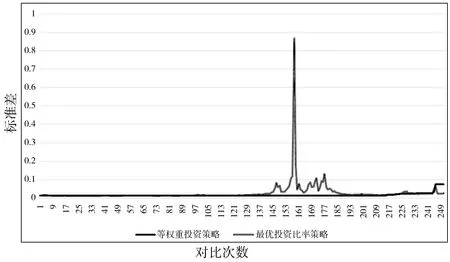
图11 标准差对比图

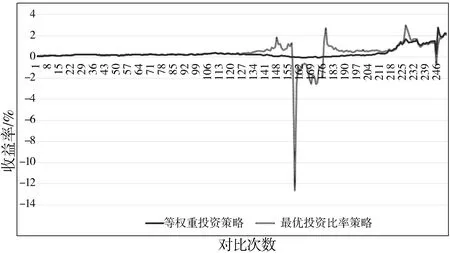
图12 期望收益率对比图

从图中可以看出，仅有极少一部分最优投资比率策略恶化等权重投资策略的风险，且绝大部分情况下等权重投资策略与最佳投资比率策略的风险相差无几。因此，最佳投资比率策略降低风险的效果并没有优于等权重风险，仅与等权重投资策略接近。

可以看出，最佳投资比率策略在后半段中绝大部分明显优于等权重投资策略，其中有一小段明显劣于等权重投资策略。因此，最佳投资策略比率在期望收益率上优于等权重投资策略。

综上所述，最佳投资比率策略部分优化了等权重投资策略，并且绝大部分策略至少没有劣于等权重投资策略。

3 结束语

本文依据马科维茨均值-方差理论，根据第k个[n,n+252]日的期货交易数据，构造了252个最佳投资比率。同时，以第k个[n+1,n+253]日的数据作为最佳投资比率的检验区间。结果显示，最佳投资组合比率中各资产组合比率的变化是平稳的。并且在绝大部分情况下，最佳投资比率组合的夏普比率优于等权重投资比率。同时，经过检验后，期望收益率显著优于等权重投资比率，而方差并没有得到显著优化。因此，利用历史数据进行最佳投资比率模拟，并将该比率应用于未来投资时，相比于绝大部分投资组合的等权重投资，该投资组合显著优化了期望收益率，并保持了与等权重投资相近的风险。因此，即使对于非大量的投资组合，进行投资组合优化依然可以有效分散非系统性风险，实现相对较好的收益。同时，最佳投资组合比率在滚动的过程中，表现出良好的平稳性，等权重投资可进行静态调整的优势被减小，进一步体现了最佳投资组合的有效性。

根据上述结论，可以得出以下建议：

1)期货投资具有高杠杆性，无论是收益还是损失都是巨大的。投资者应善用投资组合，规避可能出现的巨大损失。

2)即使是少量的投资组合，资产组合的夏普比率也得到了显著提升。因此，少量的投资组合依然可以规避非系统性风险，实现较为安全、稳定的收益。

3)相比于静态的等权重投资，不断调整最优投资组合的动态权重投资可以得到更好的收益，并稳定风险。然而，随着资产数量的增加，最优投资比率的计算量也在不断增加，调整最优投资比率也不断复杂。因此，对于个人投资者而言，更好的方案是选择适当的资产数量，而不是选择过高的资产数量，追求近乎于0的非系统性风险。

4)在对该组合进行投资时，最优投资比率的波动并不大。因此，持有该资产组合可以进行少量的动态调整，投资者无需花费过多精力调整投资比率，节省投资者的时间成本。