基于组合支持向量回归的排污企业生产识别

(国网四川省电力公司电力科学研究院，四川 成都 610041)

0 引 言

信息技术和互联网技术的快速发展使得大数据分析和人工智能等新技术应用应运而生，在建设电力物联网的背景下，大数据和人工智能新技术与能源行业相结合引发了越来越多研究人员的关注[1]。电力大数据平台在全面管控电网营销服务和企业安全生产等方面获得显著成效[2-3]。一种应用电网用电信息采集系统数据以实现城市大气污染排放在线管控的方法被提出。该方法基于大数据手段，将电网企业用电信息采集系统电量与环保管控数据进行批量化关联分析，无需新增硬件设备，实现了城市企业大范围在线监管，其中，排污企业对于环保措施的响应程度评判是电力数据在环保应用的一个重要功能。

支持向量机(support vector machine，SVM)是在分类、回归和其他学习任务方面广受欢迎的一种机器学习方法，在计算机视觉、自然语言处理、神经成像、生物信息学等领域已有成功的应用[4]。支持向量机一般分为3类：支持向量分类(support vector classification,SVC)、支持向量回归(support vector regression,SVR)和一类支持向量机(one-class support vector machine ,1-SVM)[5]。其中：根据分类特征，支持向量分类可分为两值分类和多值分类；支持向量回归用于处理数据回归问题；支持向量机还可实现一种特殊的一类分类问题，有学者将其称为一类支持向量机(one-class support vector machine,1-SVM)，在实际中通常应用于异常值检测[6]。

下面研究以企业用电和纳税信息为特征的排污企业生产状态识别方法，考虑到实际输入特征异常和部分缺失的情况，采用回归分析解决数据异常和部分缺失的问题，提高了分析结果的鲁棒性；通过网格搜索选择多个支持向量回归组合模型来识别污染企业生产状况，增加了模型的泛化能力，提高了分类精度。

1 支持向量机数学模型

从模式分类中可分离模式的情况下了解支持向量机是如何工作的可能是最容易的。给定可线性或非线性分离的训练样本，支持向量机通过非线性核函数映射，生成一个超平面作为决策曲面，使得正例和反例之间的隔离边缘被最大化。

考虑训练样本{(xi,yi),i=1,2,3...N}，xi为输入模式的第i个样例，yi为对应的期望响应，用于分离的超平面形式的决策曲面方程为

wTx+b=0

(1)

式中：x为输入向量；w为权值向量；b为偏置。对于一个给定的权值向量w和偏置b，支持向量机的目标就是找到一个特殊的超平面，这个超平面的分离边缘最大。支持向量机是一个二次规划问题，数学推导如下。

当样本中yi=+1和yi=-1代表的两类模式是线性可分时，式(1)可以为

wTxi+b≥0 当yi=+1
wTxi+b≤0 当yi=-1

(2)

考虑使式(2)等号成立的那些点，也就是距离超平面最近的两类点，只要成比例地调整w和b的值就能保证这两类点的存在，且对分类结果没有任何影响。设2个超曲面为H1、H2。

H1:wTx+b=1
H2:wTx+b=-1

(3)

对于非线性问题，可以通过非线性变换转化为高维空间的线性问题。因此，对于非线性分类，首先，采用一个映射φ将数据映射到一个高维空间。此时，在高维特征空间中就可对输入数据进行线性分类，映射回原空间后就成了输入数据的非线性分类。支持向量机采用了一个核函数K(x,y)代替高维空间的内积运算，避免高维空间的复杂运算。为使得所有样本都能被分离超平面正确分类，增加模型的鲁棒性，可采用松弛变量解决这个问题，因此优化问题为

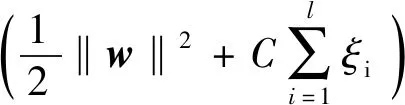
(4)

式中：w是权值向量；C为惩罚因子；ξi为松弛变量。

约束为

wTΦ(xi)+b≥1-ξii=1,……,l
ξi≥0i=1,……,l

(5)

式中：Φ(xi)为核函数。

2 排污企业生产识别

2.1 排污企业生产识别整体流程

基于组合支持向量回归的排污企业生产识别的输入数据为企业的用电量和税收值，与企业生产状态有强相关性。对输入数据进行归一化处理可直观迅速判断企业的基本运行情况，同时大量简化了计算。规则化后的输入数据存在负值或缺失的情况，这是异常的输入数据。通过对企业用电量和税收值的历史回归分析，可校正负值的输入数据，预测缺失的输入数据，提高了分析结果的鲁棒性。

将输入数据分为3部分：训练数据、验证数据和测试数据。输入数据用来训练支持向量回归的超参数，不同的超参数对应一个支持向量回归模型。通过网格搜索可以确定多个支持向量回归模型，验证数据用来筛选已确定的支持向量回归模型，得到最优的支持向量回归模型集用于组合回归判断，可提高单一模型的精度。最后，将最优的支持向量回归模型集来测试历史数据。排污企业生产识别整体流程如图1所示。

2.2 排污企业数据来源

排污企业的主要数据有企业类型、企业注册地、企业纳税、企业用电等，取自于不同的机构。其中，企业类型和企业注册地来自四川省工商局，企业纳税历史数据来自于四川省税务局，企业用电历史数据来自国网四川省电力公司用电信息采集系统和营销系统。将历史数据分为3部分：训练数集、验证数集和测试数集。其中，训练数据用来确定模型的参数；验证数据用来做模型验证，选定预测误差小的超参数组合，提高总模型的精度；最后，测试数据用来做模型测试及分析结果。

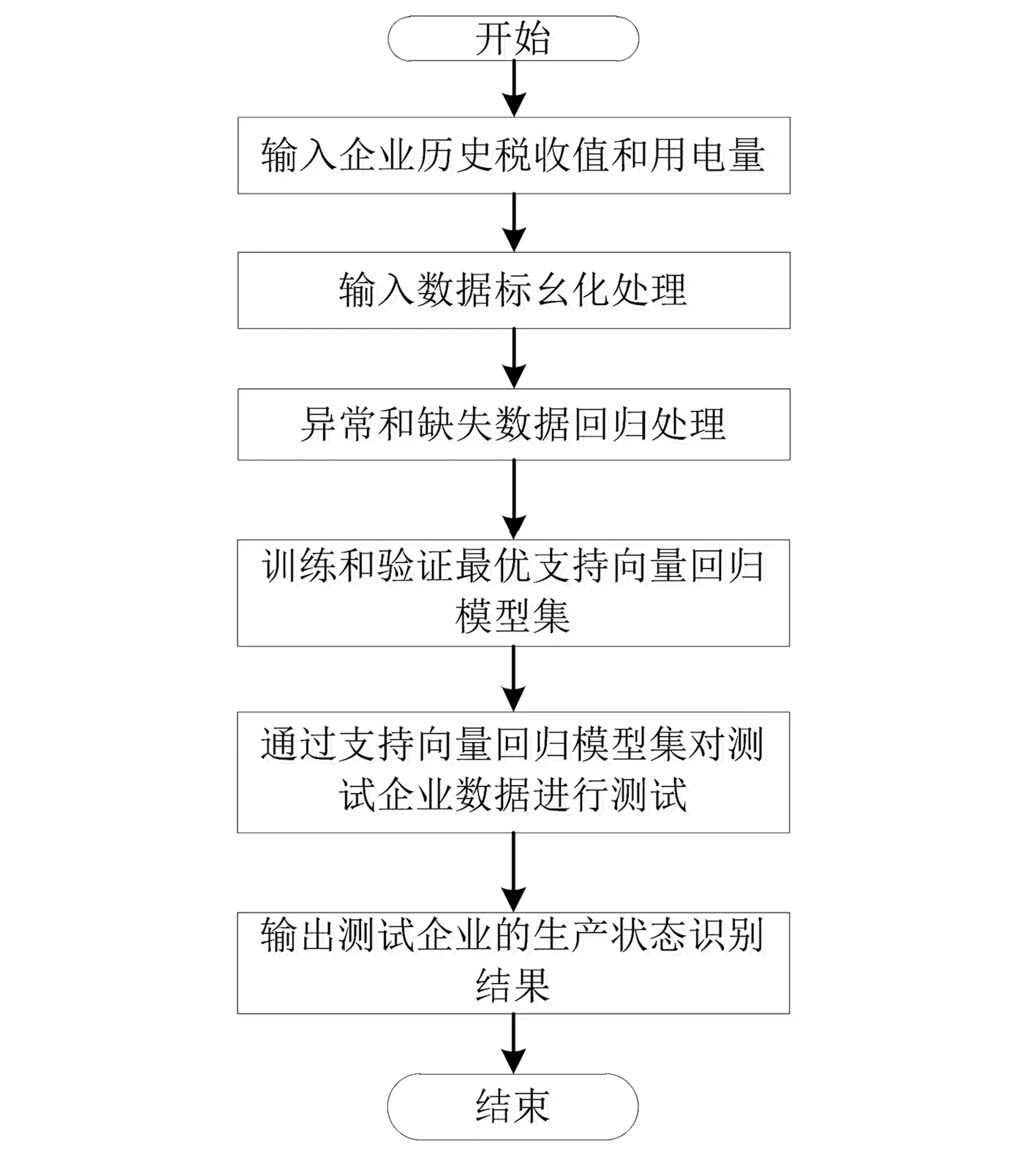
图1 排污企业生产识别总体流程

2.3 输入特征选择与正则化

支持向量机的输入特征选择为企业用电量和纳税值。这两个特征与企业生产密切相关，输出数据为企业开工判据。

输入数据为企业用电量和纳税值，输出数据为企业开工判据，其中，输入数据的幅值远远大于输出数据的幅值。为了降低运算难度，输入数据的大小被规则化，企业用电量被企业配电变压器容量整除，纳税值被最大纳税值整除，则企业用电量和纳税值规则化后的范围均为[0,1]。

(6)

实际情况中存在输入特征值为负或者缺失的异常情况，为处理这种异常值情况，通过历史数据回归建立起企业用电量和纳税值的关系，如图2所示。

图2给出了企业历史的税收值和用电量，存在异常与缺失，图3对缺失与异常做了标记，通过回归分析，可对异常输入特征进行修正，并填补缺失的特征，如图4所示。

图2 企业历史输入特征(存在特征异常与缺失)

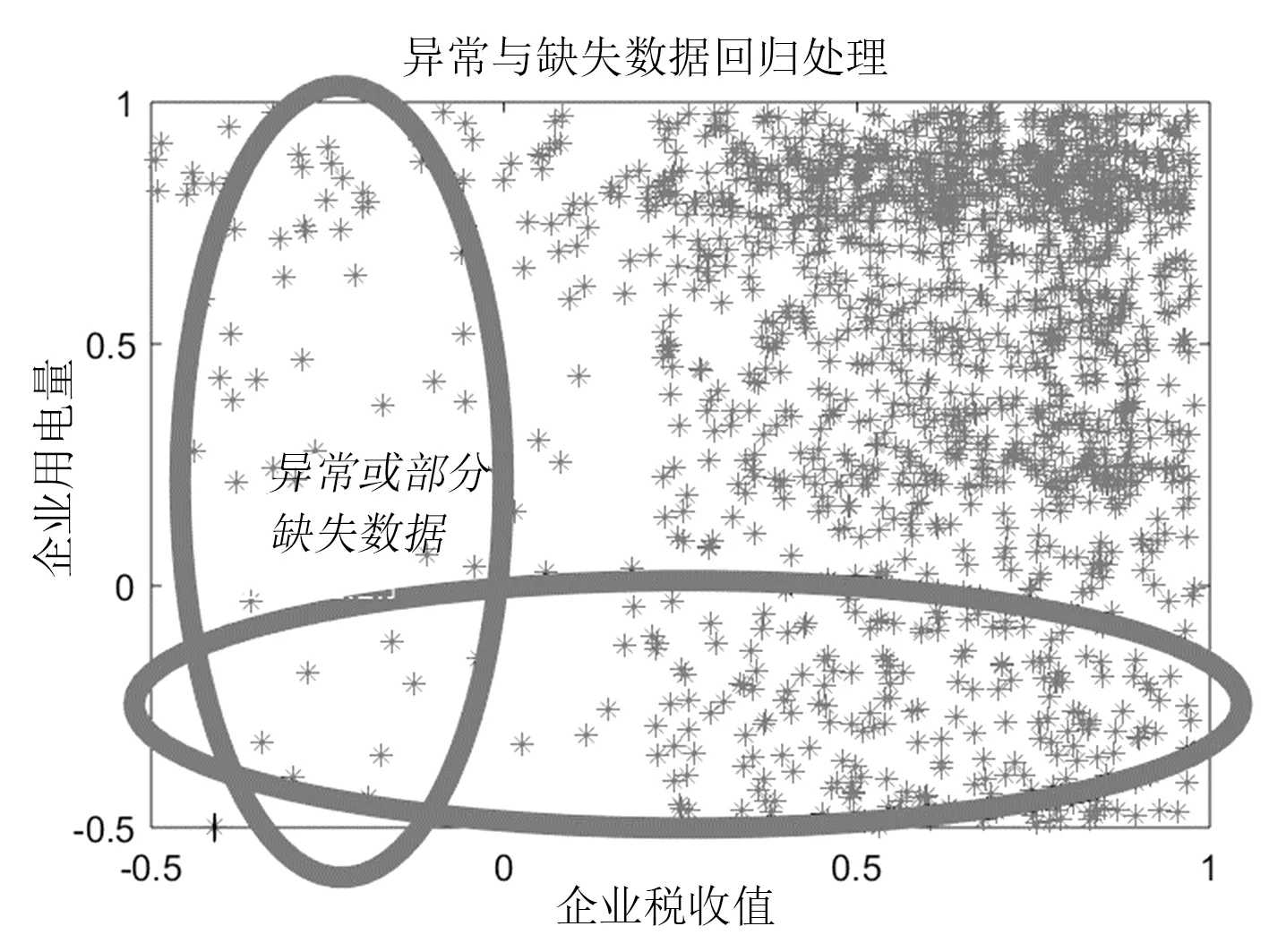
图3 异常与缺失特征辨识

图4 异常与缺失特征回归处理

2.4 核函数非线性映射

使用非线性映射φ把训练数据映射到一个高维特征空间，然后在高维特征空间里进行线性回归，映射回原空间后就成了输入空间的非线性分类。用核函数K(x，y)就可以实现非线性回归，如图5所示。

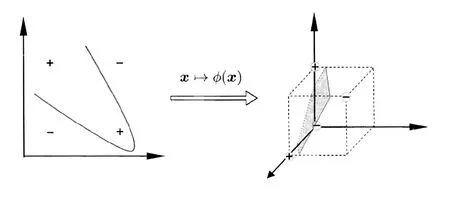
图5 核函数的非线性映射

2.5 网格搜索与验证

采用网格搜索法来选择了441组超参数(即不同的C，γ，ε组合),一组超参数可以确定一个SVM模型，选择网格搜索多个超参数以提高模型的边化能力，C为惩罚因子，γ为核函数的参数，ε为一个大于0的常数。在使用相同数据集的情况下，训练了441个不同的SVM模型。用一部分数据来做验证，避免过拟合。通过网格搜索得到的441个模型，在验证集上取误差最小的前25个模型，测试数据的最后结果取25个回归模型的平均值。

网格搜索法是一种直接的方法，它将不同组合的γ、C和ε值逐个进行测试，查看情况，网格搜索中，令：

C=(2(-5),2(-3),2(-1),2(1),2(3),2(5),2(7),2(9),2(11))

γ=(2(-15),2(-13),2(-11),2(-9),2(-7),2(-5),2(-3))

ε=(2(-15),2(-13),2(-11),2(-9),2(-7),2(-5),2(-3))

(7)

不同的参数组合依次求解，得到最优的超参数。

基于组合支持向量回归的排污企业生产识别流程如图6所示。

图6 基于组合支持向量回归的排污企业生产识别流程

3 测试结果分析

对企业1500个实际生产数据进行测试识别。输入数据为这1500个实际生产下的纳税值和用电量，其中，输入数据存在部分缺失和异常。组合支持向量机模型给出对于1500个输入特征下对应的生产判断。

输入的数据中，纳税数据小于0时为异常值，纳税数据为0时为缺失值。异常值和缺失值都是因为实际管理等原因造成的真实数据不能查询。

输入数据的总数为1500个，异常即小于0的数据为313个，占总输入数据的20.87%;部分缺失数据数量为29个，占总输入数据的1.93%，如表1所示。

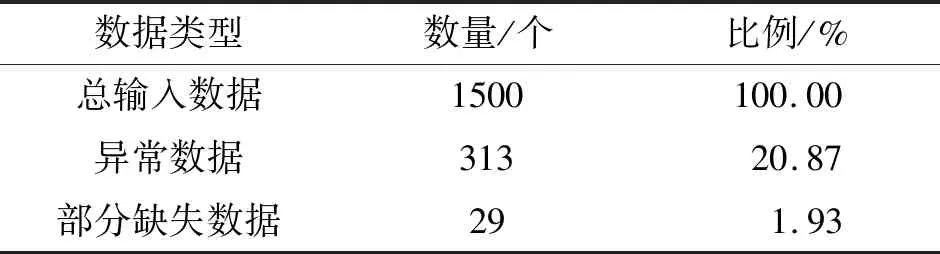
表1 输入数据分析

通过回归模型对异常数据进行处理，如图7所示，异常和部分缺失输入数据进行回归处理后，其规则化后的范围为(0,1)。

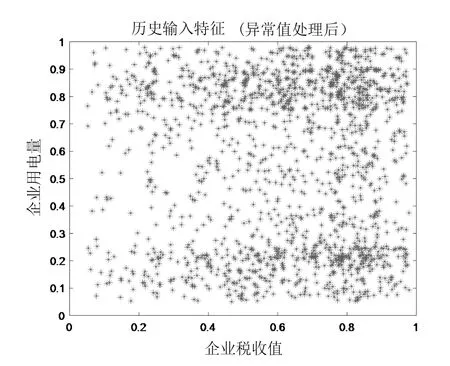
图7 异常和部分缺失数据处理后的输入特征数据

通过组合支持向量回归模型对异常和部分缺失值处理后的数据进行生产状态识别，结果如图8所示。

组合支持向量回归模型识别企业生产状态结果如表2所示。其中，正确识别的生产状态1484个，识别正确率为98.93%，多个支持向量机组合模型具有分类精度高的特点。由于异常和部分缺失数据有342个，未进行异常和缺失值处理时，正确识别1142个，识别正确率为76.13%，异常和缺失值回归处理提高企业生产状态识别率22.8%。

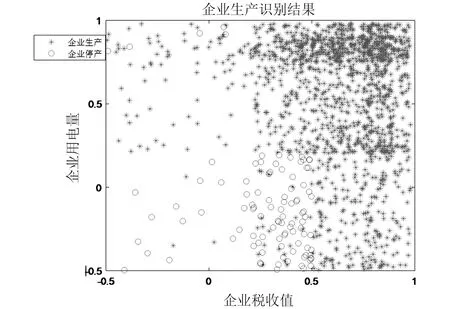
图8 企业生产状态识别结果

表2 组合支持向量回归模型识别企业生产状态结果

4 结 语

提出了一种综合考虑企业用电和纳税信息的污染企业生产状况识别方法。该识别方法考虑了实际应用过程中的数据部分病态的问题，采用回归分析，解决输入特征异常和部分缺失的问题，提高了分析结果鲁棒性；同时，通过网格搜索选择多个支持向量机组合模型识别污染企业生产状况，增加了模型的泛化能力，提高了分类精度。