电网超低频振荡影响因素综合分析与抑制措施研究

贺子润，陈 振2，邢昊中

(1.输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆 400044；2.国网四川省电力公司电力科学研究院，四川 成都 610041)

0 引 言

2019年6月，西南电网与华中电网正式异步联网运行，西南电网的水电占比高达70%以上，超低频振荡风险十分显著。当发生超低频振荡时，系统内所有机组共同振荡，频率和功率也发生持续振荡，突出特点是振荡频率低、振型特殊，所有机组转速同调变化，无明显的机间振荡,是一种与传统低频振荡机理完全不同的振荡。

目前对于超低频振荡的研究主要从机理分析和控制措施方面开展研究。

1)在机理分析方面：文献[1]在孤岛系统中分析了水轮机调速器等参数对振荡的影响。文献[2]通过对大量试验数据及水轮机调速器模型分析得出水电机组一次调频是产生超低频振荡的直接原因。文献[3]通过建立典型孤岛送出系统，利用特征根分析和时域仿真方法对超低频振荡模式进行排查和分析；并通过灵敏度分析，研究了水轮机引水系统水锤效应时间常数、调速器参数对超低频振荡的影响。文献[4]分别在单机系统研究了一次调频过程不稳定导致的超低频振荡事件，研究超低频振荡的振荡频率、阻尼、振荡表现等特征，并引入伯德图方法分析详细模型下的振荡频率和阻尼。文献[5]进一步研究多机系统的超低频振荡的分析，并提出相应的等值方法。文献[6]利用值集法提出了一套用于超低频振荡稳定分析的多参数图形分析工具，并研究水轮机特性系数对稳定性的影响。文献[7]利用复转矩系数法研究了超低频振荡产生的机理以及水轮机调速器、汽轮机调速器、负荷模型和系统惯量对超低频振荡的影响，并将超低频振荡归类为小干扰频率稳定范畴。文献[8]分析了水轮发电机调速系统对超低频振荡的影响及模型适用性问题。

2)在控制措施方面目前主要采用以下两种措施：一是调整水电机组调速器参数，其优点是从源头治理超低频振荡，并不影响水电消纳。文献[9-10]通过调整调速器PID参数大小实现超低频振荡的有效抑制，然而该方法的缺点是降低了水电调节速度，影响调频能力。为解决此问题，文献[11-12]同时考虑超低频振荡抑制和一次调频性能的影响，建立调速器PID参数的优化模型，在抑制超低频振荡和维持调频能力间取得平衡。二是直流附加控制措施。文献[13]通过时域仿真，提出了直流附加频率控制的参数设计原则。文献[14]提出超低频振荡的多直流协调控制策略。利用直流进行控制的缺点是会将送端的扰动传递给受端，造成受端的功率波动，影响受端电网的安全稳定运行。

为综合分析超低频振荡的影响因素并提出相应的控制措施，首先建立超低频振荡分析的单机带负荷模型，并基于稳定域的思想综合分析了电网超低频振荡的影响因素。在此基础上，考虑水锤效应的不确定性，建立了调速器参数的优化模型，并提出优化模型的智能求解方法。

1 超低频振荡影响因素综合分析

1.1 超低频振荡分析模型与方法

单机带负荷系统是分析频率稳定的最简单系统，反映了系统发电和负荷之间的平衡及有功频率控制的动态过程。基于单机带负荷系统，分析系统发生超低频振荡的产生机理，其方框图如图1所示。

图1 单机带负荷系统

发电机的转子运动方程：

(1)

式中：TJ为发电机惯性时间常数；Δω为发电机的转速偏差；ΔPm为原动机的机械功率输出偏差；ΔPe为发电机的电磁功率偏差；D为发电机的阻尼系数。

若忽略系统网损，仅考虑负荷的频率变化，则有

ΔPL=ΔPe=KLΔω

(2)

式中：ΔPL为负荷的有功变化量；KL为负荷频率调节效应系数。

由式(1)、式(2)可得发电机和负载的传递函数为

(3)

因D和KL的作用相同，可令Ds=D+KL。

水轮机的传递函数为

(4)

式中：Δμ为水轮机的导叶开度偏差；TW为水锤效应时间常数，其值随负荷变化，满载时TW取值为0.5～4.0 s。

目前，水轮机广泛使用并联型比例-积分-微分(proportion integration differentiation,PID)调速器进行调速，通过比例环节、积分环节、微分环节并联共同控制水轮机的导叶开度，这里采用的并联型PID调速器其传递函数为

(5)

式中：KP为调速器的比例系数；KI为调速器的积分系数；KD为调速器的微分系数；bP为调差系数；Ty为伺服系统时间常数。

通过上述传递函数，可以构造一个含水轮机调速器系统的单机带负荷系统模型，用于分析超低频振荡的形成机理，其系统结构如图2所示。

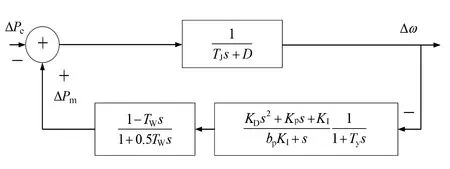
图2 水轮机组成的单机带负荷系统结构

超低频振荡分析方法主要包括复阻尼转矩方法与特征根分析方法。前者利用复阻尼转矩理论，将调速通道的阻尼转矩分解为同步转矩KmS和阻尼转矩KmD。阻尼转矩大于0，则表示调速通道提供正阻尼，否则提供负阻尼。阻尼转矩绝对值的大小，表明调速通道提供正/负阻尼的大小。后者建立系统的传递函数，通过求解特征多项式的解判断系统的稳定性，特征值实部大于0，表明系统失稳，否则表明系统稳定。

1.2 超低频振荡影响因素综合分析

利用稳定域的思想，对影响超低频振荡的因素进行综合分析。将各基本参数设置为：TJ=10 s，Ds=0.689，KP=0.5，KI=1.0，bP=0.04，Ty=0.2 s。分别设TW为0.5 s、0.7 s、0.9 s、1.1 s，在0～20范围内改变KP、KI，对每一组参数，若求得的特征根实部为负数，即系统稳定时，在(KP，KI)平面上画圈；若求得的特征根实部为正数，即系统不稳定时，在(KP，KI)平面上画叉，由此得到不同TW下KP、KI对系统稳定性的影响分布图，如图3所示。

由图3可知，当KP、KI一定时，增大TW，系统的稳定性显著变差；当TW、KI一定时，增大KP，系统的稳定性先变好，再变差；当TW、KP一定时，增大KI，系统的稳定性变差。

2 考虑水锤效应不确定性的调速器参数优化模型与求解

2.1 考虑水锤效应不确定性的调速器参数优化模型

由前述分析可知，引起电网超低频振荡的一个重要原因是调速器参数设置不合理从而导致调速器产生负阻尼转矩，通过优化调速器参数是抑制超低频振荡的一个有效手段。然而，现有致力于解决超低频振荡问题的水轮机调速器控制设计方法，更多地考虑了系统的稳定性，忽略了调速器需要承担跟踪负荷波动的任务，且调速器的稳定性与跟踪性能直接存在矛盾。因此需要在优化调速器阻尼性能的同时，考虑到调速器的跟踪性能。

另外，水锤效应时间常数TW也是影响水电为主电网超低频振荡的关键因素，其值的大小会随着发电机出力的改变而改变。然而，现有的调速器优化模型中，往往忽略了TW的变化，认为其值为定值，导致参数优化结果难以适应运行状态的改变。

为解决上述问题，根据历史数据的统计结果，对TW在取值范围内离散化处理，并得到确定各离散值对应概率的大小。这里假定TW离散概率分布如表1所示。

表1 TW的离散概率分布

另外，提出以误差平方和时间乘积积分(integral time square error，ITSE)准则刻画调速器的跟踪性能，其表达式为

(6)

式中，ΔPm,i(t)为第i种工况下，水轮机输入阶跃响应后，输入的时间响应与其稳态值之差。

在上述基础上，建立调速器参数优化模型：

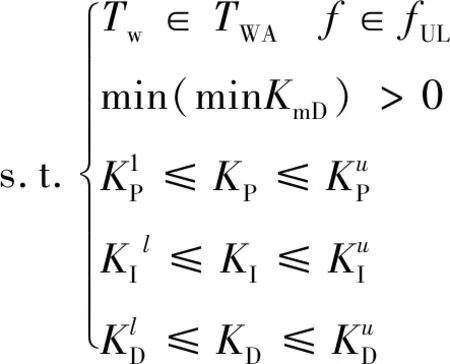
(7)

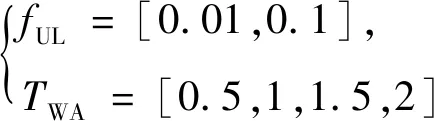
2.2 调速器优化模型求解

利用粒子群优化(particle swarm optimization,PSO)方法对上述参数优化模型求解，基于PSO的调速器参数优化模型的求解流程如图4所示。

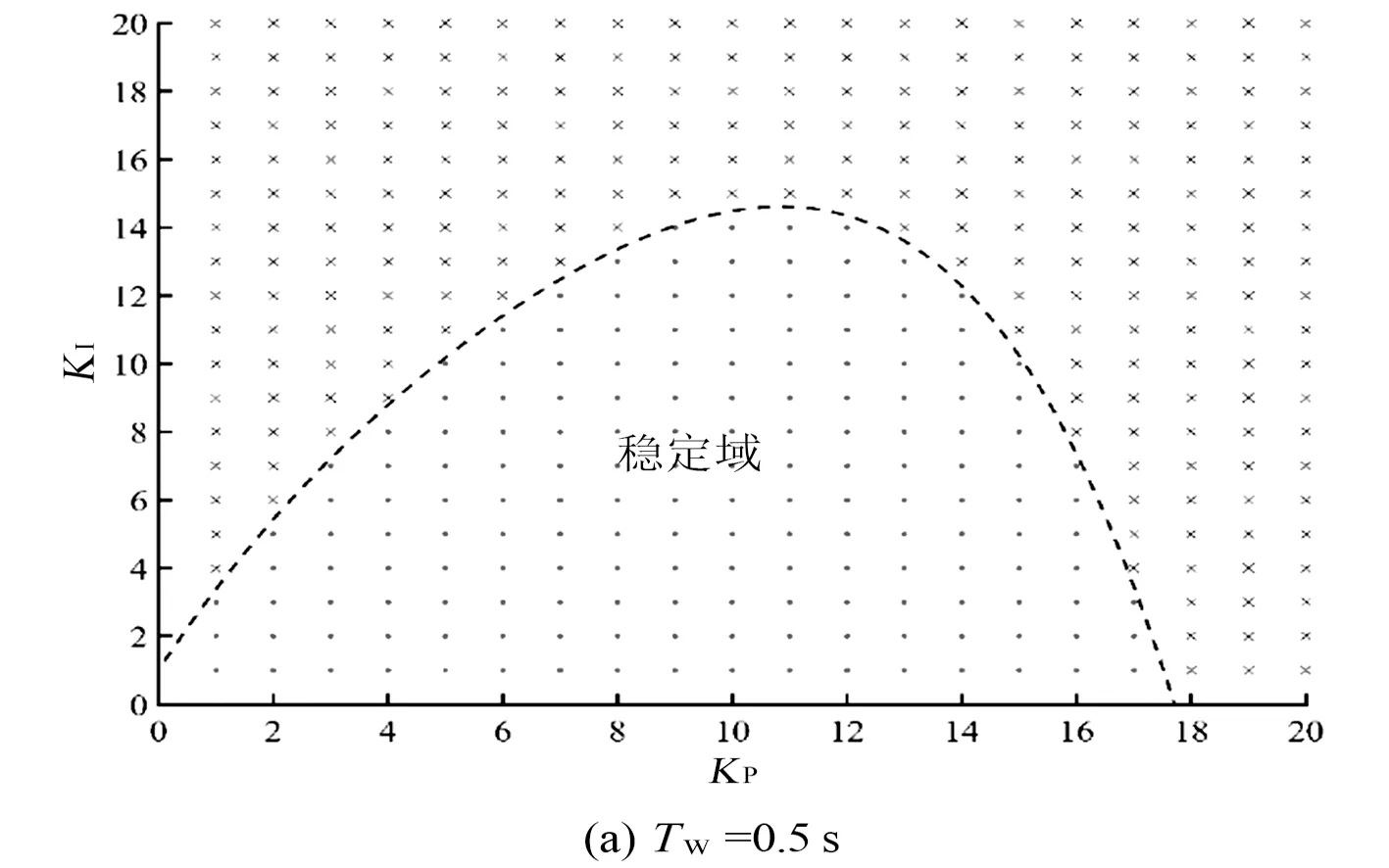
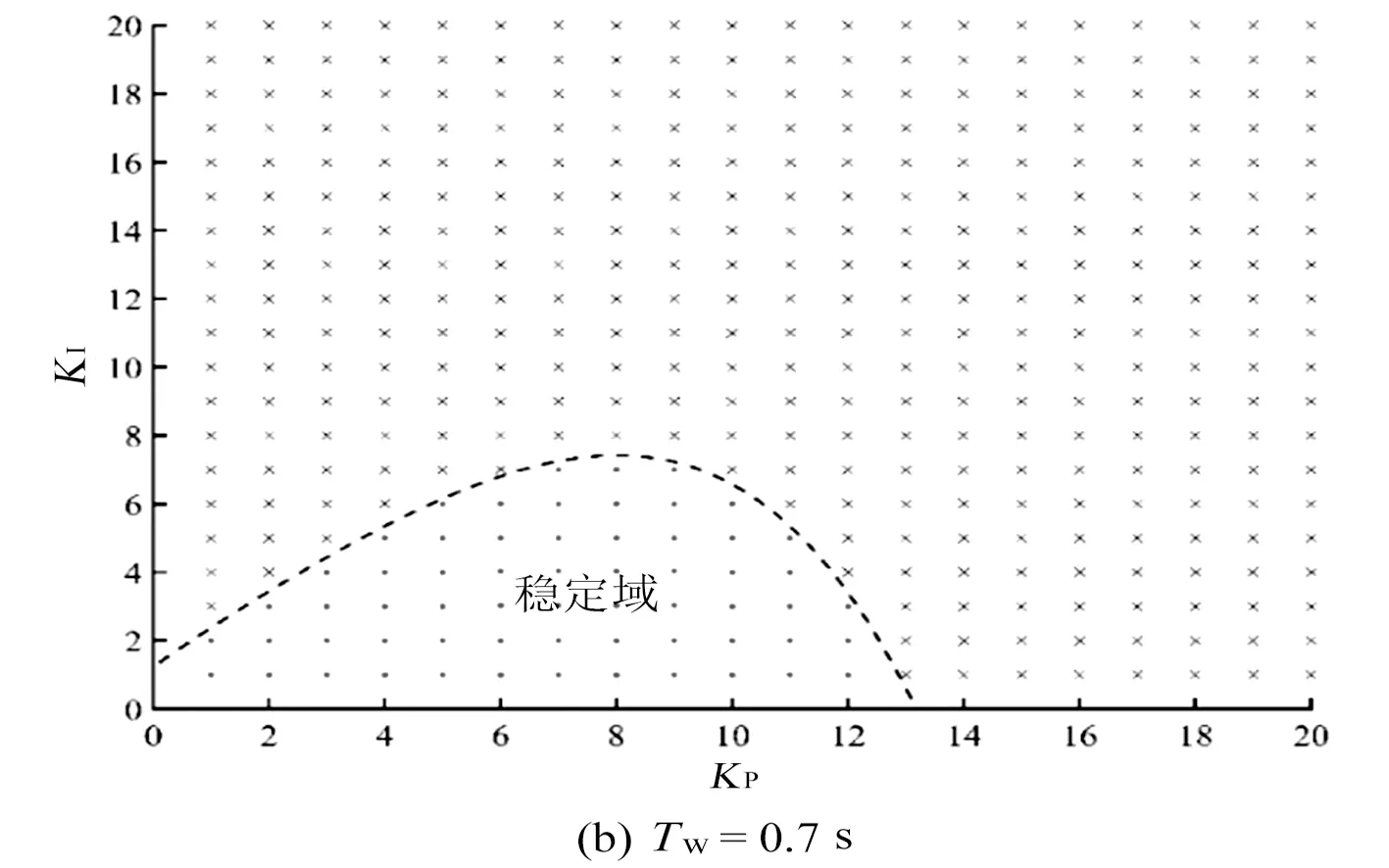
图3各参数对超低频振荡稳定域的影响

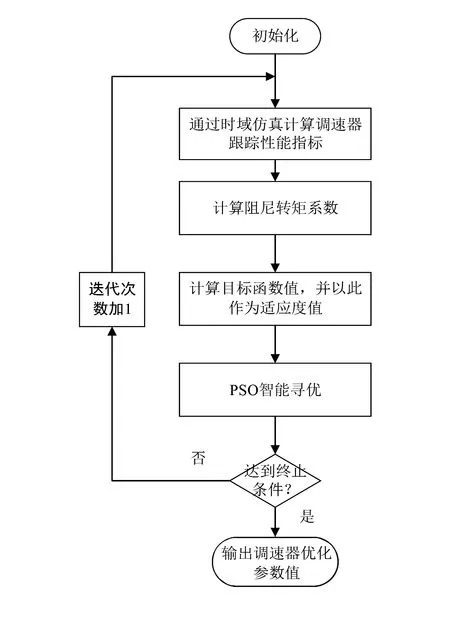
图4 调速器参数优化模型求解流程

3 算例验证

对于超低频振荡问题，由于多机系统可以解耦成单机系统进行分析，因此以图1所示的水轮机组单机带负荷为例来验证所提调速器参数优化算法的有效性。设定调速器的原始参数分别为KP=0.8、KI=1.2、KD=1.0。调速器参数的取值范围均取为[0,5]，利用所提模型进行调速器参数优化，调速器参数分别为KP=5、KI=2.32、KD=5。

在4种不同TW取值下，参数优化前后水轮机-调速器通道在超低频段的阻尼转矩系数对比和参数优化前后的系统阶跃响应曲线对比，分别如图5、图6所示。

由上述对比可知，所提方法能有效提升水轮机的阻尼系数，防止出现负阻尼的现象，从而避免系统发生超低频失稳。另外，由于在优化模型中考虑了多种运行工况下的TW值，因此参数优化结果具有一定的鲁棒性。

4 结 语

1)由超低频振荡影响因素综合分析可知，当KP、KI一定时，增大TW，系统的稳定性显著变差；当TW、KI一定时，增大KP，系统的稳定性先变好，再变差；当TW、KP一定时，增大KI，系统的稳定性变差。

2)考虑水锤效应不确定性的参数优化模型能有效抑制超低频振荡现象，并且具有一定的鲁棒性。

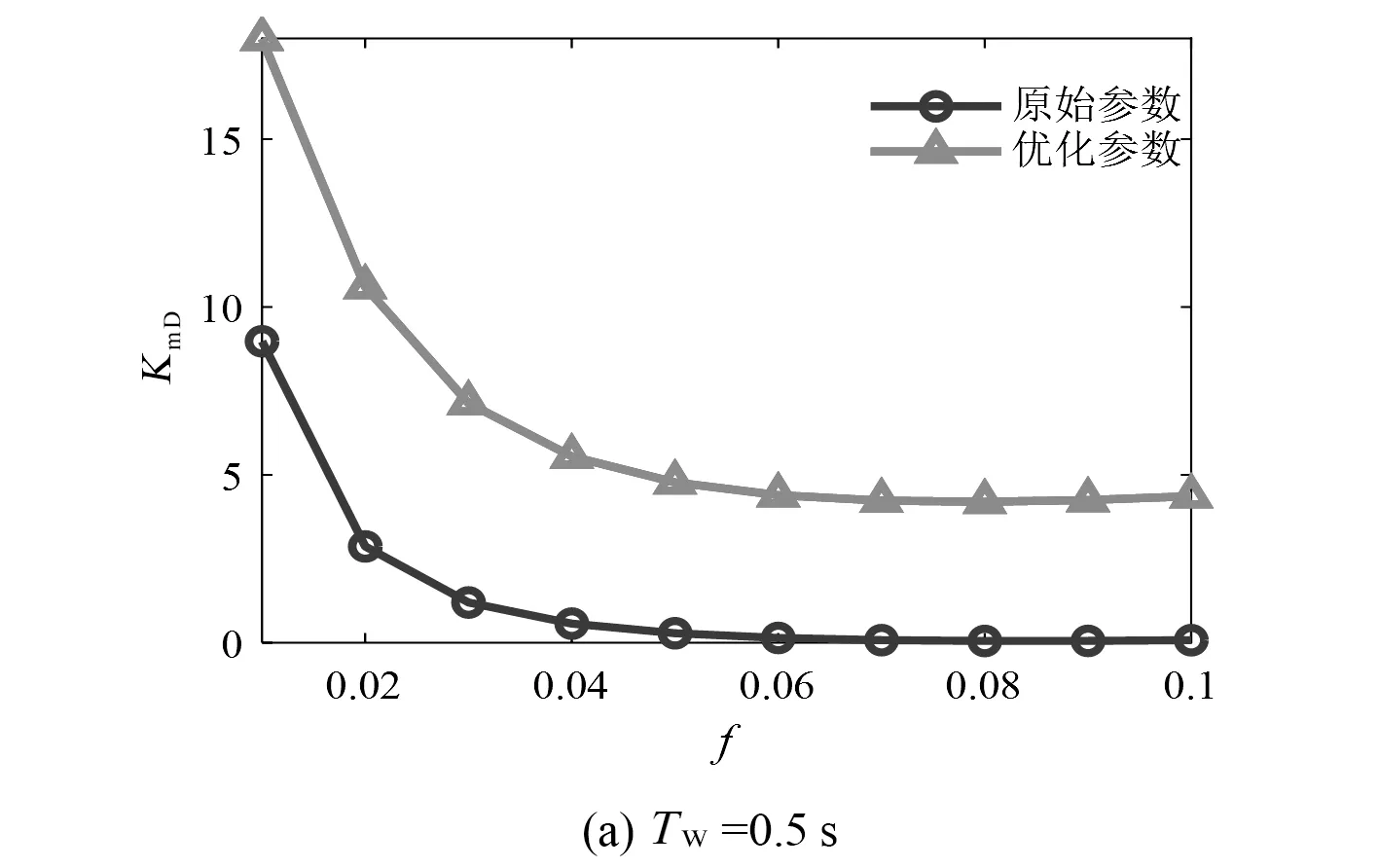
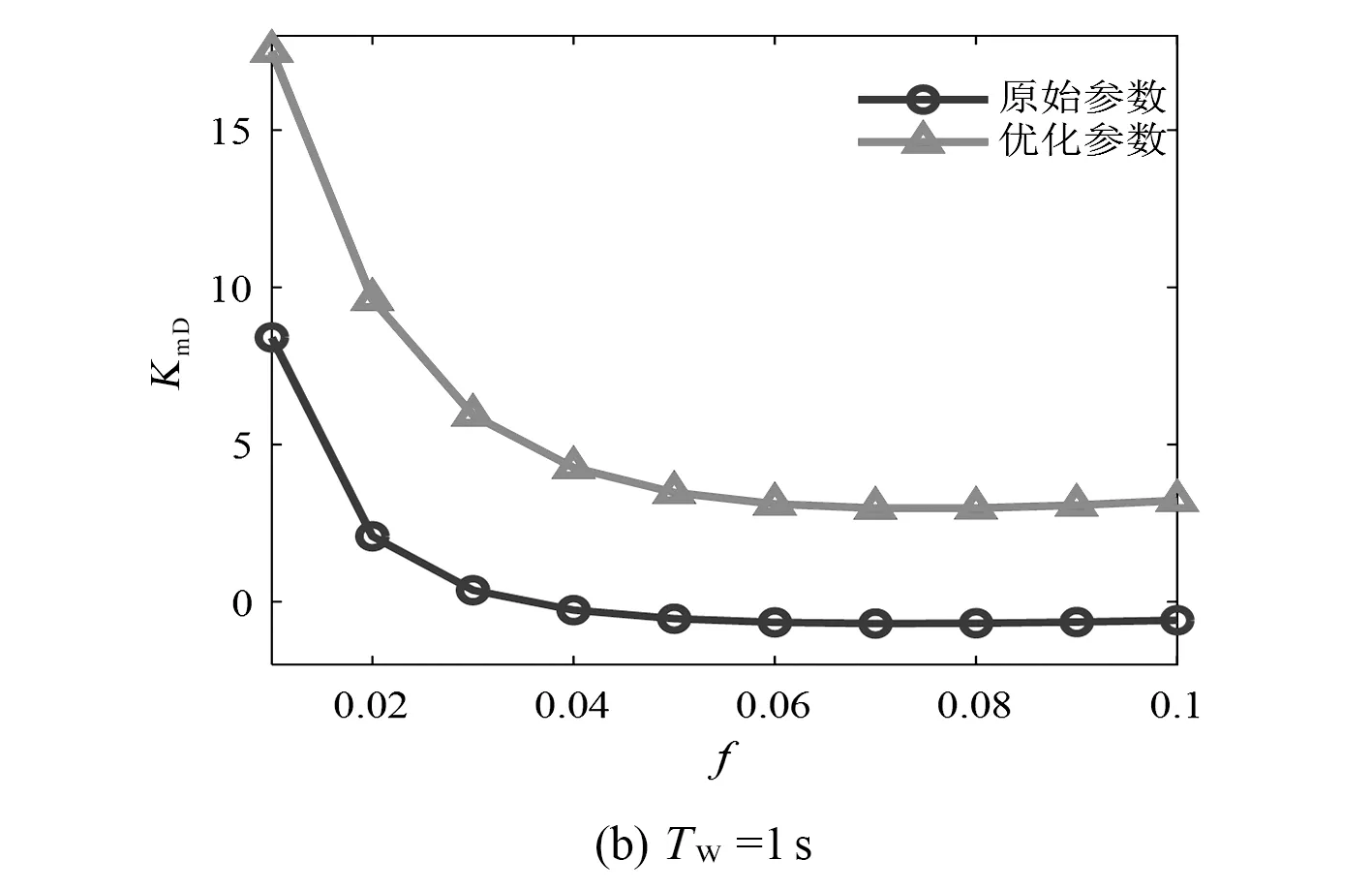
图5参数优化前后的阻尼系数对比

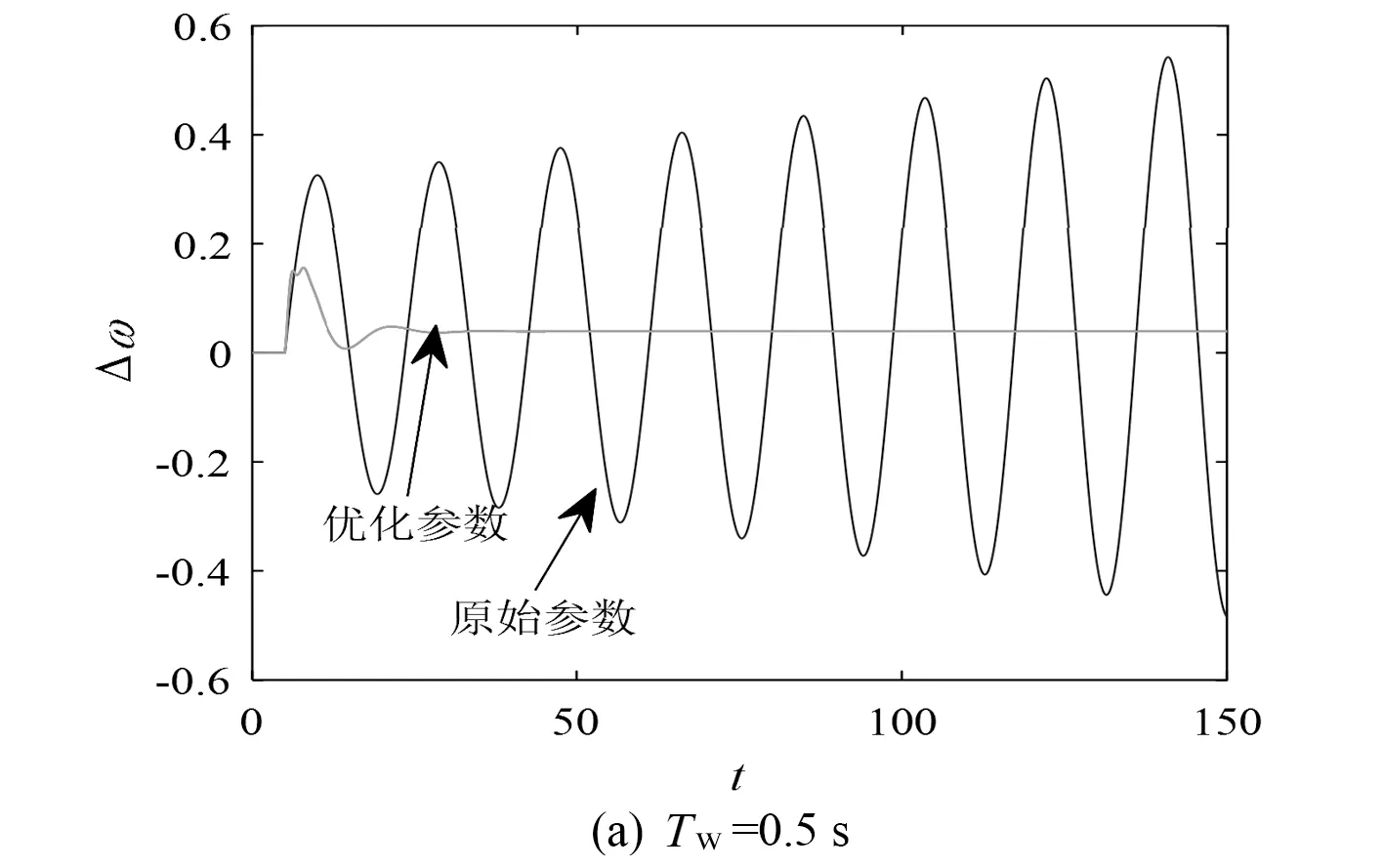
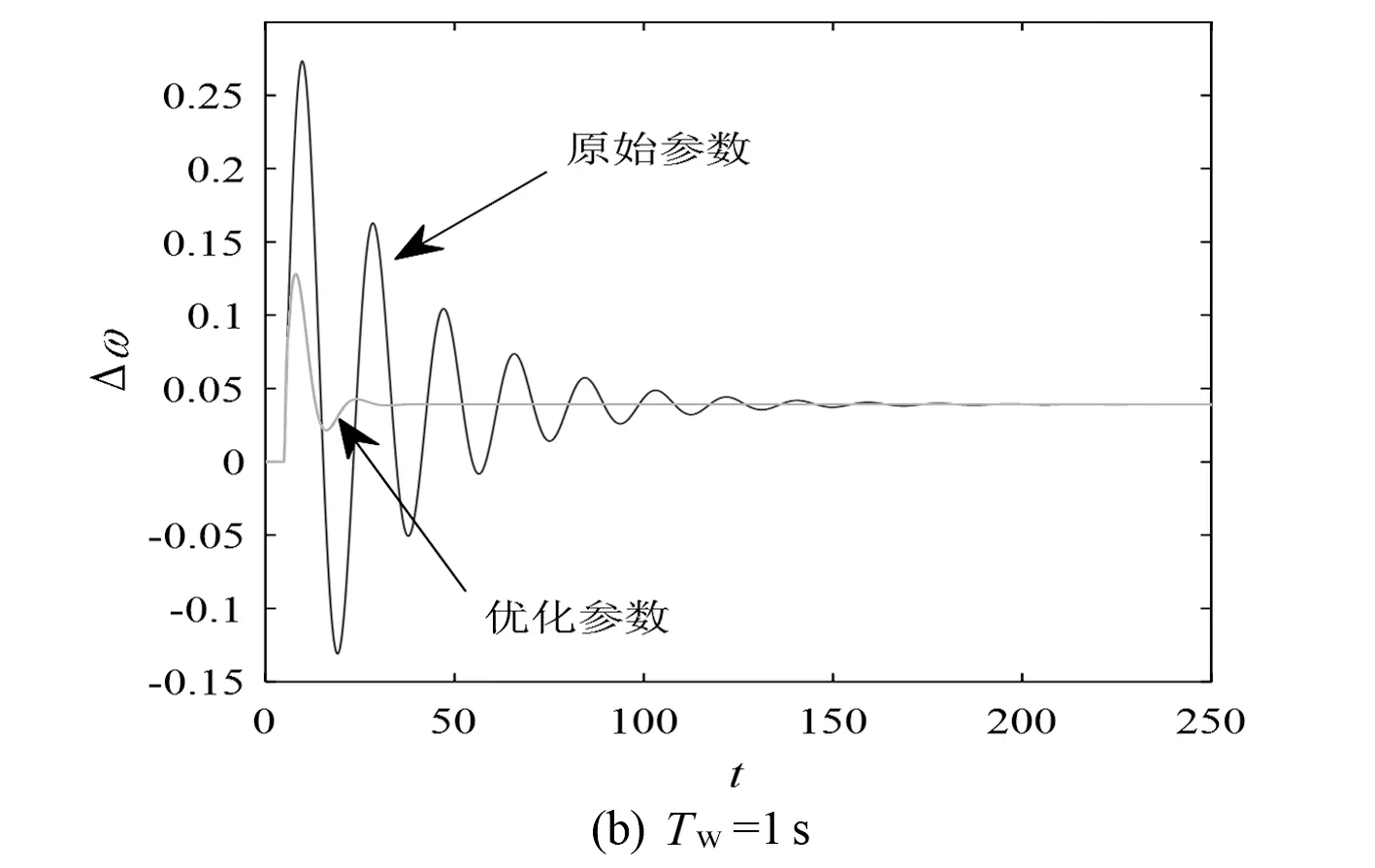
图6参数优化前后的阶跃响应对比