基于阻抗模型的集中式光伏电站谐波放大机理研究

(1.输配电装备及系统安全与新技术国家重点实验室(重庆大学)，重庆 400044；2.国网四川省电力公司电力科学研究院，四川 成都 610041)

0 引 言

受中国能源分布的影响，集中式光伏电站主要分布在西北偏远地区[1]，这使得光伏电站往往需要通过较长距离的输电线路才能上网。线路阻抗以及各级变压器会使电网与电站间产生负面交互作用，导致系统稳定性降低，电站输出谐波问题严重。因此，提高光伏电站输出电能质量、降低输出谐波电流含量，对于并网系统的安全稳定运行具有重要意义。这就需要对集中式光伏发电系统输出谐波的放大机理进行研究。

研究集中式光伏并网系统的谐波问题首先应对系统进行建模，然后再在模型基础上分析谐波放大的机理。国外较早就进行了针对交流系统的建模研究，文献[2]将直流系统中的阻抗建模引入到交流系统，将逆变系统、网侧系统分别进行诺顿电路、戴维南电路等效，然后就可以利用频域分析工具对系统进行研究。该方法提供了交流并网系统的建模工具，但是只建立了单机理想并网模型。

在国内，文献[3-5]将光伏电站各电气结构进行了等值建模，建立了输配电系统的等值电路，但是仅将逆变系统考虑为谐波电流源，忽视其内部控制环节。文献[6]提出诺顿等效电源系数表示逆变系统的内部控制环节，但是建模未考虑传输线路与升压变压器等结构。目前来看，针对光伏并网系统建模问题，研究主要集中在多逆变器并网结构或者分布式电站，鲜有对集中式光伏系统进行各结构充分建模[7-11]。

对于谐波放大的机理研究，文献[6，8]采用节点电压法求解了等值电路，得到谐波电流的数学模型。文献[3]则是认为系统的串并联谐振导致了谐波放大。文献[12-13]认为传输线路的分布电容效应会使并网系统出现宽频域谐振带。也有学者通过根轨迹与稳定裕度的分析，认为谐波放大受电网阻抗与光伏电站容量的影响[11，14-15]。

根据上述研究现状，充分考虑集中式光伏系统的各环节等效建模问题，建立并网系统的等值电路，在Matlab中绘制谐波电流的频域响应，并在Simulink中搭建光伏发电模型进行对比验证，进而揭示谐波放大的机理，为后续谐波抑制策略的研究提供理论基础。

1 并网系统的等值建模

目前集中式的光伏电站采用发电单元并联结构，通过站内母线汇集，然后经站内升压变压器及并网点主变压器升压，通过长高压输电线路上网。图1为电站电气结构，研究对象为50 MVA的集中式电站，发电单元由输出270 V直流的光伏电池阵列与LCL型的500 kW光伏逆变器和逆变器出口0.27/35 kV升压变压器构成，n个发电单元经35 kV母线汇流后通过35/110 kV主升压变压器接入高压输电线路上网。

构建集中式光伏发电系统的等值电路，需要对并网发电系统中的发电单元、各级变压器、传输线路、电网侧进行等值简化。采用电流控制的并网型逆变系统在具体阻抗模型中可以进行诺顿等效，电网侧可进行戴维南等效。图2为经过等值后从实际电气结构中提取的具体阻抗模型，其中变压器进行τ型等值，输电线路进行π型等值。

图2可经过电路变换进行简化，得到如图3所示的典型的诺顿等效电源与戴维南等效电源的互联阻抗模型。图2与图3中各符号及含义由表1给出。

图1 集中式光伏电站电气结构

图2 光伏发电系统具体阻抗模型

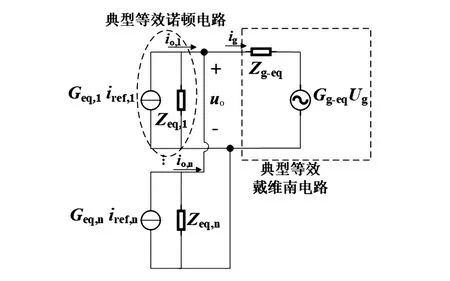
图3 光伏发电系统简化阻抗模型

下面进行等效诺顿、戴维南系数的整定计算。

诺顿等效电流源系数GS反映了逆变系统的控制策略，其值等于逆变器出口电流i2与参考电流iref的比值，即为电流环的闭环传递函数。图4为发电单元中逆变器的电流环框图。由图4可得到带有源阻尼的闭环传递函数GS(s)，如式(1)所示。

(1)

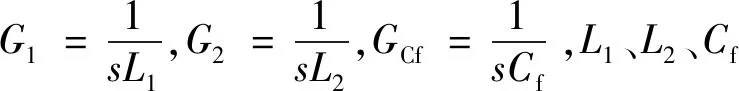
表1 电路各参数含义

图4 光伏逆变器电流环框图

各逆变器等效输出阻抗ZS等于输出电流i2与输出电压upcc的比值。图5为图4经变换后可反映upcc与i2的传递函数关系的框图。根据图5可计算逆变器的等效输出阻抗ZS，如式(2)所示。

图5 输出电压与输出电流的传递函数关系

(2)

Geq代表着简化后等效诺顿电源系数，如式(3)所示。

(3)

Zeq代表着简化后诺顿电源并联等效阻抗，如式(4)所示。

(4)

Zg-eq代表着简化后网侧戴维南电路的等效串联阻抗，如式(5)所示。

Zg-eq=(Zg‖Zp+ZL)‖Zp‖Z35M+Z35

(5)

Gg-eq代表着戴维南等效后的网侧等效电源系数，如式(6)所示。

(6)

考虑n台发电单元并网运行的情况，利用节点电压法可对图3中的节点电压Uo进行求解。节点电压方程如式(7)所示。

(7)

又因为并联系统中任一台发电单元(以第j台表示)诺顿等效电源满足式(8)：

Io,j=Geq,jIref,j-Yeq,jUo

(8)

通过消去节点电压Uo，可以得到单个发电单元输出电流Io,j的表达为

(9)

式(9)分为3个部分，可以看出发电单元输电电流受自身参考电流、其他并联发电单元参考电流以及电网电压3个因素影响。

对于集中式光伏电站，更关注其入网电流Ig的情况，因此对式(9)的Io,j进行求和得

(10)

假设各发电单元完全一致，则式(10)可简化为式(11)：

(11)

式(11)与式(8)类似，均为Ig=GIref-YUg形式，说明入网电流Ig受集中式电站等效系数G和电站与电网等效耦合导纳Y的影响，在系统阻抗模型中，考虑50 MVA集中式光伏电站的情况，即台数n将固定，那么G和Y与传输线路阻抗有关，即受传输线路长度的影响。

2 谐波放大机理分析

利用Matlab对前面已建立的集中式等效电源系数G和电站与电网等效耦合导纳Y进行频域分析，思路是不断改变输电线路长度，可以得到一系列系数G和Y的幅频响应曲线，然后利用绘图工具将曲线簇放在同一坐标轴系内，绘制出等效电源系数G和电站与电网等效耦合导纳Y随输电线路长度变化的幅频响应特性图。仿真算法流程图如图6所示。

图7为系数G和Y随输电线路长度变化的幅频响应图。

图7说明了3点：1)谐振尖峰频率点会随着线路长度增加而向低频段移动；2)输电线路的分布电容效应会使得同一线路长度下系统产生多个谐振点，体现为图7中的环形带；3)等效电源系数G对入网电流的影响远高于等效耦合导纳Y的影响，电网电压通过等效耦合导纳Y对入网电流施加的影响较小。根据幅频响应图，可以大致得到响应幅值与频率和长度的对应关系，比如在60 km馈线长度与19次谐波处存在一个谐振尖峰，说明该电站模型网侧的19次左右的谐波电流含量将受到较大程度的增加。

图6 仿真计算流程

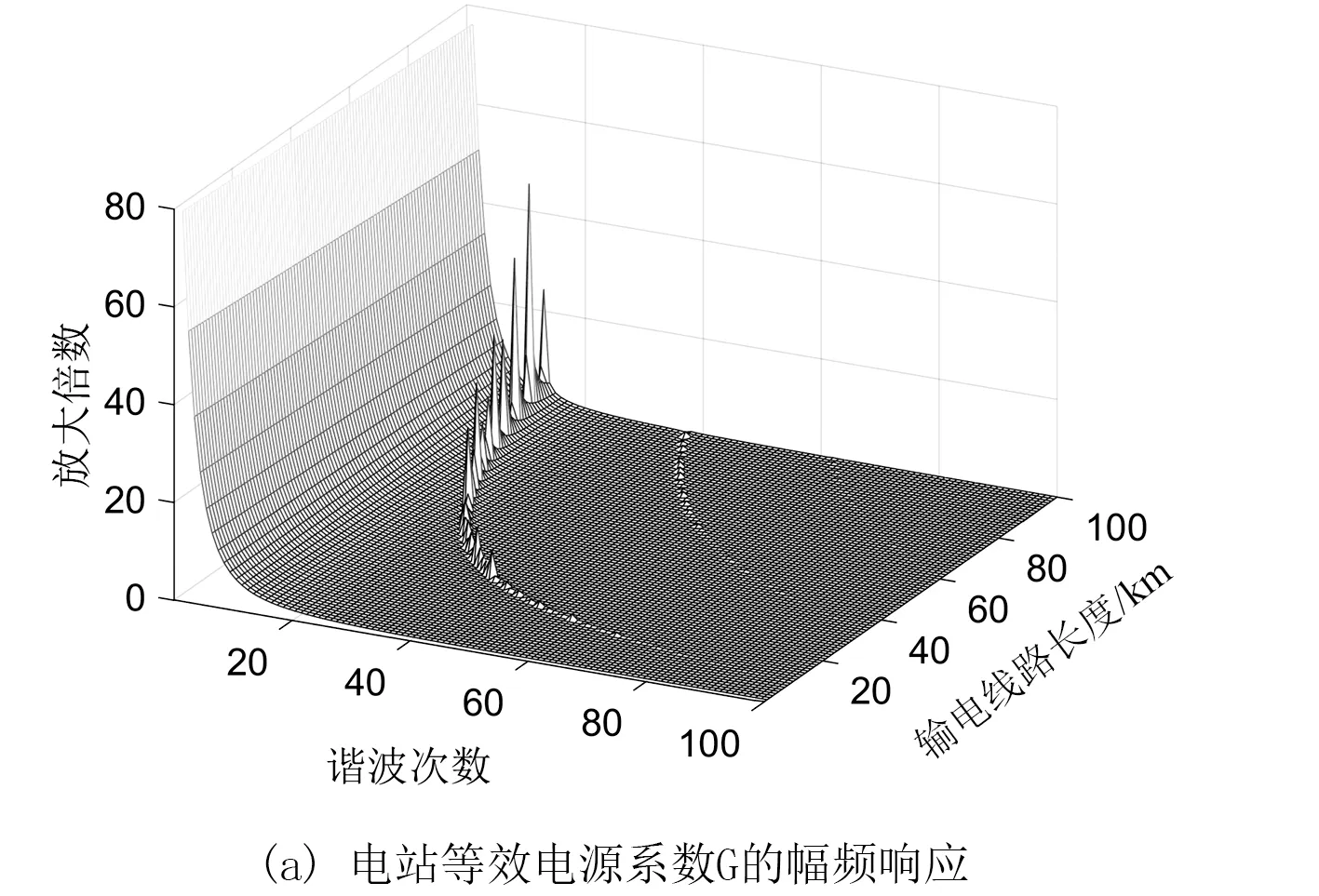
图7 系数G和Y随输电线路长度变化的幅频响应

3 仿真对照分析

为了更好说明集中式光伏电站输出谐波放大的问题，按照图8的结构在Simulink中搭建容量为50 MVA的电站仿真模型。

图8 光伏电站仿真模型结构

图9为单个发电单元仿真模型的控制结构。该模型的发电单元为单级式三相LCL逆变器，采用电容电流反馈阻尼以及网侧电流闭环控制，由电压外环提供电流环给定值。

图9 光伏逆变器的控制策略

光伏电池组采用Simulink中由ISoltech厂商提供的模型，型号为lSTH-220-P，单块额定功率219 W，最大功率点电压29.3 V，最大功率点电流7.47 A，开路电压36.6 V，短路电流7.97 A，串联单元19个，并联单元120个。MPPT采用定电压跟踪策略，使直流母线电压Udc维持在最大功率点557 V左右。发电单元相关参数如表2所示。

假设各发电单元完全一致，那么可以将50 MVA的电站模型进行单机等值，以便在Simulink中运行。

通过仿真，可以得到不同线路长度下，逆变器出口电流与网侧电流的波形与频谱分析。图10至图12分别为30 km、60 km、80 km时的仿真结果。

表2 仿真参数设置

图10 线路长30 km时仿真结果

图11 线路长度60 km时仿真结果

从图10至图12可以看出，谐波电流在传输过程中普遍存在放大现象，不同长度的线路影响着不同频率的谐波，且影响程度也不同。在网侧电流频谱中标注出了被明显放大的谐波，其频率位置与图7幅频响应图大致对应。

以图11线路长度为60 km时的仿真结果为例进行分析，从图11(d)可以看出，受到较明显放大的网侧谐波电流频率主要在11～23次谐波。下面将仿真波形与第2节幅频响应曲线图进行对照。

表3给出了图7中线路长度为60 km时等效电源系数G和等效耦合导纳Y的响应幅值。

表3说明了当输电线路为60 km长度时，系统的谐振尖峰处在11、13、17、19、21、23次，其中最高谐振尖峰处在19次。

表4给出了在线路长度为60 km的情况下，逆变器出口电流与网侧电流中处在该频次范围的谐波电流含量。

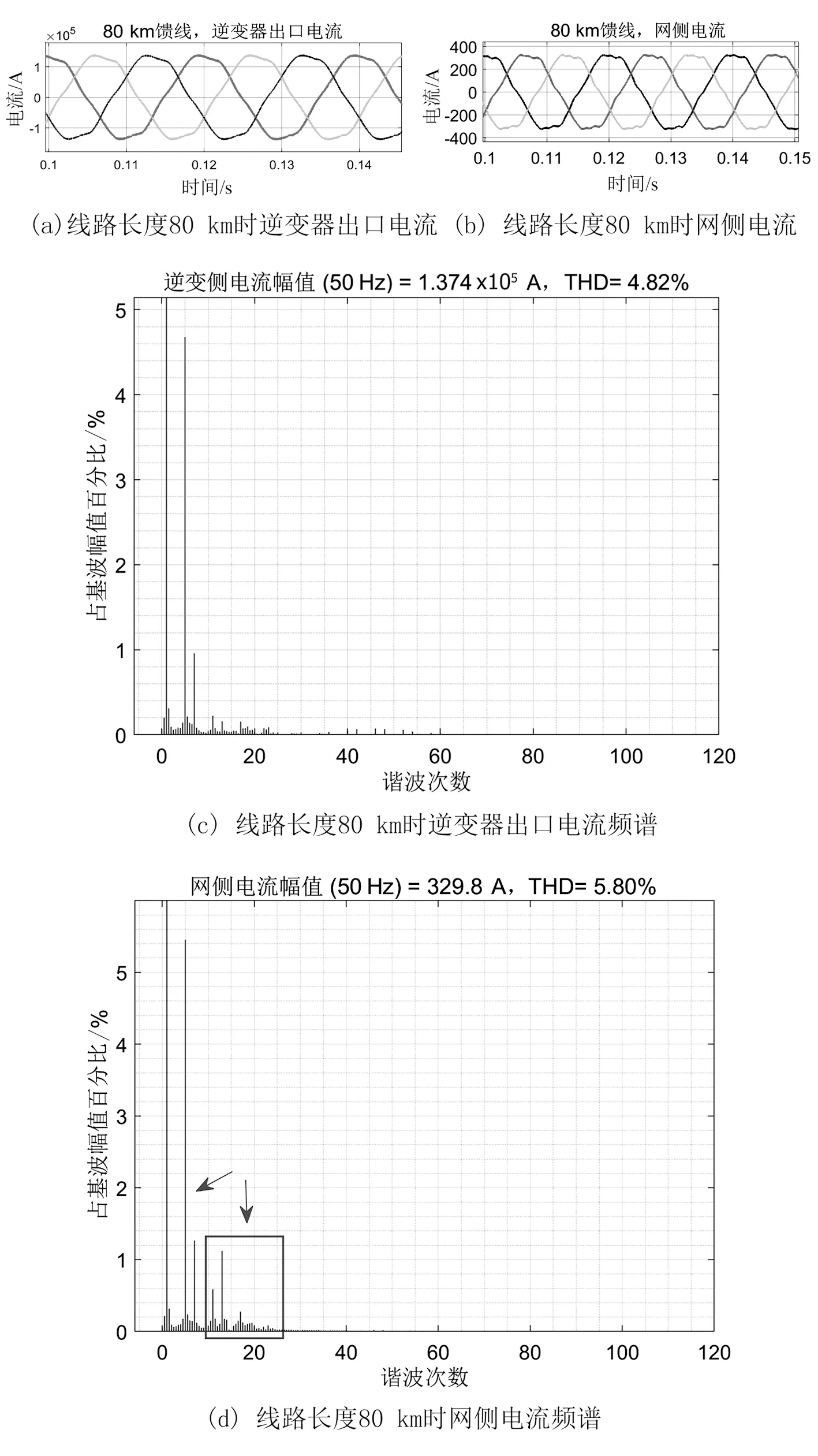
图12 线路长80 km时仿真结果

表3 等效电源系数G和等效耦合导纳Y幅频响应幅值

表4 逆变器出口电流与网侧电流中各次谐波的含量

从表4可以看出，线路长60 km时，17、19、21次谐波的放大倍数较为突出，其中19次谐波放大程度最严重，这与表3的结果相符，但是11、17次谐波的放大倍数与表3结果相比偏大，可能是由于在建立Simulink光伏电站开关仿真模型时，控制器效果不够理想导致的谐波含量数值上的偏差。

4 结 语

以50 MVA的集中式光伏电站为研究对象，建立了集中式光伏电站的等效阻抗模型，并在阻抗模型基础上研究谐波电流放大的机理。得出以下结论：

1)集中式光伏发电系统的谐振频率会随着传输线路长度的增加而逐渐向低频偏移，输电线路的分布式电容会使得系统幅频响应出现环形谐振尖峰带。

2)系统阻抗模型可以简化为Ig=GIref-YUg形式，仿真分析表明谐波电流受等效电源系数G和等效耦合导纳Y的影响，幅频响应图中的尖峰频率对应着受到严重放大的谐波电流频率。

3)在后续研究抑制策略时，可通过改变系统阻抗模型中的等效电源系数G和等效耦合导纳Y，抑制幅频响应图中的尖峰，就能使系统谐波电流含量降低。可从外接滤波装置以达到系统阻抗重塑，亦或直接改变逆变器控制策略从而修改等效电源系数G两个方向进行研究。