基于混合图模型的统计学课程关系分析
袁 蕾, 徐平峰, 单 娜
(1.长春工业大学 数学与统计学院, 吉林 长春 130012;2.东北师范大学 心理学院, 吉林 长春 130024)
0 引 言
本科教育在人才培养工作中占据基础地位,抓好本科教育,提高学生的学习成绩是一个重要方面。在每个专业的学习中,必然涉及到多门课程,分析这些课程之间的关系,既有助于教师教学,也有利于学生学习。
近年来,各个专业的老师从本专业知识体系出发,研究了课程之间的关系。例如,翟志强[1]分析了思想政治理论课课程体系中四门核心课程之间的内在关系;向少华[2]从课程关系研究基本乐理课程教学内容的改革;周华[3]从课程关系研究高职“职业通用能力”培养的课程体系。此外有学者从学生的考试成绩出发,利用数学模型或统计学模型研究课程关系。例如,赵慧等[4]利用高斯图模型分析力学、向量、代数、分析和统计5门百分制课程的关系;郝立丽等[5]分析了大学10门数学课程的成绩,将所有课程的分数以中位数为阈值变为二值型数据,然后利用遗传算法和K2算法构建大学数学课程贝叶斯网;张翼等[6]选择课程数据库部分文本数据,利用贝叶斯网反映课程之间的关系,以解决职业教育在课程内容安排上的实时性决策问题;王福友[7]利用含潜变量的有向无圈图模型分析了百分制课程的结构关系。
文中利用混合图模型分析某高校统计学专业学生的考试成绩,进而刻画各门课程的关系,为教师修订培养方案和教学大纲及课程建设提供参考,为学生的学习及选择研究方向提供依据。
1 混合图模型
学生成绩多为百分制和5级制,也就是既有数值型分数,也有分类型分数。为此,考虑同时包含分类变量(也称为属性变量)和连续型变量的混合图模型。混合图模型被广泛用于生物信息学、机器学习等领域, 详见文献[8-10]。文中的定义和概念主要参考文献[8]。
设有p个属性型随机变量X=(X1,X2,…,Xp),每个变量取有限个属性值,令|Xi|表示Xi的取值个数。设有q个连续型变量,Y=(Y1,Y2,…,Yq)。假设(X,Y)的联合分布服从条件高斯分布,即X服从多项分布,给定X=x的条件下,Y服从正态分布N(μx,Σx)。若Σx不依赖x,则称为齐次模型,否则称为非齐次模型。在混合图模型中,以属性变量和连续变量为顶点,构建简单无向图G=(V,E),V为顶点集,E为边集。每个顶点表示一个变量,若两个变量在给定其他所有变量时是条件独立的,则在无向图中两个顶点间不连边,否则连边。这样构建的无向图与条件高斯分布满足马尔可夫性,同时图可直观地表示变量间的条件独立关系。
三角图、树和森林如图1所示。
图1 三角图、树和森林
文中考虑的无向图为强可分解的,即图为三角图并且不含禁行路,所谓三角图是指图中不含大于等于4元的无弦圈,禁行路是指首尾变量为属性变量,而路中间包含连续变量。
图中,灰色的点代表属性变量,白色的点代表连续变量。(i)中,路1,2,5和路4,3,2,5为禁行路。(i)和(ii)是三角图,而(iii)和(iv)不是三角图,因为它们至少有一个4元圈不含弦,即圈4,3,2,5,4。(i)不是强可分解的,因为有禁行路,而(ii)是强可分解的。强可分解模型的优点是其极大似然估计存在显式解,也是更加方便计算评价模型好坏的得分,例如似然、AIC、BIC等。
可分解模型的特例包括树或者森林,树是连通的无圈图,而森林是无圈图,一片森林可能包含多棵树,树与树之间是不连通的。图1中(v)和(vi)是树,但(v)不是强可分解的,因为它有禁行路4,3,2,5,而(vi)是强可分解的。(vii)是强可分解的森林,而(viii)不是强可分解的森林,因为它有禁行路1,3,4。树或森林模型比一般可分解模型简单一些,因而寻找最优的树或森林模型的计算复杂度比寻找可分解模型低很多,更加适用于高维变量情形,详见文献[9]。
设(X1,Y1),(X2,Y2),…,(XN,YN)为来自混合图模型的N个观测值。对于森林或者树模型G=(V,E),设L为似然的最大值,则对数最大似然正比于森林或树的所有边对应的顶点间的互信息之和,即
式中:Iv1v2----互信息。
两个属性变量Xu,Xv之间的互信息为
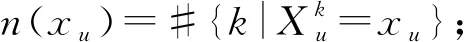
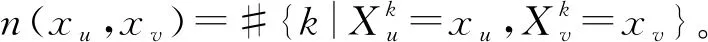
两个连续变量Ys,Yt之间的互信息为
属性变量Xu和连续变量Ys之间的互信息为Ius。
当考虑齐次模型时,
当考虑非齐次模型时,
令
于是,若定义森林或者树的权重为所有边的两个变量的互信息之和,则求最大似然的森林或树,等价于求权重最大的森林或树。
除了似然,AIC和BIC也可作为评价模型好坏的准则,它们分别为-2ln(L)+ln(N)r和-2ln(L)+ln(N)r。由似然与互信息的关系,经推导可得惩罚的互信息。两个属性变量Xu,Xv的惩罚互信息为
其中
kuv=(|Xu|-1)(|Xv|-1)。
两个连续变量Ys,Yt之间的惩罚互信息为
其中
kst=1。
属性变量Xu和连续变量Ys的惩罚互信息为
当考虑齐次模型时,
kus=|Xu|-1,
当考虑非齐次模型时,
kus=2(|Xu|-1)。
类似的,可以得到AIC惩罚互信息。若定义森林或者树的权重为所有边的两个变量的惩罚互信息之和,则最小化AIC和BIC准则的森林或树等价于最大化权重的森林或树。
对于森林或树模型,定义了边的权重后,可通过Kruskal或Prim算法求最大支撑森林或树。对于一般的强可分解模型,由于似然有显式解,所以不难得到AIC或BIC的值,但由于强可分解的模型较多,通常采用逐步向前贪婪搜索的方式找一个AIC或BIC局部最大的模型,详见文献[9]。上述方法可由R软件包“gRapHD”实现[9]。
2 课程结构分析
文中收集了某大学统计学专业101名学生的31门课程成绩,8门课程成绩为5级制,分别是计算机实习、数据库课设、认识实习、学科概论、多元统计课设、实验物理B、数学模型、计算机课设,其余23门课程成绩为百分制。采用混合图模型对31门课程的成绩进行建模,其中假设百分制成绩服从正态分布,假设5级制成绩服从多项分布,这里不考虑成绩的优、良、中、及格、不及格的顺序。
首先考虑齐次混合图模型。基于BIC准则惩罚的互信息得到了课程关系的森林模型和强可分解模型,分别如图2和图3所示。
图2 基于BIC准则的齐次森林模型
在两个模型中,5级制课程与百分制课程连接的边不多,可能由于5级制课程多数为实践类课程,而百分制课程为理论课,分别反映学生的实践能力和理论知识掌握能力。数学分析1、2、3联系比较紧密,数学分析3通过实用回归分析影响其他课程,并且概率论与数理统计、实用回归分析、抽样调查课程连接的边比较多,说明这些课程处于核心地位。图3比图2边多一些,描述了课程间更丰富的关系。
3 结 语
基于混合图模型分析某高校统计学专业本科生28门课程的成绩,刻画了各门课程的依赖关系,发现了部分核心课程。 希望文中得到的课程关系可为学生培养方案的制定和学习提供一定的参考。

