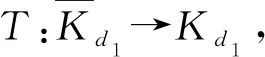
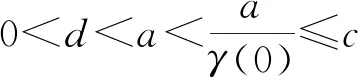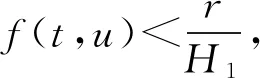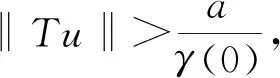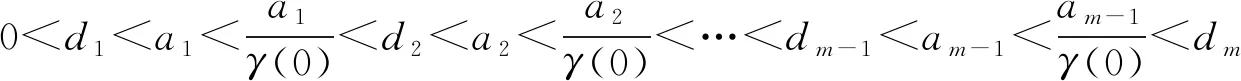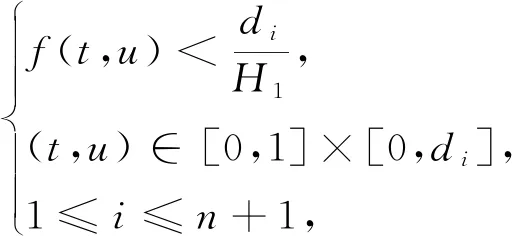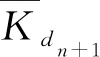非线性分数微分方程边值问题多个正解的存在性
岳俊瑞, 白庆月
(山西工商学院 计算机信息工程学院, 山西 太原 030000)
0 引 言
分数微积分在科学和工程学的许多不同领域中有着广泛应用,例如流体流动、流变学、电网络、化学物理、动力系统控制理论、光学和信号处理等[1]。
由于许多问题的讨论都可以归结为对非线性分数微分方程边值问题的研究,近年来,非线性分数微分方程边值问题解、正解的存在性或唯一性受到广泛的关注[2-13]。特别是Zhang[10]研究了非线性分数微分方程边值问题
文献[13]利用Green函数性质、上下解方法和不动点定理研究了非线性分数微分方程边值问题
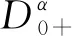
受以上文献启发,文中研究非线性分数微分方程边值问题
(1)
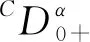
为了得到主要结果,给出一些基本概念和Leggett-Williams不动点定理[14]。
设K是Banach空间E中的锥,如果算子σ:K→[0,+∞)连续且对任意的x,y∈K和λ∈[0,1],有
σ(λx+(1-λ)y)≥λσ(x)+(1-λ)σ(y),
则称算子σ是K上的非负连续凹泛函。给定两个常数a,b,满足0 Ka={x∈K:‖x‖ K(σ,a,b)={x∈K:a≤σ(x), ‖x‖≤b}。 1){x∈K(σ,a,b):σ(x)>a}≠Ø且对任意的x∈K(σ,a,b),有σ(Tx)>a; 2)对任意的‖x‖≤d,有‖Tx‖ 我们给出分数微积分学理论的一些概念和结果,这些概念和结果可以从最近的文献[1]中找到。 假设N={1,2,3,…},α>0且[α]表示α的整数部分。 n=[α]+1,t>0。 其中 (2) 引理1设n由式(2)给出,且u∈ACn[0,1]或u∈Cn[0,1],则 c2t+…+cn-1tn-1, 其中,ci∈R,i=0,1,2,…,n-1。 在文中的剩余部分,假设α∈(2,3]是实数且f:[0,1]×[0,+∞)→[0,+∞)是连续的。 引理2设y∈C[0,1]是给定函数,则边值问题 (3) 有唯一解 其中 (4) 对任意的s∈[0,1],设 和 注释1[15]由函数γ定义不难得到对任意的s∈[0,1),有γ(s)≥γ(0)且γ(0)∈(0,1)。 引理3[15]由式(4)定义的Green函数G(t,s)具有以下性质: 1)对任意的(t,s)∈(0,1]×[0,1),有G(t,s)∈C([0,1]×[0,1))且G(t,s)>0; 设E=C[0,1],赋予其范数 且 K={u∈E:u(t)≥0,t∈[0,1], 则E是Banach空间且K是E中的锥。 定义K上的算子T为 u∈K,t∈[0,1]。 由于G(t,s)在s=1处奇异,需要说明算子T是有定义的。事实上,对任意固定的u∈K,有0≤u(s)≤‖u‖,s∈[0,1]。设 则f(s,u(s))≤L,s∈[0,1],结合引理3可得 G(t,s)f(s,u(s))≤LM(s), (t,s)∈[0,1]×[0,1), 引理4[15]算子T:K→K是全连续的。 为了方便,设 (5) (6) (7) 则边值问题(1)至少有三个正解u,v,w满足 ‖u‖ d<‖w‖, 证明 对任意的u∈K,定义 很容易验证σ是K上的非负连续凹泛函且对任意的u∈K,有σ(u)≤‖u‖。 因此,Tu∈Kr。 其次,验证对任意 有 且σ(Tu)>a。事实上,常函数 结合式(6),有 综上所述,Leggett-Williams不动点定理的所有假设都满足,因此,T至少有三个不动点,即边值问题(1)至少有三个正解u,v,w满足 ‖u‖ d<‖w‖, (8) (9) (10) (11) ‖u‖ dn<‖w‖,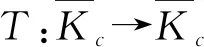
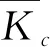
1 预备引理
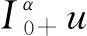
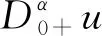

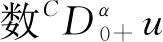
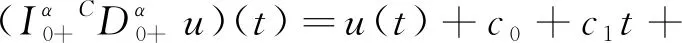
2 主要结果