气泡碰壁反弹的动力学模型研究

于勇，罗松

(北京理工大学 宇航学院，北京，100081)

在化工、石油、制药等很多多相流系统中都存在气泡-气泡以及气泡-壁面的相互作用.这些作用对化学反应、力学特性及传热传质等过程有着重要的影响.因此深入了解气泡的碰撞动力学行为以及建立适当的模型来描述是极其重要的.研究气泡碰撞动力学过程可以为量化凝结、聚集、黏附和破碎等过程提供参考，同时为复杂多相流动系统提供子模型参考.

对于气液变形界面碰撞过程中形成的薄膜及其变化过程的研究具有较长的历史，Tsao等[1]最早用高速相机捕捉到了高雷诺数下的气泡与壁面作用下的反弹现象，实验中发现气泡以终端速度撞击壁面会反弹多次直至黏性耗散掉气泡的动能.但是限于当时的实验条件和方法，气泡碰撞壁面形成的薄膜分布和薄膜排水的动力学过程未能被捕捉到.Legendre[2-3]及Zawala[4]等进行了气泡撞击壁面反弹的实验并从能量的角度量化分析了气泡与壁面撞击过程中的能量变化，其结果表明气泡撞击壁面存在气泡动能和气泡表面能的相互转化，同时发现气泡与壁面的撞击过程由薄膜排水的惯性效应所主导，当惯性力大于粘性耗散力，气泡会发生反弹，反之则不会.Hendrix等[5]采用同步相机和光学干涉方法对毫米级气泡与壁面的碰撞过程进行了实验，实验过程中通过光学干涉法得到了气泡与壁面间的薄膜变化.随后Kosior等[6-7]对表面催化物质以及壁面属性对气泡碰撞行为的影响进行了实验研究.Zhang Xurui及Manica等[8-9]利用集成薄膜测力仪对气泡碰撞过程的受力进行了实验测量，这为一系列模型的验证提供了重要数据.

对于气泡或液滴碰撞过程形成的薄膜排水动力学过程的模型描述吸引了众多的学者.Yiantsios等[10]采用非流动表面条件下的薄膜润滑近似理论得到了浮力作用下小液滴与壁面作用形成的薄膜演化规律，在模型计算中捕捉到了酒窝状的变形.Klaseboer等[11]采用薄膜排水模型和壁面诱导力模型对甲烷液滴与壁面撞击的薄膜排水和反弹过程进行了理论计算，但薄膜分布的准确性未得到验证.Moraga等[12]根据实验数据提出了新的壁面诱导力模型，这一模型中不再求解薄膜润滑理论，而是通过实验数据得到其与浮力和阻力的关系，这一模型显式的引入了Re数、We数和Bo数的影响，是额外薄膜压力模型的改进，但是对理解薄膜排水的详细动力学过程没有帮助，其力的模型误差也较大.Podvin等[13]将Klaseboer的模型扩张到2维来描述气泡与倾斜壁面的碰撞问题.Chan等[14]详细地总结了气泡和液滴的薄膜排水及聚合问题的发展历程，对各种理论模型和动力学边界进行了分析，结果表明Stokes-Reynolds-Young-Laplace模型最能精确地描述气泡碰撞过程中形成的薄膜的演化.随后Manica等[15-16]对不同尺度下的气泡/液滴碰撞过程中的薄膜排水过程以及受力进行了详细的研究，提出的气泡受力模型可以精确地模拟不同尺度下的气泡的反弹轨迹.以上的模型对理解气泡碰撞的动力学过程起到了重要的作用，同时可以为复杂气泡流动系统的直接数值模拟提供了子模型参考[17-19].

综上可知，国外大量学者对于气泡/液滴碰撞的动力学行为进行了研究，实验从开始只能捕捉气泡轨迹到详细捕捉薄膜演化再到可以精确地测量气泡/液滴受力，理论模型可以较为精确地捕捉薄膜变化规律和气泡轨迹.限于作者所知，国内目前暂时无人用此方法研究该问题.本文采用Stokes-Reynolds-Young-Laplace模型和壁面诱导力模型对气泡与固体壁面碰撞的动力学过程进行了分析，讨论了碰撞过程中的薄膜演化规律和膜内压力变化，将计算得到的轨迹与实验结果进行了对比，验证了气泡受力模型的准确性.同时对不同Re数下气泡碰壁过程进行了求解，得到了气泡碰壁反弹规律.

1 数学模型

1.1 气泡受力模型

考虑如图1所示的问题，初始半径为R的气泡或液滴以速度v(t)垂直撞击壁面，考虑为轴对称问题，气泡表面与壁面之间形成薄膜分布h(r,t)，气泡质心距壁面距离为Zd，气泡表面与壁面间形成径向速度分布u，薄膜形成水动力学压强分布p(r,t)，薄膜径向分布的最大位置为rmax.将气泡的运动简化为质点运动，可以得到气泡的受力方程为

(1)

式中：FB为气泡受到的浮力；FD为气泡受到的阻力或拽力；FA为附加质量力；FF为由于气泡撞击壁面界面变形引起的薄膜内润滑压力，又称为壁面诱导力；ρd为气泡的密度.

由于重力的存在气泡上升过程中受到浮力的作用，浮力大小与气泡体积和流体密度有关，

(2)

式中：ρc为周围液体的密度；g为重力加速度.气泡运动过程中由于黏性的存在会受到阻力的作用，阻力为

(3)

式中:μc为周围液体的粘性，Re=2Rρc|v|/μc为气泡运动的瞬时雷诺数.阻力系数CD通过对椭圆形气泡运动的分析计算得到，并经试验验证具有很高的准确性[20].

(4)

(5)

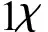
(6)

以上阻力系数的关系适用于变形较大的液滴或气泡(如椭圆形气泡)，对于小气泡或部分液滴，上升运动过程中变形很小，近似为圆形，考虑非滑移气泡表面，其阻力规律与圆球颗粒的阻力规律相似，具有以下关系式.

(7)

当上升气泡处于稳定运动状态时，阻力和浮力平衡，此时气泡的运动速度成为终端速度vT.

气泡从静止加速或与壁面碰撞变速的过程中，由于周围流体的加速或减速会对气泡产生附加质量力.附加质量力为

(8)

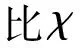
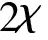
(9)

气泡撞击壁面的模型中最重要部分是气泡和固体表面之间的润滑膜以及控制气泡在该区域变形的表面张力，这种黏性润滑和气泡变形之间的平衡将引起膜内积聚的压力，其大小在特定条件下足以引起气泡反弹.将薄膜内的压力作面积积分可以得到薄膜排水力，又叫壁面诱导力或附加薄膜压力.考虑轴对称薄膜，可得

(10)

式中rmax为薄膜分布的最大径向位置，其中rmax的选取与气泡的变形有关；p为薄膜内的压强分布.除了上述的各种作用力之外，流体的惯性效应还会引起历史力FH，但对于高雷诺数的气泡运动这一力可以忽略.对于薄膜厚度到纳米级的问题或者微纳级的气泡碰撞问题，气泡碰撞壁面的过程中还会有分子范德华力FVDW以及双电层力FEDL.

求解气泡的质心受力方程可以得到气泡质心速度变化v，对速度v积分即可得到气泡的质心位置变化Zd.

1.2 Stokes-Reynolds-Young-Laplace模型

采用合适的模型描述气泡撞击壁面时形成的薄膜演化和膜内压力变化是理解气泡碰撞动力学行为的关键.气泡撞击壁面时，膜内流动满足N-S方程，定义局部薄膜雷诺数Ref(ρcH0v0/μc)，由于分离薄膜厚度H0和气泡表面速度v0很小，有Ref≪1，因此薄膜内流动的惯性效应可以忽略，薄膜内流动可以简化为Stokes流动，则轴对称模型下的N-S方程组可以简化为

(11)

(12)

(13)

式中：u为径向速度分布；v为轴向速度.将连续性方程(11)从z=0积分到h(r,t)，得到薄膜厚度演化的方程为

(14)

在固壁面z=0处，有非滑移边界条件u=v=0，如图2所示，假设气液交界面是不流动界面(immobile interface)，则气泡表面切向的速度分量必定为0，即在z=h(r,t)处，u=0.实际上只有在纯净无杂质的液体中，才会考虑气液交界面为流动界面(mobile interface)，实验表明只要液体中有微量的杂质或表面活性物质就会导致气液交界面为不流动界面.根据式(13)薄膜内压强分布与z向无关，将式(12)对z积分两次，并结合上述速度u的边界条件，可得

(15)

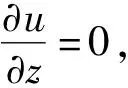
(16)

将式(15)或(16)代入式(14)即可得到描述薄膜演化规律的Stokes-Reynolds方程：

(17)

式中，M=12对应上述详细讨论的非流动界面边界条件(immobile interface)，M=3对应流动界面边界条件(mobile interface).

由于薄膜排水引起的水动力学压力p满足Young-Laplace方程[14]：

(18)

式中σ为表面张力系数，方程(18)是描述薄膜排水动力学行为模型的关键，气泡变形引起的表面能变化是唯一能够储存能量的地方，表面能的变化引起薄膜内压力增加.在气泡撞击壁面反弹的过程中，压力集聚储存的能量会转化为气泡的动能.

当气泡远离壁面时，式(18)中的水动力学压力p为0，因此初始条件的选取需要保证薄膜内的压力分布为0，采用抛物型初始薄膜分布可以满足这一条件，这一分布是半径为R的球形气泡表面的局部近似.因此t=0时的初始条件为

(19)

(20)

式中，H0为t=0时刻r=0位置处的薄膜厚度，选取为气泡受壁面影响可以忽略的初始位置，一般取H0=5R.

对于方程(17)(18)构成的偏微分方程系统，需要4个边界条件.在r=0处，由于是轴对称模型，采用对称边界

(21)

(22)

在薄膜的最外端，此处薄膜近似认为未变形，同时近似有薄膜厚度的变化速度与气泡质心的速度相等，因此有边界条件

(23)

p|r=rmax=0.

(24)

1.3 数值方法

方程(1)(17)(18)及边界条件和初始条件(19)～(24)构成了描述气泡与壁面碰撞过程的动力学模型.将式(18)带入式(17)中可以得到关于薄膜厚度分布变化的4阶非线性偏微分方程.

(25)

该方程没有解析解，即使是考虑弱扰动情形下的解，因此只能采用数值方法求解.采用隐式格式进行求解，对上式中所有关于r的空间导数项采用2阶中心差分格式离散，

(26)

(27)

(28)

(29)

(30)

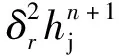
(31)

式中Δt为时间步长.数值差分格式建立后利用已知时刻的h对离散方程中的非线性项进行线性化，最终得到的离散代数方程组的系数矩阵是五对角矩阵，可以通过高斯消去法进行求解.轨迹方程(1)通过4阶龙格库塔法求解.

当建立数值差分格式和数值方法后，整个方程系统的求解步骤如下：通过求解薄膜方程得到薄膜分布h，根据压强方程求得压力分布p，然后通过Simpson 法则求得壁面诱导力FF，求解气泡的轨迹方程得到下一时层的速度v，积分速度得到气泡轨迹Zd，然后根据新的速度v再计算下一时层的薄膜分布，重复以上过程直至计算结束.在每一个时间步的计算内，薄膜厚度的差分代数方程组采用迭代法求解，保证薄膜厚度求解的绝对残差小于10-15，对应的压强分布绝对残差小于10-12.

2 结果分析

2.1 典型气泡碰壁动力学过程分析

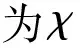
图3显示了气泡运动过程中的受力变化.气泡运动过程中受4个力的作用，即浮力、阻力、附加质量力和壁面诱导力，在不同的运动阶段，各个力对气泡运动的作用不一样.在初始状态时气泡离壁面较远，壁面诱导力不起作用，气泡的阻力和浮力平衡，气泡以终端速度运动，此时气泡无加速度所以附加质量力为0.当气泡靠近壁面时，壁面诱导力急剧增加并对气泡的运动起主导作用，此时气泡的运动主要由壁面诱导力和附加质量力控制，浮力和阻力不再起主导作用.在每一次反弹过后壁面诱导力会出现短暂的负值，此时气泡贴近壁面，有较大的负压区存在.在反弹过后的部分时间里，气泡速度接近0，阻力基本可以忽略，而附加质量力也很小，气泡处于壁面诱导力和浮力的平衡状态.气泡在多次反弹过程中的力的演化规律基本一致.但随着每一次碰撞速度的衰减，壁面诱导力的最大量级逐渐变小.

图4显示了采用不同时间步长计算得到的气泡运动轨迹的对比来验证数值方法的收敛性.从图中可以看出，对于求解理论模型所采用的隐式数值计算方法，采用时间步长10-7就可以得到较好的结果，减小时间步长基本不会引起结果的差异，因此说明了采用的数值算法对时间步长的无关性.图5显示了采用不同空间节点数计算得到的气泡运动轨迹以对比空间网格的收敛性.计算采用的节点数为100，200，400，600，800.从图中可以看出采用不同节点数计算得到的气泡轨迹均趋于一条曲线，差别极小，通过对第1次反弹幅度最大位置处的局部放大图可以看出，除了采用节点数为100的计算结果之外，其余的计算结果均收敛与一条曲线.计算采用节点数200就可以得到很好的结果.

对于采用不用空间节点数计算得到的质心轨迹,可用以下的范数误差分析，

l1error:

(32)

l2error:

(33)

l∞error:

(34)

式中:‖e‖1、‖e‖2和‖e‖∞分别为1范数误差、2范数误差及最大范数误差;NTS即为空间步长数;qt,ref为参考计算结果，一般采用最小网格尺度的计算结果，本文以节点数为800的计算结果作为参考;qt为其余网格节点数计算结果.

当建立起范数误差之后，计算结果关于空间步长的收敛速度可以表示为

(35)

式中：l为网格的细化等级；h为对应等级的空间步长.

表1显示了气泡质心轨迹的范数误差和空间收敛阶数，参考值为节点数为800的计算结果.可以看出，随着空间节点数的增加，计算结果的范数误差逐渐减小，质心位置的收敛阶数也逐步增加，在节点数为200时，接近2，当节点数为600时，大于3.同时可以看出采用不同范数误差计算得到的收敛阶数大小基本相同.

表1 相对范数误差及收敛阶数分析

图6显示了计算得到的气泡运动轨迹，计算分别采用了流动气液界面和非流动气液界面进行计算，结果表明，采用流动界面边界条件下的理论模型得到的气泡轨迹变化与Tsao&Koch实验结果吻合得更好，这说明在他们的实验条件下所研究的气泡表面具有较好的流动性，实际上他们在实验中采用了去离子水，流动系统比较纯净.其中理论模型得到的结果对于反弹运动的最大幅度的预测略小于实验值，最大误差在气泡反弹的最大位置处，最大误差在10%以内，同时可以看出计算得到的气泡质心随时间变化的曲线与试验结果相比存在时间上的相移现象.这是由于实际中的气泡在碰撞和反弹过程中处于持续的变形之中，在碰撞过程中保持变形较大的椭球形形状，而反弹回去之后会逐渐恢复为球形，实际上变形会引起阻力系数和附加质量力系数的变化.而在理论模型之中，阻力系数和附加质量力系数都保持为常数，因此引入误差以及速度随时间演化上的差异，这是理论模型进一步修正的方向，但是可以看出这里引入的误差对于气泡反弹运动的描述影响不大.同时可以看出，采用非流动界面边界条件得到的气泡反弹后的最大幅度更小，气泡动能衰减的更快，第2次和第3次反弹幅度急剧变小.这是由于采用非流动界面边界条件引起的气泡变形和粘性耗散会更大.图中展示了Moraga等[12]的计算结果来进行了对比，可以看出，本文计算结果与Moraga计算结果基本一致，但Moraga计算结果的相移现象更加明显.

图7显示了模型预测得到的气泡质心速度变化，气泡在最接近壁面和反弹后离壁面最远时速度为0，根据不同的速度方向变化可以将气泡运动过程分为不同的碰撞和反弹过程.可以看出在每一次碰撞和反弹过程中气泡的最大运动速度在变小，而且气泡从接近壁面速度最大到远离壁面速度最大的运动阶段里速度变化更快，此时壁面诱导力FF对气泡的运动起主导作用.再观察速度气泡轨迹和速度的衰减，可以发现其类似于阻尼振荡衰减，但实际上的能量耗散小于采用黏性阻尼振荡器来分析这一系统时的能量耗散，气泡反弹的幅度也大于采用黏性阻尼振荡器来分析得到的反弹幅度.这是由于气泡变形的存在，使得能量转化为气泡表面能，表面能可以再转化为气泡的动能，这使得实际的黏性耗散小于黏性阻尼振荡器的耗散.

气泡在碰撞壁面的过程中会发生变形，接近壁面的表面变形程度较大，在气泡速度为0时，气泡质心距离壁面最近，薄膜变形达到最大，随后气泡反弹气泡形状恢复.此处详细讨论气泡前两次碰撞回弹过程中的薄膜剖面分布变化，来展示气泡撞壁的动力学过程.图8显示了气泡第1次碰撞壁面时薄膜的变化规律，从图中可以看出气泡中心处的薄膜厚度变化率先大于边缘处的薄膜厚度变化率，随后基本不变，气泡由初始近似球形形状发展出酒窝状的形状，酒窝状出现在气泡中心和边缘的中间部位.图9显示了气泡第1次反弹过程中的薄膜剖面变化.从图中可以看出，气泡在反弹时，酒窝状的位置朝气泡中心位置发展，此时气泡中心处薄膜厚度基本不变，但在部分时刻仍然朝壁面贴近，后面可以看到这是受到局部负压吸力作用的影响.当酒窝状凸起发展至中心位置后，气泡迅速回弹，恢复至近似初始形状.

图10显示了第2次碰撞过程中的薄膜剖面演化.薄膜仍然形成了酒窝状的分布，但此时酒窝状出现的位置离气泡中心更近，酒窝状形态更加明显.此时气泡撞击壁面的速度变小，这说明气泡撞击壁面的速度对薄膜的变化是有影响的，特别是对酒窝状的形成和分布.图11显示了第2次反弹过程中的薄膜变化.与第1次反弹过程一样，酒窝状的位置会超气泡中心位置发展，部分时刻薄膜中心处的位置仍受负压影响向壁面靠近.

图12显示了薄膜中心处的厚度变化h0(t)和最小薄膜厚度hm(t)随时间的变化规律.从图中可以看出，在远离壁面时，两者相等，此时气泡的最小薄膜位置出现在中心处，未有酒窝状出现.在气泡最接近壁面时刻(速度为0)附近，最小薄膜厚度小于薄膜中心位置的薄膜厚度，此时预示着酒窝状的出现，薄膜润滑效应起到主导作用.同时此气泡初始动能大，会反弹多次，可以看出在计算内的4次反弹过程中均有酒窝状的形状出现.实际上酒窝状形状的出现受薄膜内部排水过程和气泡变形的影响.对于气泡和液滴等的碰撞动力学行为中形成的薄膜中均会存在酒窝状、涟漪状、丘疹状的表面形态分布.这些形状的存在会使得薄膜内部形成非等截面的流动通道进行薄膜排水过程，引起薄膜内流动的变化.

图13和图14分别显示了第1次碰撞和反弹过程中薄膜内压强的变化规律.在气泡接近壁面过程中，气泡初始压强分布为0，随着气泡的变形，中心位置压强迅速上升随后保持不变，压强沿径向递减.其中最大压强接近200 Pa，此气泡的Laplace压强2σ/R=187.34 Pa，最大压强会大于球形气泡所具有的Laplace压强，压强分布引起气泡撞击壁面时的局部变形.在气泡远离壁面反弹的过程中，最大压强数值有所增加，压强随径向加速衰减的位置向薄膜中心发展，同时，在酒窝状出现的位置及其外部会出现局部的负压区，负压区的位置随酒窝状的位置向薄膜中心发展.当酒窝状完全发展至中心处时，会形成完全的反压区.这些反压的存在会使壁面诱导力在部分时刻反向.当气泡反弹恢复至近似初始形状时，压力分布衰减为0.

图15和图16显示了第2次碰撞和反弹过程中薄膜内压强的变化情况.可以看出，第2次碰撞和反弹过程的压强变化规律与第1次相同，只是压强加速衰减的位置与酒窝状位置一样向薄膜中心处发展.最大压强的量级与第1次相似.

2.2 酒窝状变形的形成和气泡反弹规律

以上讨论了典型高雷诺数下气泡碰壁过程中的薄膜变形和膜内流体动压强变化.实际上，对于水中变形气泡而言，其与壁面碰撞过程中的薄膜变形与膜内压强分布规律与以上相同，只是酒窝状变形形成的位置不一样.酒窝状变形形成时的液膜厚度决定了薄膜排水的时间，准确地预测酒窝状变形形成时的薄膜厚度和薄膜排水时间对于研究气胶体颗粒碰撞时的稳定性有重要意义.酒窝状变形处的薄膜厚度最小，当薄膜不稳定时，薄膜的破碎会最先从这里开始.记气泡与壁面碰撞过程中酒窝状第1次形成时的薄膜厚度为hD，此时气泡靠近壁面界面为扁平形，中心位置及周围位置液膜厚度相等.考虑气泡界面为非流动界面时，对于以恒定速度撞击壁面的气泡这一厚度可以通过理论分析得到[21]，其表达式为

(36)

对于不同尺寸的气泡碰壁问题，气泡具有不同的终端速度以及不同的雷诺数.气泡在碰壁的过程中动能会逐渐被耗散，当动能被完全耗散掉时，气泡将不再反弹.图10显示了不同(We,Re)控制下的气泡反弹次数机制图，其中韦伯数We=2ρv2R/σ.这里规定气泡碰撞壁面后质心反向运动的最大幅度超过气泡半径的1/10时认为气泡发生反弹.从图中可以看出，气泡反弹次数随着雷诺数的增加而增多.在雷诺数Re约大于29时，气泡会发生反弹，反之气泡不发生反弹；当雷诺数Re约大于90时，气泡反弹次数增加为两次；当Re约大于190时，气泡反弹次数增加为3次；当雷诺数Re约大于310时，气泡的反弹次数增加至4次；当Re约大于430时，气泡的反弹次数增加至5次；当Re约大于586时，气泡反弹次数增加至6次，在现有的计算中气泡出现的最大反弹次数为6次.

3 结 论

采用壁面诱导力模型和SRYL模型对气泡碰壁反弹过程进行了求解和分析，得到了以下结论.

① 随着气泡尺寸及雷诺数的增大，气泡在与壁面作用的过程中会反弹0到多次，基于壁面诱导力的气泡轨迹模型可以很好地预测气泡的反弹规律.高雷诺数的气泡会反弹多次直至动能被全部耗散.

② 上升气泡碰壁过程中受到浮力、阻力、附加质量力和壁面诱导力.在气泡接近壁面的过程中，壁面诱导力急剧变化并对气泡运动起主导作用，壁面诱导力是引起气泡反弹的最主要因素.

③ 气泡在最接近壁面时，气泡表面靠近壁面的部分会呈现丰富的变形，存在类似于薄膜润滑效应的动力学行为.薄膜出现酒窝状的形状，膜内压强也会因为薄膜变形和排水过程而发生变化，压强的最大值会大于Laplace压强.

④ SRYL模型对气泡碰撞壁面的薄膜排水动力学过程做出了较为详细的描述和解释，可以为复杂两相流动的数值模拟提供子模型参考.