无线传感器网络中传感器节点定位的递归加权最小二乘优化方法

塞拉斯, 许皓, 宋扬, 孙华飞

(1.北京理工大学 数学与统计学院, 北京 100081；2.西华师范大学 数学与信息学院, 四川，南充 637002)

无线传感器网络已被广泛认为是绿色建筑通信最新发展中的一项有很好前景的技术.目标定位问题是无线传感器网络实现的基本问题之一.依靠定位技术中的到达角、接收信号强度(RSS)或时间延迟信息可用于确定目标节点的位置[1-7].近年来, 基于能量的定位方法因其成本低、实施简单而备受关注[8-13].本文采用最小二乘优化算法, 研究了基于接收信号强度测量的信号源定位问题.首先, 采用对数距离传播损耗模型, 通过路径损耗测量, 建立了基于接收信号强度的测量噪声模型.然后, 利用UT变换给出了一种线性化形式.最后, 通过最小化损耗函数得到线性最小二乘解和加权最小二乘解, 进而提出了递归加权最小二乘法.大量的模拟仿真实验结果表明, 本文提出的迭代加权最小二乘解在定位精度方面比已有的LLS算法、WLS算法[9]和RLS算法[11]有更好的表现.

1 路径损耗模型的线性化

考虑一个由m个传感器节点组成的网络, 这些节点分布在二维区域2中.并且设这些锚节点的坐标为pi=[xiyi]T,i=1,2,…,m.设目标节点pt=[xtyt]T∈2发射以PT为功率的无线电信号，那么目标节点到第i个锚节点的路径损耗量为

Li=PT-Ri，

式中Ri为第i个锚节点的RSS量.

文献[11]中提到, 路径损失量Li可以由如下对数距离传播损失模型给出

Li=:PL(di)+Wi=PL0+10hilg(di/d0)+Wi，

(1)

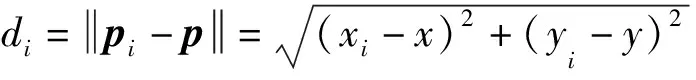
对式(1)两边同除10hi, 并重写为

(2)

zi=10yi，

(3)

(4)

(5)

式中：

(6)

(7)

均为常数.于是, 式(4)可以写为

(8)

选取第r个锚节点作为参考锚节点, 则

(9)

线性化模型为

b=Ap+w，

(10)

式中b为观测向量，

(11)

此外, 系数矩阵

(12)

w=[w1rw2r…wnr]T为噪声向量,wir为0均值高斯白噪声.

wir的方差和协方差矩阵分别为

(13)

(14)

从而, 求解式(10)的线性最小二乘(LLS)的解归为最小化目标函数

fL(p)=(b-Ap)T(b-Ap)，

(15)

得到的解为

2 递归加权最小二乘算法

观察到式(15)得到的解没有考虑到噪声的方差、协方差.如果这些信息已知, 可以对每个测量赋予权重, 这会对定位结果的精度起到有效的作用.因此, 利用协方差矩阵中的信息, 本文提出了递归加权最小二乘法(RWLS).

对于一个给定的协方差矩阵C(p), 求解式(10)的加权线性最小二乘的解归为最小化目标函数

fRW(p)=(b-Ap)TC(p)-1(b-Ap)，

(16)

(17)

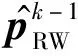
(18)

3 模拟仿真

为了检验所提出的RWLS方法的性能, 在每次实验中, 先在50 m×50 m区域内随机取服从均匀分布的m个锚节点和20个目标节点.设式(1)中的PL0=35 dB.为简单起见, 噪声标准偏差和路径损耗指数分别在不同节点处取相同的值, 即σi=σr=σ及hi=hr=2.2.采用均方根误差作为定位估计误差, 算法中的阈值取ε=0.01.所有的模拟结果平均超过200次试验.

3.1 定位结果分析

在这一小节中给出了定位结果, 并对不同的锚节点个数m和噪声方差σ2进行了详细的分析.图1展示了RWLS法对不同的锚节点个数m和噪声方差σ2的效果.可以看到随着锚节点个数m的增加,定位精度越大, 即均方根误差越小；噪声方差越大, 精度越小, 即均方根误差越小.

3.2 与已有算法的比较结果

在本小节模拟中, 主要将提出的算法(RWLS算法)与基于RSS的2种定位算法进行了比较：① 文献[9]提出的加权最小二乘法(WLS算法)；② 文献[11]提出的基于递推最小二乘优化的定位方法(RLS算法).

在以下2种情况：① 噪声方差σ2=2,不同锚节点数量；② 目标节点个数N=10,不同噪声方差σ2,通过模拟仿真, 分别对LLS法、RLS法、WLS法和RWLS法的定位精度进行了比较, 如图2，图3所示.结果说明RWLS法比LLS法、RLS法和WLS法有更高的精度.

4 结 论

提出了一种基于接收信号强度的无线传感器位置估计的递推加权最小二乘优化方法(RWLS法).首先将非线性路径损耗模型转化为线性方程组, 并进行UT变换.然后构造了一种基于线性最小二乘法的低复杂度传感器节点定位算法.在考虑方差矩阵的情况下, 给出了线性最小二乘法初始解的递推加权最小二乘法.仿真实验结果说明了该算法的良好性能.