基于广义卡尔曼-布西滤波的压缩光相位自适应估计方法

陈树新，徐涵，吴昊，房亮，崔军辉，钟慧

(1.空军工程大学 信息与导航学院，陕西，西安 710077；2.空军工程大学 研究生院，陕西，西安 710077；3.94969部队，上海 200436; 4.95655部队，四川，成都 611530)

量子参数估计[1]是在量子系统中对经典变量的估计问题，其中量子相位估计已经成为量子通信[2-3]、量子定位[4]和引力波探测[5-6]等领域的理论基础，受到了广泛的关注.导航系统中的相位式测角同样需要精确的相位参数[7]，而利用量子理论获取相位参数的导航机制可以克服散粒噪声的影响，有望提高导航定位的精度.

上述的压缩光相位估计方法能够实现的关键在于如何调整本振相位，以减小真空起伏对零拍电流的影响.但是他们均采用了数据平滑方法获取相位信息，这对实时性要求较高的导航系统来说并不适用.为此，本文在利用量子零拍探测测量相位压缩光的相位时，基于广义卡尔曼-布西滤波[17-18](extended Kalman-Bucy filter, EKBF)设计了零拍锁相环，所设计锁相环能够对本振相位进行实时反馈控制，保证其与待测信号相位正交，同时提高了一阶泰勒展开的精度，从而得到精度最高的压缩光相位.通过求解李雅普诺夫方程得到了估计误差与各参数间的关系，理论分析和仿真结果表明此方法可以实现压缩光相位的精确估计，精度能够突破标准量子极限.在最优压缩度下能够得到最高的估计精度，且最优压缩度越高，相位估计精度越高.

1 系统模型

首先在状态空间中定义状态模型和量测模型，相位压缩光的调制相位模型φ(t)为Ornstein-Uhlenbeck(OU)过程[19]

(1)

式中：λ-1>0为φ(t)的相关时间；κ>0决定相位变化的大小；v(t)为具有统一振幅的均值为0的高斯白噪声，满足E[v(t)v(τ)]=Nδ(t-τ).

用零拍探测测量由上述相位模型调制后的相位压缩光，将本振相位Φ(t)通过反馈控制为Φ(t)≈π/2+φ(t)，然而φ(t)是未知的，因此需要利用最优估计理论得到φ(t)的最优估计值φ(t)，从而得到零拍探测输出电流

(2)

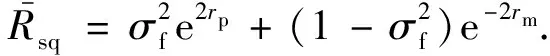
(3)

设探测中总损耗l，相位压缩度与反压缩度分别为R-=e-2rm和R+=e2rp，压缩度和反压缩度可以由统一压缩参数r和探测总损耗l表示为[12]

(4)

2 零拍锁相环设计

2.1 广义卡尔曼-布西滤波算法

假设连续非线性系统模型为

(5)

式中：f[·]和h[·]都是或者其中一个是关于自变量X(t)的非线性函数；w(t)和v(t)为高斯白噪声.

针对此类连续非线性系统而言，卡尔曼-布西滤波的基本方程并不适用，因此需要利用将非线性滤波算法广义卡尔曼-布西滤波.现定义连续系统的真实轨迹与最优状态估计轨迹偏差为

(6)

(7)

同理

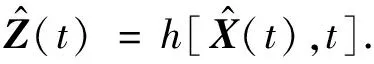
当δX(t)足够小时，非线性式(5)可以在最优估计附近进行泰勒展开，并取其一次近似值，得

(8)

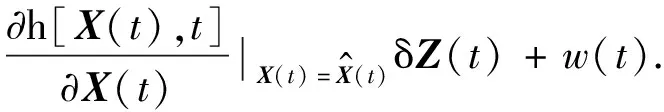
(9)

将式(7)带入式(8)(9)可得到

(10)

δZ(t)=H(t)δX(t)+w(t).

(11)

不同于卡尔曼-布西滤波，转移矩阵F和H的获取需要求雅可比矩阵，分别为

(12)

(13)

得到转移矩阵F和H后，利用卡尔曼-布西滤波的基本方程推导广义卡尔曼-布西滤波，卡尔曼-布西滤波的基本方程为

(14)

K(t)=P(t)HT(t)γ-1(t)，

(15)

P(t)HT(t)γ-1(t)H(t)P(t)+

G(t)q(t)GT(t)，

(16)

式中：K(t)为卡尔曼增益；P(t)为协方差阵.将式(12)和(13)带入卡尔曼-布西滤波基本方程，得到广义卡尔曼-布西滤波方程如下

(17)

(18)

(19)

2.2 基于EKBF的零拍锁相环设计

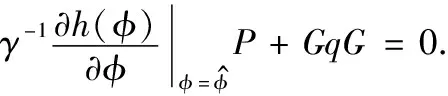
(20)

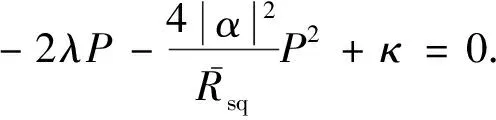
(21)

求解式(21)可得

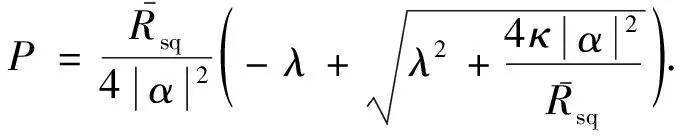
(22)

由式(17)与(18)可得相位预测方程以及卡尔曼增益为

(23)

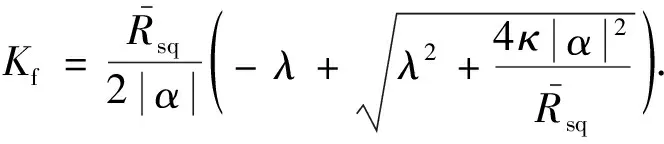
(24)

将式(2)线性化可得

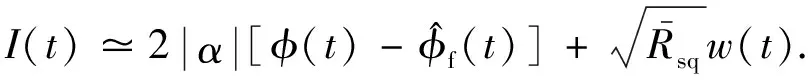
(25)

将式(25)进行等价变换可以将量测模型改为

(26)

将式(26)带入式(23)化简得

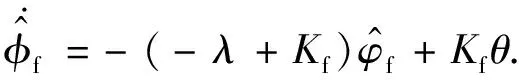
(27)

由式(27)可得到传递函数

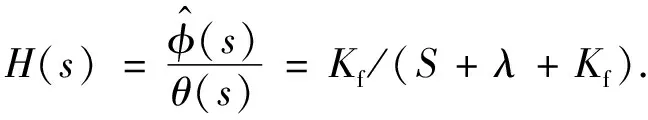
(28)

由式(24)～(28)可以得到基于广义卡尔曼-布西滤波的零拍锁相环如图2所示.

在利用零拍探测对相位压缩光进行测量时，需要本振相位与信号场相位正交，才能最大程度地克服散粒噪声的影响，同时也能提高一阶泰勒展开的精度，所设计锁相环是把量测结果(这里的量测特指式(26))通过传递函数为H(s)的滤波器，然后将所得结果进行拉普拉斯反变换，得到状态估计值，最后根据估计相位调整本振相位的值.以此循环，确保每一时刻测得的零拍电流受到最小的散粒噪声影响，从而得到相位压缩光的相位估计值.

3 误差分析及对比

3.1 误差分析

利用李雅普诺夫方法对所提方法进行误差分析，在构造李雅普诺夫方程时，首先建立如下状态空间模型

(29)

式中：

由此可以得到李雅普诺夫方程

APs+PsAT+BBT=0

(30)

式中：稳态状态协方差矩阵Ps为对称矩阵，设为如下形式

(31)

求解式(30)可得

(32)

相位估计误差可表示为

(33)

由此得到均方根误差

(34)

3.2 仿真结果与分析

由式(34)可知均方根误差与各个参数的关系，为了更加直观观察参数之间的联系，得到相应的结论，本文采取仿真的方式对估计精度与各参数间的关系进行讨论.参数设置[12]如表1所示.

表1 参数设置

3.2.1实验一：均方根误差与压缩度的关系

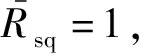
3.2.2实验二：均方根误差和相位压缩光幅度平方的关系

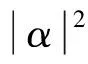
3.2.3实验三：最优压缩度与各参数间的关系

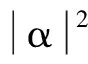
4 结 论

利用非经典光源-压缩光获取相位参数，可以克服散粒噪声的影响，进一步提高导航系统的定位精度.由于导航系统的非线性特点以及对实时性要求较高，传统的线性化平滑估计方法并不能用来获取导航系统中的相位参数.为此，本文基于EKBF算法设计了零拍锁相环，对本振相位进行实时控制，实现了对压缩光相位的估计，并利用李亚普诺夫方法对该方法进行了误差分析.仿真结果表明：① 压缩光可以克服散粒噪声的影响，突破标准量子极限，能够有效提高导航系统中的定位精度；② 在最优压缩参数下才能得到最小的估计误差，且最优压缩度越大，估计误差越小.下一步，将继续利用非经典光源对具有高非线性特点的导航测角相位模型进行跟踪，由此实现精度更高的目标跟踪定位.