基于CT扫描图像的砂岩石三维建模研究

黄贤胜，成卫青，林 伟，熊生春

(1.南京邮电大学 计算机学院，江苏 南京 210023;2.中国科学院 渗流流体力学研究所，河北 廊坊 065007)

0 引 言

随着CT扫描技术和各专业学科的发展，在物质探测方面所具有的巨大优势使得CT技术在非医学领域(如工业、地球物理、工程、农业、安全监测、油气勘探等)得到了广泛的应用[1]。文中利用CT扫描技术对砂岩石岩心进行切片扫描，得到二维CT序列图像。

计算机进行建模的目的是通过一系列二维图像构造出一个简单直观的模型，这个模型能反映真实世界中具体存在的物体，是真实对象的“数学数据抽象”。在石油地质研究领域，对岩石的切片进行分析解读是很有必要的。通过计算机技术可以对岩石薄片图像进行分析处理，快速准确地获取岩石样品参数：如孔隙度、孔隙形状、孔喉比和吼道配位数等特征信息。基于上述二维图像中采集的特征信息，可以将其拓展到三维空间[2]。利用计算机进行三维岩心建模与可视化技术已经存在并且发展了好几十年，目前的三维建模和可视化主要有两个作用：一个是利用解析出的数据构建出三维模型，另一个是对地底石油层是否可勘探提供理论基础。

岩石(多孔介质)三维重构和可视化的重要意义主要表现在以下几个方面：(1)传统的以实验为主要研究方法的方式已经满足不了某些问题的基本需求，如低孔渗储层的岩心渗透问题、复杂储层的岩石物理属性问题[3]。(2)重构出的孔隙网络结构可以用于更好地分析整个岩石的拓扑结构和几何特征。多孔介质内部结构复杂多样，主要由孔隙空间和骨架组成，其中孔隙空间又分为大孔隙和喉道，大孔隙代表较大的孔隙空间，喉道代表相对狭长的孔隙空间。

1 研究现状

1.1 主要方法

目前，国内外实现岩心建模和可视化的技术主要包括以下几种：

(1)直接在已有的三维建模软件上进行操作。比较常用的软件如Blender、UG、Seamless 3d、3d Canvas等；也可以在软件上对已经建好的模型进行再加工再改造，满足相关的需求。这种方法比较简单易上手，不需要考虑复杂的结构、对应的节点坐标和采用的算法等，直接将数据输入进去，就能得到想要的重构模型[4]。

(2)在现有的系统中，运用相关的编程语言加上可视化工具也可以实现三维建模的操作。比如OpenGL，与平台无关，可以在任何的软件系统中实现三维建模可视化[5]，但是这类方法可操作性差，对专业知识要求高，工作量比较大，所以并没有得到广泛的应用。

(3)利用VTK进行三维重构。在VTK中可以自由获取它的源码，世界上大量的研究人员都是使用VTK库进行3D图像建模和可视化操作。

文中采用VTK和C++语言相结合的方法，直接调用VTK中封装的MarchingCubes类—vtkMarchingCubes类进行三维建模，实现岩心的三维可视化功能。通过对孔隙和骨架进行分割，分析了孔喉结构，立体地展示岩心内部的空间结构。

1.2 VTK简介

VTK(visualization toolkit)是一个开源的免费软件系统，它包含了一个C++类库和众多的接口层，可运用在建筑学、气象学、医学、生物学或者航空航天学上，通过对体、面、光源等的逼真渲染，帮助人们理解那些采取错综复杂而又往往规模庞大的数字呈现形式的科学概念或结果。它具有强大的三维图形功能，在极大地改善可视化效果的同时又可以充分利用现有的图形库和图形硬件[6]。

1.3 STL文件简介

STL文件类型是3D SYSTEM公司在1988年编订的接口协议，是专门为快速原型制造技术服务的三维图形文件格式。STL文件有2种类型：ASCII格式和二进制格式。STL文件由多个三角形面片的定义组成，每个三角形面片的定义包括三角形各个顶点的三维坐标及三角形面片的法矢量[7]，这些三角面片的法向量均要求指向实体外部的方向，同时模型表面必须布满三角面片，不允许有遗漏(裂缝和空洞)[8]。

ASCII格式的STL文件的基本结构[9]如下：

solid filename //STL文件路径及文件名

facet normal x y z //三角面片法向量的3个分量值

outer loop

vertex x y z //三角面片第一个顶点坐标

vertex x y z //第二个顶点坐标

vertex x y z

End loop

End facet //第一个三角面片定义结束

……

End solid filename //整个STL文件定义结束

2 MarchingCubes简介

2.1 三维可视化的理解

近年来，随着计算机运算能力的不断加强和设备的不断改进，研究人员提出了基于体素的体绘制实现[10]。但是面绘制仍然是进行三维可视化的主流操作，面绘制是通过先建立网络模型之后再进行渲染的方式完成三维模型构建。

2.2 MarchingCubes基本原理

MarchingCubes (MC)算法是面绘制算法中的经典算法，而且简单容易实现，得到了广泛的应用。

首先在MC算法中要明确一个叫做“体素”的概念。体素是在三维图像中由相邻的八个体素点(三维数据场中相邻两层中相邻的八个顶点)组成的立方体，八个体素点构成一个体素，对体素中的每一个体素点进行编号[11]，图1表示其基本结构。

图1 立方体体素基本结构

MC算法的主要思想是通过在体素中构建出各种不同的三角面片。大量的三角面片构成了一个等值面(isosurface extraction)，这个等值面就是重建模型的表面。等值面上的点定义如下：

{(x,y,z)|f(x,y,z)=c}

其中，(x,y,z)为空间点的坐标，f(x,y,z)为对应点数据的值，常数c为三维重构过程中给定的阈值。

2.3 MC算法的步骤

(1)确定体素中等值面的剖分方式。

判断体素中的顶点状态，某个顶点的值是大于或者等于给定阈值时，该顶点就被标记为“1”，反之该点的状态就标记为“0”。在整个数据场中，在每个体素内重构一等值面片，将得到的所有近似等值面片拼合起来，故称之为“移动立方体”法[12]。

因为每个顶点每次有“0”或“1”两种情况，所以总共就有28(256)种三角剖分状态。根据对称性和旋转对称性，可以把256种最终简化细分成15种。

为了确定每个体素是对应于哪种构型，在程序中加入了一个字节长参数——构型索引index指数。该index指数每字位分别表示体素八个顶点的状态值，如图2所示。

图2 索引index字节

对于图1这一基本构型，用序列来表示其三角剖分形式：{3,11,2，-1，-1，-1，-1，-1，-1，-1，-1，-1，-1，-1，-1，-1}，此序列表示的是第3条边、第11条边和第2条边上有三角面片的顶点，-1表示缺省。

(2)计算等值面顶点处的坐标。

当体素内三角面片剖分方式确定后，由于MC算法假设棱边的像素值是呈线性变化的，所以在体素上两个端点的状态分别为“0”和“1”的边上，必有一点等于阈值(等值面的值)，此点也就是三角面片的顶点。计算该边上等值面的顶点和该顶点的法向量。对于体素某一棱边，设其两个端点(P1、P2)的标量数据为V1、V2，那么插值得到的交点(即三角面片的顶点)为P，P的求解表达式为：

P=P1+(isovalue-V1)(P2-P1)/(V2-V1)

其中，P为顶点坐标，P1、P2为两个端点的坐标，V1、V2为两个端点处的像素值，isovalue为等值面的值。

(3)计算等值面顶点处的法向量。

要把等值面绘制出来，还需要计算三角面片的法向量。利用中心差分法计算出体素中各顶点处的梯度，再利用线性插值法求出三角面片各顶点的梯度(法向量)，实现等值面的绘制[12]。

设立方体顶点处的法向量为N1、N2(标量数据仍然为V1、V2)，利用线性插值得到的三角面片顶点处法向量为：

N'=N1+(isovalue-V1)(N2-N1)/(V2-V1)

(4)引入邻接表。

结合相关文献可知，在实际的三维建模中，有一部分体素并不需要去遍历，是可以直接忽略的。文中采用对邻面延伸的方法，这样建模的效率又得到了提高。确定了一个立方体的所有三角面片后，可根据三角面与立方体各面相交的情况，仅遍历相关的邻接立方体[13]。为此，可以先构建一个邻接表分别存储256种立方体的三角面片构建应延伸的方向(前、后、上、下、左、右)。

3 三维建模的改进

3.1 岩心二维图像预处理

3.1.1 去虚边

本次实验的数据集是对致密砂岩岩心进行CT扫描得到的二维图像。由于岩石扫描图像存在亮度较亮或较暗、对比度不明显、图片画面模糊等缺陷，严重影响图像建模的准确性。因此，在不损坏图像有用信息的前提下需要对其进行适当的去噪声、去虚边等操作。

(1)获取阈值。

高斯滤波器是一种线性滤波器，能够有效地抑制噪声和平滑图像。首先，将原图像进行颜色空间转换，转换成灰度图，然后利用高斯滤波器函数进行滤波操作，将灰度图与指定的高斯内核进行卷积运算。最后创建滚动条(createTrackbar)函数，以及对图像取不同阈值进行二值化处理的函数，通过手动控制滚动条的方式，调整二值化的阈值，直观观察出合适的阈值大小。在CT高分辨率切片原图中选取240.tif、282.tif和330.tif，经过不断调整后，确定这三张图像的阈值分别为174、170和167，生成的二值化图像分别如图3(a)、(b)和(c)所示。

(2)形态学处理。

运用形态学中的膨胀和腐蚀操作。膨胀(dilate)就是求局部最大值的操作，使图像部分区域亮度增加。与膨胀相反，腐蚀(erode)就是求局部最小值的操作。腐蚀可以简单理解为消除物体所有边界点的过程，使整体更暗。特别是在黑白交界的地方，膨胀和腐蚀的现象会非常直观明显。

为去除原图中的虚边(发白模糊区域)，膨胀会使白色区域膨胀，腐蚀会减少白色区域。先腐蚀，让黑色区域中的一些白色像素点消失，同时白色区域块也会暗一些，再通过膨胀补回来是进行开运算的过程；先膨胀会将一些散落的白色小块通过扩增连接到一起，再腐蚀削减一点是进行闭运算的过程。灵活运用开运算和闭运算，膨胀和腐蚀不同的次数，会产生不同的效果。对之前的三张CT原图进行形态学操作，使用的阈值范围是合适阈值X到255，并进行了抠图和找轮廓操作。实际的操作分别是：

①切片240.tif经反复试验后依次使用了腐蚀一次和膨胀三次，使用的阈值范围是174到255，生成图3(d)；

②切片282.tif经反复试验后依次使用了腐蚀一次和膨胀四次，使用的阈值范围是170到255，生成图3(e)；

③切片330.tif经反复试验后依次使用了膨胀两次和腐蚀一次，使用的阈值范围是167到255，生成图3(f)。

图3 去虚边和形态学预处理结果

3.1.2 分层灰度化和裁剪

分层灰度化是一个分割过程，分割可以将感兴趣部位提取并显示出来，便于对模型重建进行判断[8]。将背景的灰度值从原来的0(全黑)变成128，再对岩心内部进行二值化操作。明显地观察出黑色部分是孔隙，不规则地分布在白色的骨架中。这时的二维切片图片就转换成了灰度128的背景、灰度255的骨架和灰度0的孔隙。

由于文中的CT扫描图像是2 048*2 048的tif格式的图片，一张图片所占内存就高达4 M，所以要想完成大量tif格式图片的建模就需要进行裁剪。利用Matlab裁剪工具裁去的是背景部分，保留岩心部分。图4显示已去虚边的240.tif图像及其灰度化与裁剪结果。

图4 切片240.tif去虚边、分层灰度化与裁剪结果

3.2 对移动立方体算法(MC算法)的改进

(1)三角面片顶点计算优化。

根据前面介绍的传统MC算法，如果使用线性插值法直接计算三角面片的顶点(等值点)和对应的法向量，那么过程会很复杂，运算量巨大，同时也会消耗大量的运算时间，而且如果体素量过大，数据场数据量更高，则生成的三角面片和真实的三角面片就有较大的出入。为了降低算法运行时间，有人提出使用黄金分割点作为该边的等值点[14]，由于每个体素都很小，确定每个体素每条边的黄金分割点仍需要经过一些计算，效率上值得再次商榷。文中采取的方式是将体素边分为四等份，提取四等分点，该边的四分之一处的点即为三角面片的顶点，计算上简单方便，极大减少了计算量，同时产生的三角面片比较准确。

(2)顶点法向量计算优化。

法向量也能进一步的简化，法向量计算改为对体素棱边上的顶点的法向量直接求平均，具有很好的效果。

经过一系列的改进后，伪代码如下：

输入：预处理后的二维图像

输出：三维模型

Begin：

1.初始化二元标志数组List={Flag，p}，Flag表示立方体p是否被访问过，初始化CubeQueue队列(利用存放待处理的立方体)，初始化存储256种立方体的邻接关系的邻接表neiborCases；

2.然后检测数据集，选取一个构型索引index不为0或255的立方体作为p，并将其压入队列CubeQueue中，并置List[p].Flag=0；

while(!CubeQueue.empty()){

3.从CubeQueue中取出队首立方体C； //编号C的立方体

4.if(List[C].Flag==1) continue； //表示该编号的立方体已经处理过

5.令List[C].Flag=1；

6.根据当前立方体体素的顶点状态得到其构型索引index；

7.利用构型索引index值查找三角剖分表得到当前体素的剖分形式，结合文中所述的计算方法求出面片的顶点坐标和顶点处的法向量，并将其作为输出的数据；

8.通过index查找neiborCases邻接表，将邻接的立方体压入到CubeQueue队列中去；

9.用VTK工具绘制三维模型}

End

4 实验结果与分析

文中实验使用的主机有8G RAM，操作系统为64位 Windows 7。开发使用Cmake，Visual Studio 2013嵌入VTK类库、Python-opencv图像处理函数库和Pycharm 2018编辑器。使用VC++、Python和Matlab语言编程实现所有功能。

(1)模型对比。

对100张预处理后的二维图像进行三维建模，结果如图5所示，前两张图是经典MC算法生成的模型，后两张是改进MC算法生成的模型。

图5 改进前后算法重构模型

(2)3D实物打印。

在3D打印机上读取文中生成的STL文件，采用9 400树脂材料进行打印，精确的尺寸为89.253 mm*81.139 mm*49.750 mm。图6是打印出的实物模型。

图6 致密砂岩岩心放大3D打印实物

(3)实验结果总结。

由于建模的图片数量有限，而且新旧算法都是对岩心进行建模，都有较高的精度，所以改进前后的整体模型相异性较小。改进后的岩心内部的孔隙都能较好地重构出来，能够保证建模的准确性。表1是多次实验结果的汇总。

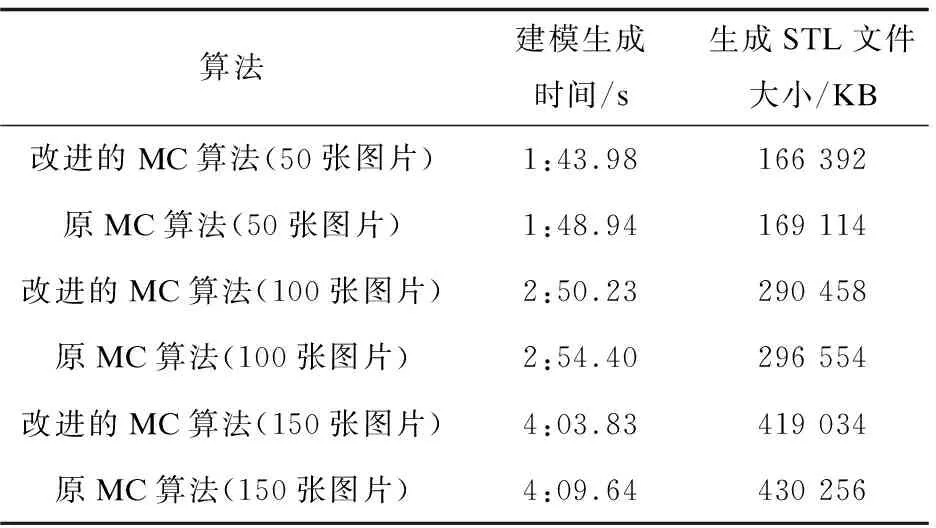
表1 改进的MC算法和原始的MC算法的对比

由表1可见，改进后的MC算法无论从建模的运算时间上还是生成STL文件的大小上，都有不同程度的优化，提高了效率。在保证生成模型准确性的基础上，缩短了运算时间，减小了最终文件大小，有一定的优势，增强了MC算法绘制的实用性。

5 结束语

针对岩心的CT图像设计了有效的图像预处理方法，对传统建模方法MC进行了改进，并利用VTK编程实现了一个对二维CT图像序列进行三维建模的系统。实验结果表明改进MC算法在保证生成模型准确性的基础上提高了三维建模的效率。