人教版与北师版初中数学教材对比研究

吴限　刘素红

摘要：数学是一门研究数量关系和空间形式的科学，几何在数学学科中占有重要地位，全等三角形是整个初中阶段“图形与几何”的重点。笔者以人教版与北师版初中数学教材中的“全等三角形”为例，对两版教材全等三角形及相关知识点的编排顺序、知识点差异等方面进行比较研究，旨在探索两版教材的相似之处与不同点，并基于此对教师“全等三角形”教学及利用教材教学提供建议。

关键词：人教版;北师版;全等三角形;比较研究

一、 前言

教材是教学与学习中最核心也是最基本的资料，是教育工作者及研究者智慧的结晶。它具备一个完整的知识体系，且在教学资料上具有很强的权威性。《义务教育数学课程标准（2011）》初中学段划分为四大领域：“数与代数”“图形与几何”“统计与概率”与“综合与实践”。其中“图形与几何”中的“三角形”系列知识占了14条，是这一板块中最多的。由此可见，“三角形”在初中学段的地位很高，其重要性不言而喻。同时，“三角形”中的“全等三角形”是学生首次接触几何逻辑证明的内容，是几何证明的敲门砖，也是之后学习四边形、圆以及空间几何证明的基本工具。两版教材是如何编排“全等三角形”相关知识，有关的证明以何种逻辑顺序、结构体现，教师应如何依据教材合理安排这一部分知识点的讲解顺序等问题都值得研究。

二、 两版相关知识点编排比较

三、 两版教材编排意图分析

（一）人教版

人教版讲解全等三角形相关知识前，在前章即第十一章已阐述了三角形按边的相等关系分类、高线、中线与角平分线、三角形的内角和外角。课本习题中涉及少量的证明题，主要以解答题、计算角的度数为主。第十二章名称为“全等三角形”，表明人教版将全等三角形不仅作为某一节的内容呈现。首先，第一节以仅占一页三分之二的版面对全等形下了定义，顺理成章引出全等三角形的相关概念和性质。第二节则讲解三角形全等的判定，以第一节全等三角形的性质为引入，结合画图，探究判定两个三角形全等的条件，按照出现的顺序分别为SSS、SAS、ASA、AAS及HL，这一节的习题均与利用全等三角形的判定证明有关。第三节标题为“角的平分线的性质”，通过作图与思考得出角平分线性质的猜想，并利用全等三角形证明这一几何命题及相关命题，这一节的习题主要是围绕角平分线与全等三角形的证明题展开。第十三章轴对称的第一节涉及线段的垂直平分线的性质，并利用判定两个三角形全等的方法证明该性质。一个图形的对称轴与线段的垂直平分线有密切的关系，人教版将垂直平分线归入轴对称内容的一部分非常合理，并根据前章学习过的全等三角形对垂直平分线的性质加以证明，很好地让学生将旧知与新知联系起来。第三节是利用轴对称的知识研究等腰三角形的性质，用判定三角形全等的方法证明了等腰三角形等边对等角、三线合一、等角对等边的性质。

整体看下来，人教版将与三角形有关的内容全部放在了八年级上册，并且将与三角形证明有关的角平分线、垂直平分线与等腰三角形融入不同章节。

（二）北师版

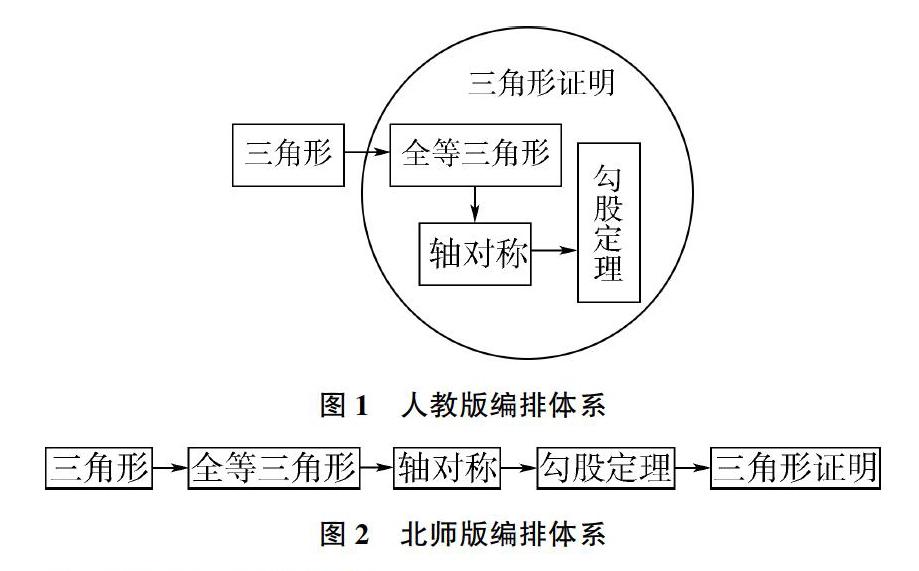
北师版不同于人教版，并未将三角形相关内容放在同一册书，而是分布在三册书中。其中，七年级下册第四章第一节和人教第十一章非常相似，讲解了三角形基本知识和分类、中线与高线。不同的是，其并没有讲解角平分线，三角形的内角和外角也没有涉及。在第二节专门讲解图形的全等，并引出全等三角形的概念，这部分内容人教版也放在一整节内容进行讲解。第三节是探索三角形全等的条件，直接通过画全等三角形引入，根据作图与讨论分别得出SSS、ASA、AAS及SAS判定两个三角形全等的条件，并没涉及HL，将其放在了八年级下册三角形的证明中。值得一提的是，北师大在本章的第四节和第五节专门进行了尺规作三角形和利用三角形全等测距离讲解，有一定的特色。在人教版在第十一章三角形讲解完后，直接进行全等三角形的讲解，并在第三节专门提到角平分线。北师版则是通过七下第五章轴对称衔接第四章三角形，在第二节探索轴对称的性质中第一次为垂直平分线进行铺垫，并在第三节着重讲解等腰三角形三线合一，对垂直平分线下定义及角平分线的性质。至此，并没有涉及有关三角形的证明，而是在八年级下册第一章进行讲解。与之前所学的相关概念隔了整整两个学期。同时，在八年级上册进行了勾股定理和三角形内角和定理的讲解，这与人教版也有很大的不同。人教版直接在第十一章就已经讲解了三角形内角和定理，而北师版将这一定理归在了平行线相关知识下。且人教版在三角形、全等三角形、轴对称、三角形相关证明后，在八年级下册进行勾股定理讲解。北师版则将勾股定理放在了三角形、全等三角形、轴对称和三角形证明的中间部分，图1和图2可以直观体现。

整体看下来，北师版不像人教版将三角形相关内容放在同一册书，而是分布在三册书中。而且其编排顺序和人教版有明显差异，相同知识点的呈现方式、重复率也不同。

图1人教版编排体系

图2北师版编排体系

四、 对教师教学建议

上述对人教版和北师大版关于“全等三角形”相关知识点的编排、内容分布等进行了比较。对比发现，两版教材有相似之处，但也存在非常明显的差异。如：人教版将与全等三角形相关的大部分内容放在一学期进行讲解，北师版则是分散在三个学期进行;两版教材判定三角形全等的条件出现顺序不同;人教版将三角形证明融入三部分内容，而北师版将其系统的放在了一章。

将知识点分布在三个学期或是两个学期并不值得深究。因為，数学学科最大的特点就是不靠生硬的熟记概念和定理，且其难度是螺旋上升。故学生并不会因时隔一学年就忘记之前学过的简单知识点。然而，判定全等三角形的条件共有五个，最特别的是HL。人教版将五个条件放在同一节，北师版将HL放在八年级下册，与其他四个判定全等的条件相差了两个学期。这一安排是否合理，作为教师并不能轻易下结论。北师版HL定理的得出借助了勾股定理，因此勾股定理必然需要在其之前讲解，有了勾股定理的插入，知识点的编排顺序就需要重新考虑。人教版HL定理的得出并未借助证明，而是直接由探究活动得出。因此，人教版便将勾股定理单独放在八下讲解。知识点环环相扣，呈现方式教材也有差异，教师在备课时不仅应考虑某一学期、某一章节的内容，更应放眼整个大的知识体系。从宏观和微观两个角度出发，合理安排知识点呈现顺序，并且及时总结归纳以更好让学生将新知旧知联系起来。

若教师使用的教材是人教版，那么教师可以在十三章轴对称讲解完垂直平分线性质和等腰三角形相关证明后，对上一章涉及的角平分线性质及直角三角形的证明再次提出，将这四个证明归属于三角形的证明中。这样便与北师版八下第一章不谋而合，且学生对三角形的证明更加深刻系统。同时，在八下勾股定理讲解完后，教师可以和学生共同思考是否可以借助勾股定理得到HL判定全等的定理，因为之前定理的得出仅是通过探究，没有经历严格的证明。

若教师使用的教材是北师版，那么教师可在全等三角形条件中先向学生讲解HL判定定理，这样便可完整的让学生掌握所有的判定定理。同时利用判定全等三角形的条件，适当讲解有关等腰三角形、垂直平分线与角平分线的性质证明。总之，全等三角形是学生初次规范接触严密的推理证明，教师应给予学生尽可能多的探索，注重培养“四基”与“四能”，绝不可照搬教材的讲解模式。

五、 总结

教师教学，教材当然是第一重要的。然而，教材是固定的，教师却是灵活的，学生是活泼的，课堂是生动的。新时代的教师不只是教书者，更是教育教学的研究者。教师的教学内容不应一味跟着教材走，应该结合课程标准、学校教研活动、学生学情等多方面综合考虑，制定一套合理动态的教学内容，并在实施过程中不断改进。

教师是教学的灵魂，教师应从“教教材”上升为“用教材教”的境界，活用教材。教师教什么，教材中已经有所体现，但如何教却不能由教学知识规定。“活教”的教师更能教出“活学”的学生。

参考文献：

[1]中华人民共和国教育部.义务教育数学课程标准（2011年版）[M].北京：北京师范大学出版社，2012.

[2]李胜兰.初中“全等三角形”内容设置变迁之研究（1951～2013年）[D].内蒙古师范大学，2019.

作者简介：

吴限，刘素红，陕西省宝鸡市，宝鸡文理学院。