自适应触发下一类神经网络的安全同步控制

刘 延，刘清怡

（南京财经大学应用数学学院，江苏南京210023）

神经网络是一种非线性动态系统，在参数选取得当的情况下，可以表现出很大的复杂动态特性.由于近年来成功地应用在信号处理、模式识别、全局优化等[1]领域，神经网络的研究受到了广泛的关注.同时，由于同步控制的潜在应用，如信息处理、机器人阵列、安全通信等，同步控制[2-4]研究引起了更多学者们的注意. 在这些同步问题中，驱动-响应同步是一个流行的话题. 驱动响应同步的基本原理是，驱动系统向响应系统发送信号，然后响应系统通过使用该信号来使自身与驱动系统达到同步. 换句话说，响应系统受驱动系统行为的影响，但驱动系统与响应系统无关. 然而，对于具有时变时滞的非线性神经网络系统的驱动响应同步控制还没有得到充分的研究，这是本文的第一个动机.

值得注意的是，由于网络带宽的限制，网络控制系统和现代通信技术的发展常常带来一些挑战. 由于任何通信网络单位时间内只能携带有限的数据，因此，如何减轻网络的负担，提高网络传输的效率，已经成为人们研究的热点[5-7]. 作为传统周期控制模式的一种替代方案，事件触发方案在网络化控制系统中得到了广泛的关注. 差异在于事件触发方案设置一个触发条件来确定是否应该发送采样数据，这样可以减少网络带宽的负担和功耗. 但是，传统的事件触发所设置的触发阈值几乎都是常数，节约的资源有限. 因此，具有动态阈值的自适应触发机制[8-10]被设计出来并得到广泛运用.

众所周知，在某些实际系统中可以发现非线性. 由于物理上的限制、技术上的限制或其他内部因素的影响，作为一种缺少测量的现象，饱和非线性经常存在于许多网络控制系统中. 近年来，输入饱和的研究成为热点，网络系统中的一些研究成果[11-13]也层出不穷.但是，对于具有控制输入饱和的神经网络系统，在开放式文献中几乎没有基于驱动响应同步的控制结果. 在理论和实践中，这个问题都是很重要和具有挑战性的. 在此基础上，本文研究了具有输入饱和的神经网络驱动响应同步控制问题，这是本文的第二个动机.

在实际工程应用中，由于控制元件（如传感器、控制器、执行器等）都是通过共享通信网络连接，来实现有效的远程控制，故容易受到恶意攻击（包括DoS 攻击、欺骗攻击、隐身攻击等[14-17]），因此安全问题是研究与发展的一个重要课题. 值得指出的是，关于神经网络的驱动响应同步问题，开放文献中对于网络安全方面的研究较少，基于此，在驱动响应同步基础上，提出网络攻击环境下一种基于自适应触发的具有输入饱和的输出反馈控制方法，这是本文的第三个动机.

基于上述观点，本文对网络攻击和输入饱和环境下时滞神经网络的自适应同步控制问题进行了研究. 利用李雅普诺夫稳定性理论与线性矩阵不等式提出了一套新的时滞相关稳定性准则，通过自适应事件触发采样来实现神经网络驱动响应系统的同步. 基于这种稳定条件，提出一种神经网络自适应事件触发输出反馈同步控制器的设计方法，并给出数值算例，以说明该方法的有效性.

1 问题陈述与建模

考虑如下时滞神经网络作为驱动系统：

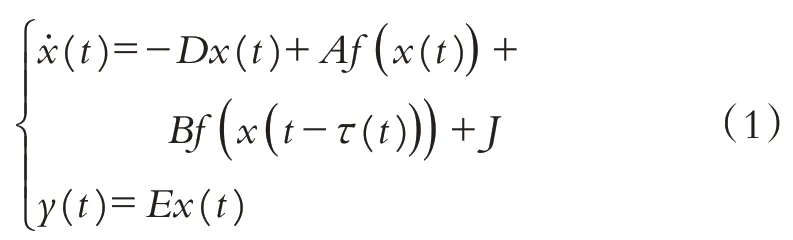
其中x(t)=(x1(t),x2(t),…,xn(t))T∈ℝn是表示n个神经元的状态向量，D、A、B和E是已知的系数矩阵，τ(t)∈[0,τ]是时变的有界时滞，J表示输入偏差.f(x(t)) 表示神经元激活函数且满足f(0)=0.

根据驱动系统，给出相应的响应系统模型：

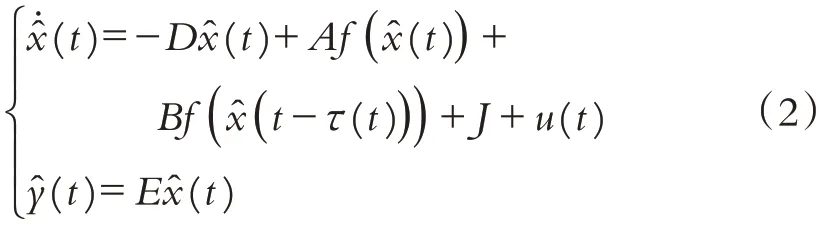
其中^(t)表示响应系统的状态，u(t)是控制输入.

定义e(t)=(t)-x(t)作为同步误差的状态，则误差系统模型如下：

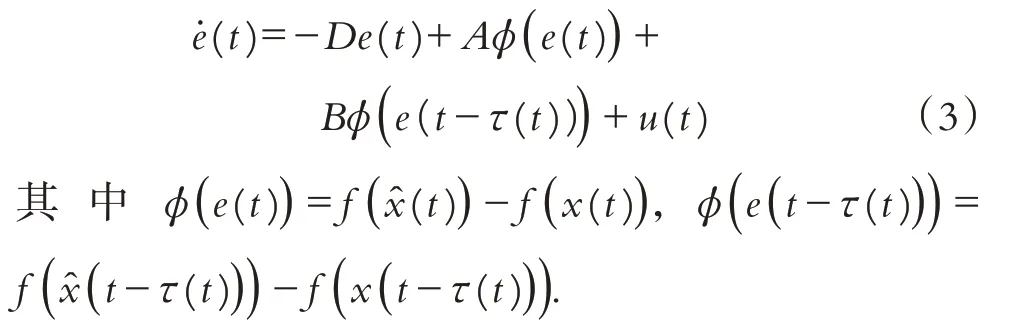
实际操作中，周期性采样方法会降低数据传输效率，浪费网络带宽. 为了节省网络资源，在传感器和控制器之间引入了一种自适应事件触发方案，用于确定是否应将输出误差发送给控制器. 定义作为将传输给响应系统控制器的采样测量误差.

假定网络通信中的时变延迟为dk∈[0,d](k=1,2,…,∞)且采样周期为h. 考虑到时延的影响，采样测 量将分别在t1h+d1,t2h+d2,t3h+d3,…时刻到达控制器，则自适应触发规则为：

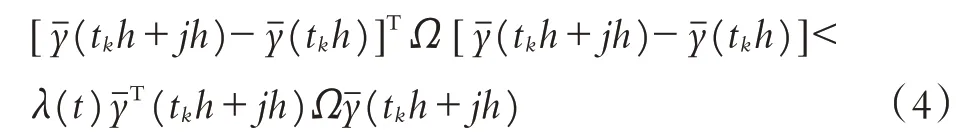
其中Ω是一个正定矩阵，且λ(t)满足如下条件：

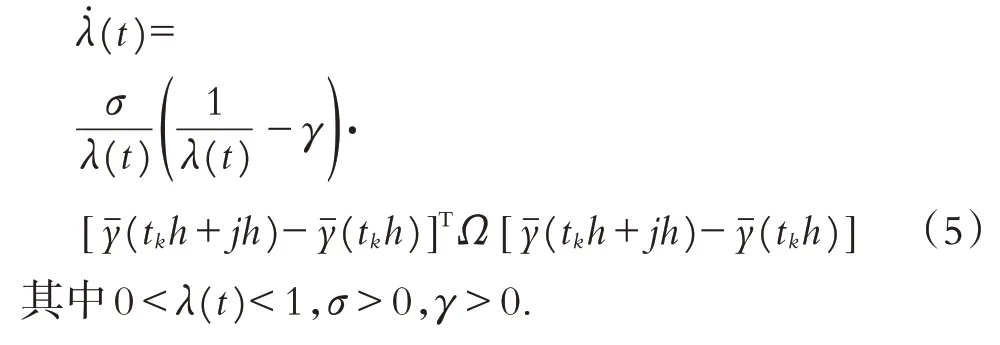
当前采样数据yˉ(tkh+jh)能被传输当且仅当当前采样数据yˉ(tkh+jh)与上一传输数据yˉ(tkh)违反不等式（4）.

为了技术方便，类似于文献[12]，定义d(t)和ek(t)如下：

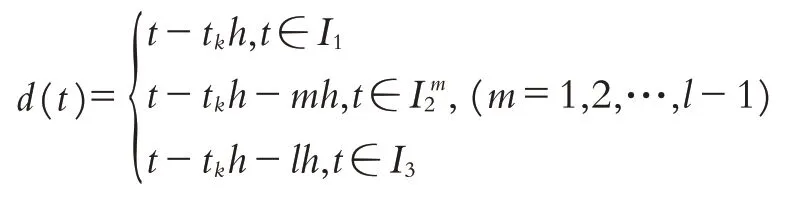
并且0≤d(t)＜dM，其中dM=h+d是d(t)的上界.

根据上面d(t)和ek(t)的定义，式（4）和式（5）可以重新写为

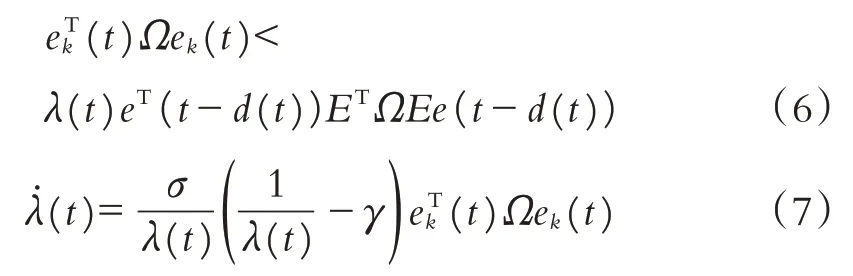
因此，基于事件触发机制与网络延迟效应，控制器的实际输入如下：

其中k是相应的控制器增益矩阵.

在此，引入饱和函数的定义如下：

其中

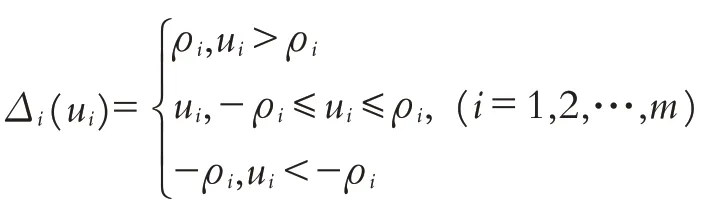
基于文献[18]的结果，饱和后的实际输入以下列形式表示：

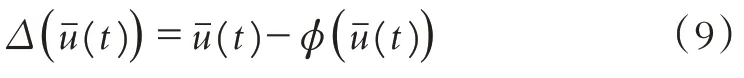
其中φ(u^(t))是一个非线性函数，且满足如下不等式

其中0＜ε＜1.

在网络系统的实际应用中，恶意网络攻击或干扰可能经常发生. 本文假设攻击信号是一种随机干扰，可以用一个与网络节点动态行为有关的非线性函数h(·)来描述.则网络攻击环境下，实际输入为：

其中α(t)表示满足伯努利分布的网络攻击概率，取值介于0 和1 之间，并假设P{α(t)=1}=α，P{α(t)=0}=1-α，则攻击概率的期望为E{α(t)}=α，方差为ρ2=α(1-α).

结合（6）-（11）式，最终误差系统模型如下：

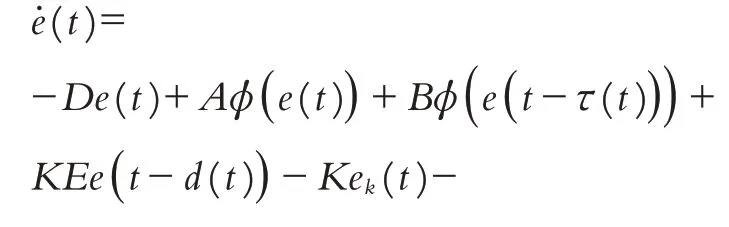
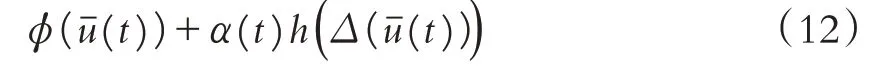
为证明主要结果之前，引入下面的假设和引理.

假设1神经元激活函数f(·)和网络攻击信号函数h(·)为连续非线性函数，且满足如下Lipschitz条件：

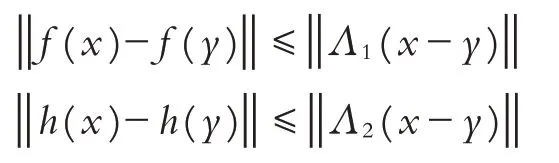
其中Λ1和Λ2是常数矩阵，且分别表示f(·)和h(·)的上界.

引理1[19]给定常数m，若函数d(t) 满足d(t)∈(0,m]，则对于存在矩阵R＞0，使得如下矩阵不等式成立：

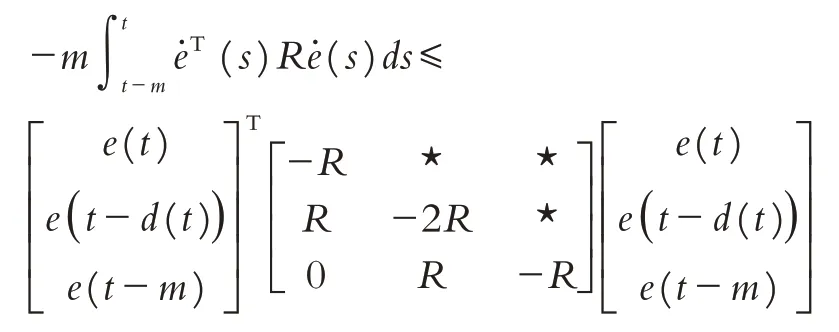
引理2[20]（Schur 补引理） 对于给定矩阵S=其中如下条件是等价的：

2 主要结果

这个部分给出相应定理来分析闭环误差系统（12）.利用李雅普诺夫泛函方法，首先给出了渐近稳定的充分条件. 然后，应用线性矩阵不等式方法，求解非线性项并给出响应系统（2）的输出反馈控制器设计.

2.1 稳定性分析

定理1对于一些给定的正标量参数τ,dM,σ,γ,α,ε,ε1和ε2，系统（12）在输出反馈控制器K下是渐进稳定的，如果存在合适维度的矩阵P＞0,Qi＞0,Ri＞0,(i=1,2),Λs(s=1,2,3),Ω＞0，使得如下不等式成立：

其中

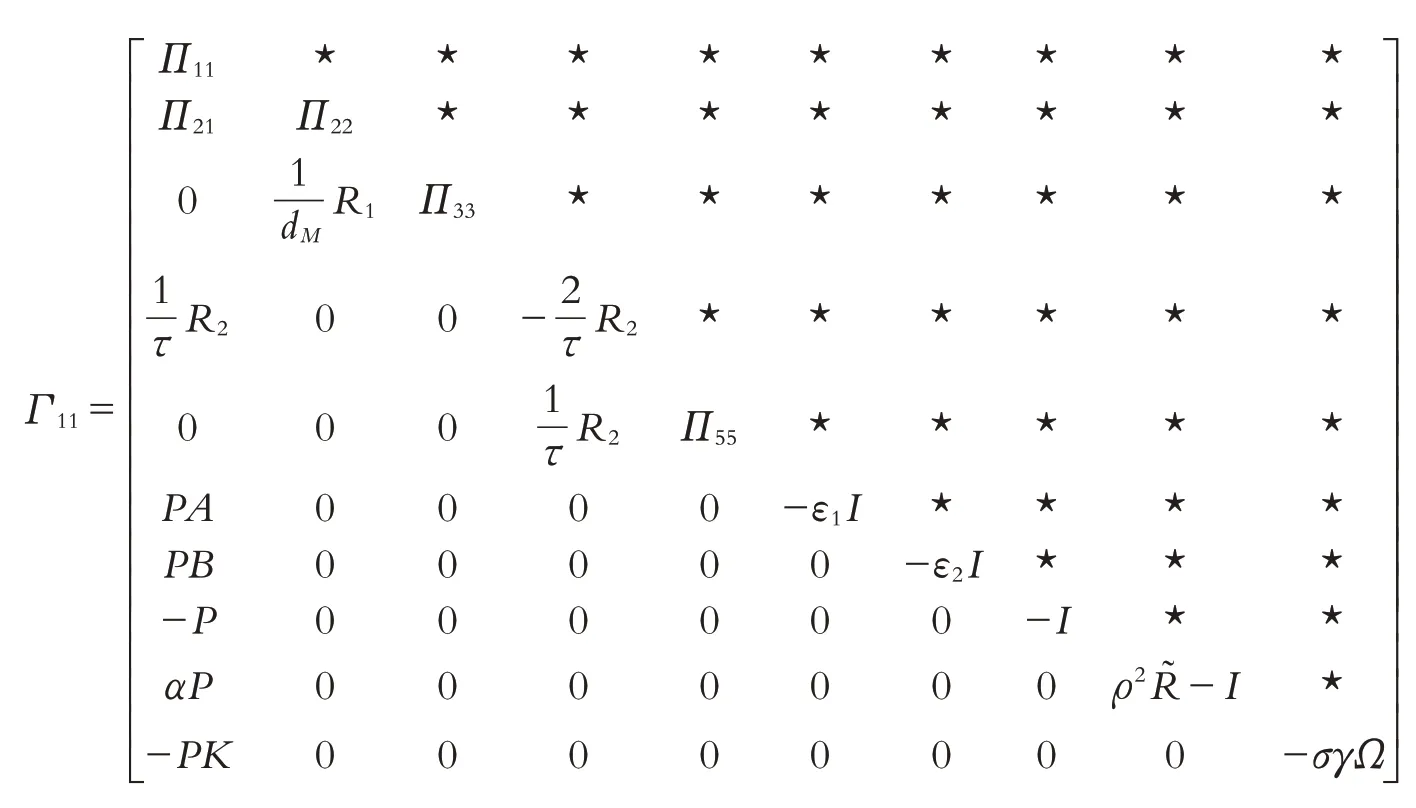
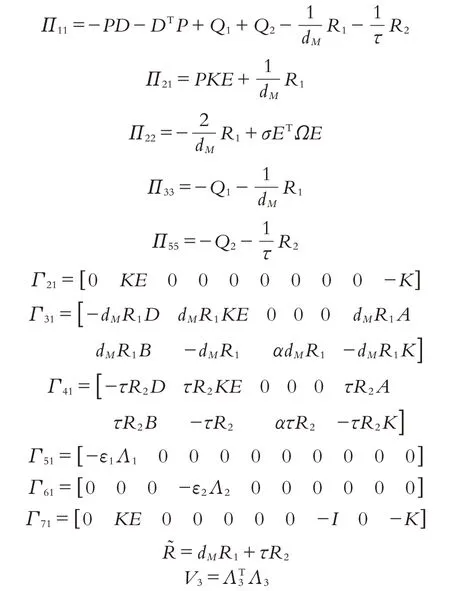
证明：建立如下形式的李雅普诺夫泛函

其中

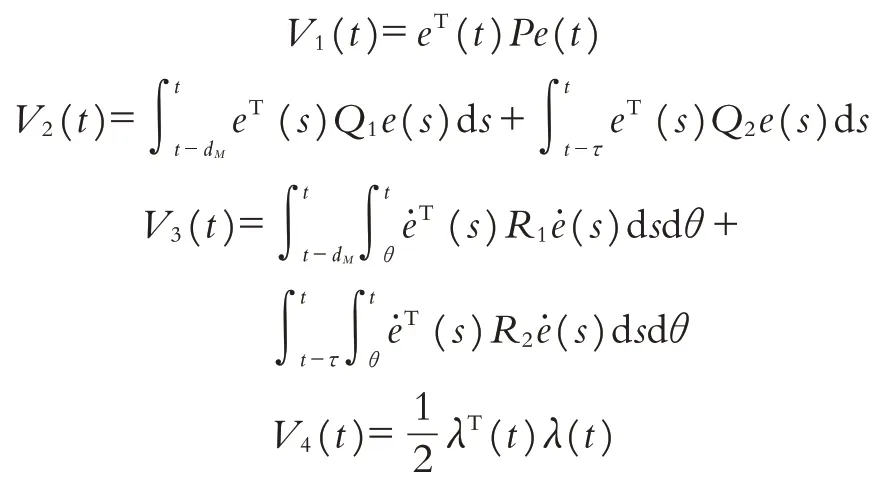
其中P＞0,Qi＞0,Ri＞0,(i=1,2)是待定的对称矩阵.

对V(t)关于t求导求期望可得：

结合（6）式与（17）式，可以推出

E{V˙4(t)}≤

因此，可以推得

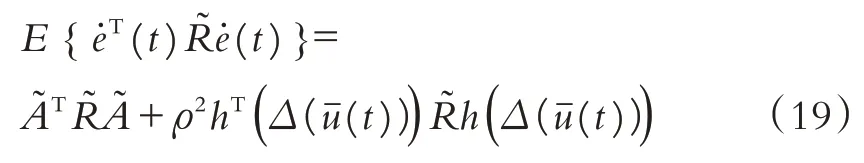
根据假设1，可以得到如下不等式：

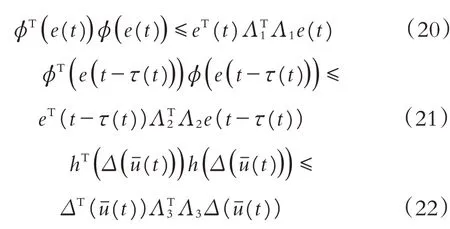
结合（14）-（22）及引理1，可以得到不等式：

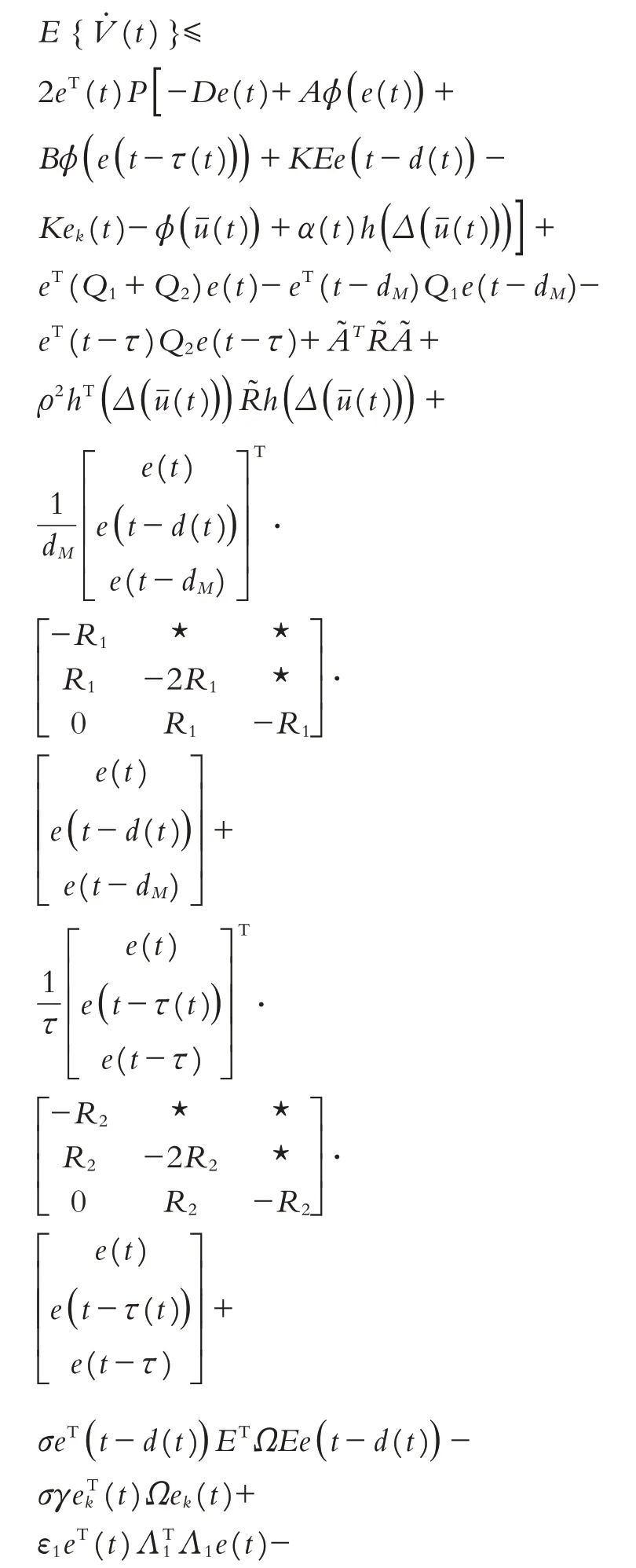
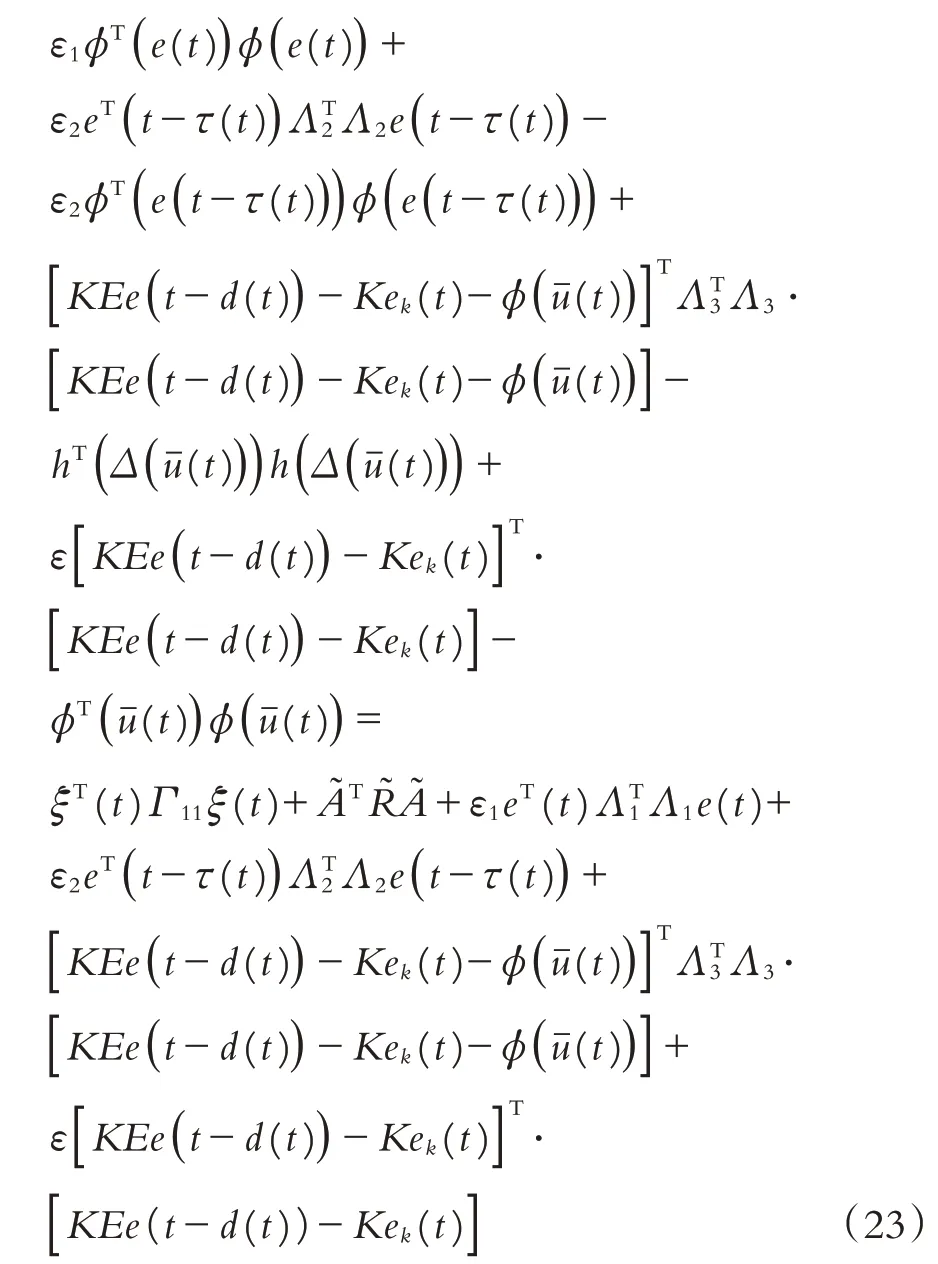
其中

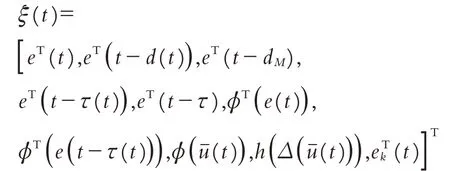
运用引理2，即可推得式（23）等价于ξT(t)Γξ(t)，由Γ＜0 可知E{V˙(t)}＜0，因此得证系统（12）是渐进稳定的.

由于定理1 中矩阵不等式中非线性项的存在，不等式（13）不能直接用MATLAB 的LMI 工具箱求解.可在下面的定理2中解决此问题并设计控制器.

2.2 控制器设计

定理2对于一些给定的正标量参数τ,dM,σ,γ,α,ε,ε1,ε2，系统（12）在输出反馈控制器K=P-1V下是渐进稳定的，如果存在合适维度的矩阵P＞0,Qi＞0,Ri＞0,(i=1,2),Λs(s=1,2,3),Ω＞0 和V，使得不等式（24）成立：

其中

其他参数在定理1中已定义.

证明：令K=P-1V. 对（13）式先左乘右乘矩阵再左乘右乘矩阵diag{I,P,P,I,I,I,P}，则可以得到：

再考虑如下不等式

由此，可以从（25）式推导出（24）式，完成证明.

3 数值仿真

参考文献[21]，考虑神经网络的系统参数如下：

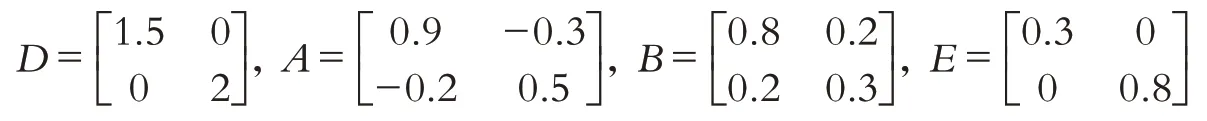
参考文献[22]，假设神经元激活函数f(x)和网络攻击函数h(x)分别为：

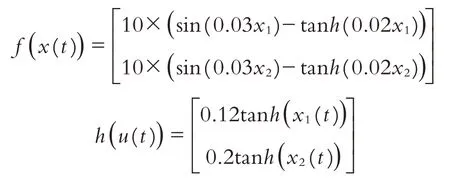
且输入偏差J=0.

基于假设1，经过简单的计算，可得：

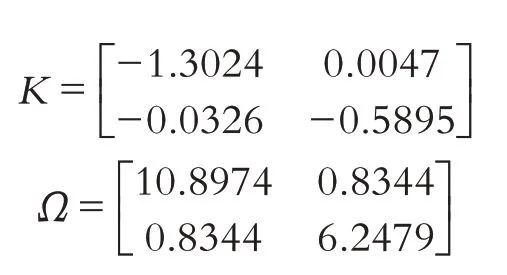
然后，令参数τ=0.1,dM=0.1,α=0.5,ε=0.4,ε1=2,ε2=3,γ=15，事件触发参数σ=0.2. 根据定理2 运用线性矩阵不等式方法求得下列可行解：

控制器增益矩阵和事件触发矩阵如下：

基于上述结果，设定采样周期h=0.1 并选取初始值x(0)=[-0.3 0.3]T，x^(0)=[0 0]T，自适应初始触发值λ(0)=0.3. 可以得到仿真结果如图1-4 所示（注：每个图的横坐标表示时刻，单位为秒. 图1、3、4的纵坐标表示相应的状态. 图2 的纵坐标表示触发间隔，单位为秒）. 图1 显示了在控制器下，同步误差快速趋于0，这表明最终系统是同步且稳定的. 图2显示了自适应事件触发的触发时刻与间隔，很明显看到其有效节约了网络资源，避免不必要的信号传输. 图3 显示了触发阈值随时间在发生变化. 图4 展示了网络攻击的变化情况. 综合上述仿真结果可见，本文的方法是可行且有效的.

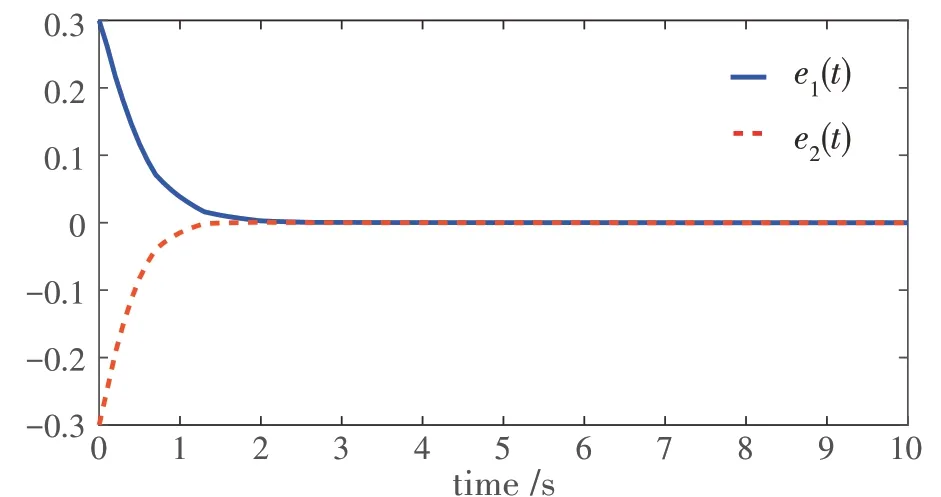
图1 同步误差e(t)的值与时间t的关系

图2 自适应事件触发的触发时刻与间隔

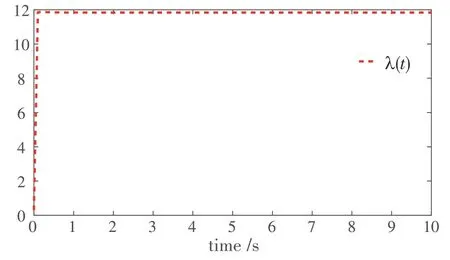
图3 自适应触发阈值λ(t)与时间t的关系

图4 网络攻击信号h( Δ( (t)) )与时间t之间的关系

4 总结

本文研究了网络攻击和输入饱和环境下，时滞神经网络的自适应事件触发驱动-响应同步控制问题. 采用基于输出误差反馈的自适应事件触发机制，减少控制器更新次数，避免不必要的网络资源浪费，并充分考虑网络攻击和输入饱和的影响，通过李雅普诺夫泛函得到了使同步误差系统渐近稳定的充分条件，然后利用线性矩阵不等式技术同时得到控制器的增益矩阵和事件触发参数矩阵. 最后，给出了一个仿真例子来说明最终结果的有效性.