时空联合的鼠兔视频序列图像分割
胡士亚,陈海燕,葛 浩
(1.滁州学院机械与电气工程学院,安徽滁州239000,2.兰州理工大学计算机与通信学院,甘肃兰州730050)
高原鼠兔(Ochotona curzoniae)是主要活动于我国海拔3 000 m ~5 100 m 的高寒草原地区优势种鼠害之一,甘南藏族自治州高原鼠兔的危害尤为严重,因此,监测鼠兔活动对指导高原草地的生态保护工作、积极响应国家生态文明建设具有十分重要的意义. 随着视频监控、图像处理、机器视觉等技术的快速发展,获取高原鼠兔的研究数据变得更加便捷,而在自然生态环境下对高原鼠兔进行智能监测,视频序列图像分割是系统中关键技术之一[1].
高原鼠兔生活的草原环境异常复杂,鼠兔毛色与枯萎的草地颜色十分相似,尤其秋冬季节表现更为明显,因此鼠兔视频序列图像突出的特点就是对比度较低. 除此之外,由于高原鼠兔运动的突变性,导致鼠兔视频序列中一部分帧的运动目标处于快速运动状态,另一部分帧的运动目标处于静止观察状态,因而鼠兔视频序列图像的分割尤为困难.
分割视频序列中的运动目标大都采用基于活动轮廓模型的方法[2],其主要思想可分为两个阶段,第一阶段:空间域上,先对视频序列图像进行粗分割,主要采用常规运动目标检测方法,为活动轮廓模型获取初始轮廓曲线. Stauffer 等人[3]提出了鲁棒性较高的混合高斯背景建模法,但算法复杂度较高,无法实时处理鼠兔视频序列. 肖军等[4]提出的光流法计算较为复杂,且抗干扰较弱,因此不适用复杂背景下的小目标检测. 第二阶段:主要采用活动轮廓模型实现视频序列的精确分割. 赵骥等人[5]提出一种改进的测地活动轮廓模型,先用帧间差分法检测运动目标的轮廓边界,再用改进测地活动轮廓模型进行迭代演化,但对于边缘较弱的鼠兔图像效果不佳.胡祝华等人[6]提出一种改进的距离规则水平集演化方法,在帧差法基础上,对运动目标进行分割. 徐杨等人[7]提出一种背景差分方法与改进的活动轮廓模型相结合的分割算法,让曲线演化且收敛于真实目标边界. Kompatsiaris 等[8]提出对运动目标用K 均值聚类算法进行粗分割,再利用基于贝叶斯的时域跟踪模型进行精分割. 由于光流法计算复杂、背景减除法背景获取困难及传统活动轮廓模型分割精度问题[9],传统的时空联合分割方法无法有效处理鼠兔视频中的运动目标. 因此,本文根据高原鼠兔运动的突变性和鼠兔图像对比度低的特点,提出一种适合鼠兔视频序列图像自身特点的高效分割方法. 在时间域上,采用本文提出的一种基于帧间差分法的快速目标检测算法,在空间域上,采用张爱华等人[10]提出的改进LBF 模型,可精确分割出鼠兔视频序列图像中的运动目标.
1 时空联合分割
1.1 时域的目标分割
鼠兔视频序列图像的初始轮廓曲线精确获取是后期精确分割的关键,因此首先对鼠兔视频序列图像采取两帧帧间差分法进行处理:
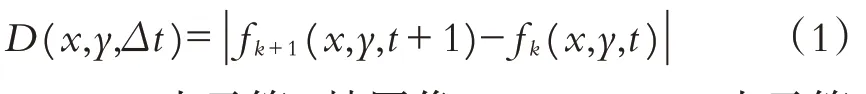
其中:fk(x,y,t)表示第k帧图像,fk+1(x,y,t+1)表示第k+1 帧图像,D(x,y,Δt)为第k帧与第k+1 帧之间的差分图像,x和y是像素坐标,t表示视频序列中的某一时刻.
再经过二值化处理得到二值化后的差分图像B(x,y,Δt):
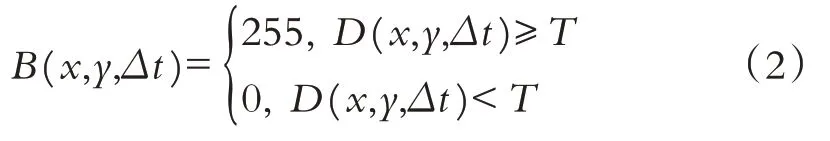
其中:T是二值化处理时选用的阈值,它与两帧帧间差分后图像的像素的平均值和标准差δ有密切联系,可通过、δ这两个参数来设定,计算如下:
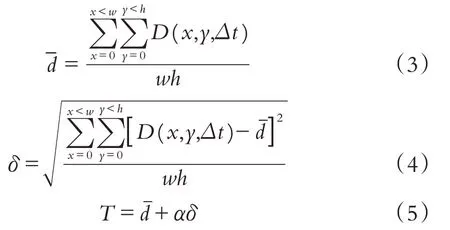
其中:α为阈值微调系数,可根据需要调节;w为图像宽度;h为图像高度.
由于鼠兔视频序列图像对比度较低,差分图像经过二值化处理后存在“空洞”现象,故先引入形态学开闭重构运算,最大化地连接二值图像的“空洞”区域,再通过遍历整个二值图像,找出每一幅二值图像中面积最大的二值区域,根据下式
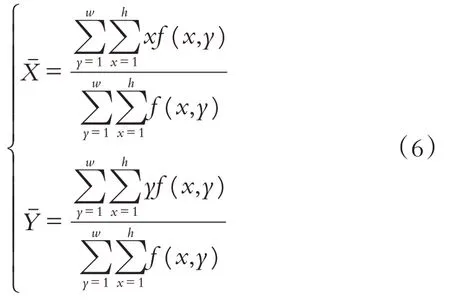
计算得到最大的二值区域的质心. 通过多次观察实验发现,可根据质心坐标设置大小为60 pixel × 40 pixel的红色外接矩形框.
图1给出了第k+1帧鼠兔获取初始位置的简易流程图. 由于高原鼠兔运动的突变性,视频序列图像中目标的状态主要可分为两种:静止观察和快速运动. 鼠兔运动的突变性给数据采集带来极大困难,通常都是先选择静止观察状态的鼠兔目标来拍摄,因此,采集的大部分鼠兔视频前面数帧中的运动目标都处于静止观察状态,相邻帧之间几乎没有像素变化,无法直接采用两帧帧间差分法获取第1 帧图像的初始位置. 故而先对第1 帧图像采取手动分割方法来获取鼠兔目标的初始轮廓曲线,从第2 帧开始,每一帧与前一帧进行两帧帧间差分,若检测到相邻两帧图像之间像素变化(二值区域面积)小于预设阈值(本文选取25),则表示此刻的鼠兔处于静止观察状态,那么当前帧的初始轮廓曲线与上一帧的相同;如果检测到相邻两帧鼠兔图像像素变化大于等于预设阈值,则表示此刻的鼠兔处于快速运动状态,那么算法将自动重新计算差分后二值区域的质心坐标,根据质心坐标重新获得外接矩形框,即为当前帧的初始轮廓曲线.

图1 获取k + 1帧图像初始位置的简易流程图Fig.1 Flow chart of k + 1 frame image initial position is obtained
1.2 空域的目标分割
LBF 模型[11]由Li 等人提出,其能量泛函定义如下:
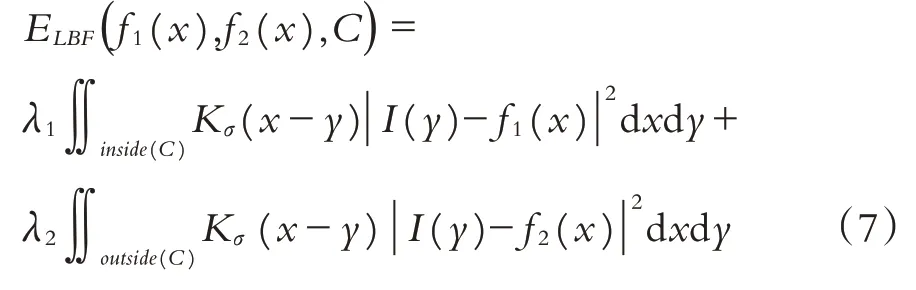
其中:λ1和λ2为正整数,通常设λ1=λ2=1;I(y)为图像;C为活动轮廓曲线;f1(x)和f2(x)分别为图像像素点x在C内部与外部的灰度拟合值,像素点x邻域内各个像素y∈o(x)可确定灰度拟合值;inside(C)和outside(C)分别表示活动轮廓曲线的内部区域与外部区域;Kσ(x-y)是高斯核函数,通常为:
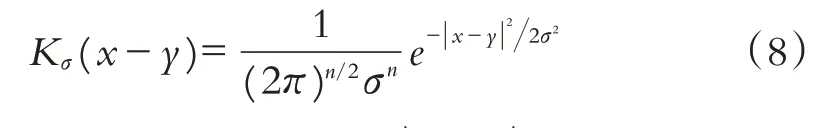
其中:σ为标准偏差,σ>0;当| |x-y增加时,Kσ(xy)减小并且逐渐趋于零.
采用梯度下降法获取偏微分方程:
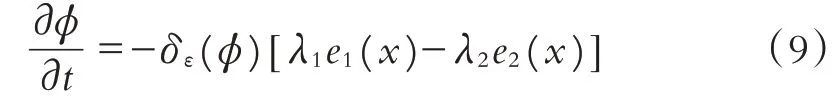
则局部拟合函数f1(x)、f2(x)以及e1(x)、e2(x)分别为:
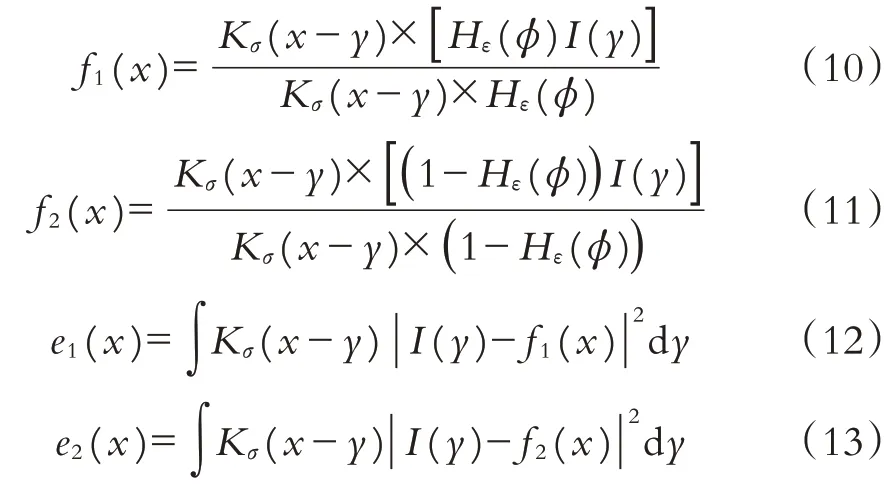
由于在水平集函数演化的过程中LBF轮廓模型极易陷入局部最小值,文献[10]提出将全局图像梯度信息引入LBF 模型中. 假设原图为g(x,y)(以下用g表示),由于圆盘形状结构元素难以促使图像特征值发生畸变,所以选择圆盘状结构元素为B(x,y)(以下用B表示),灰度图像形态学梯度定义为:
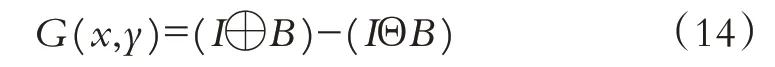
式中:⊕和Θ分别表示灰度形态学膨胀和腐蚀运算,I表示形态学开闭重构后的图像,G(x,y)表示获得的形态学梯度图像.
图像的一个重要特征是图像梯度,在水平集函数演化过程中可作为引导信息. 文献[10]借鉴Chan-Vese 模型能量函数构造思想,构建包含图像梯度信息的模型:
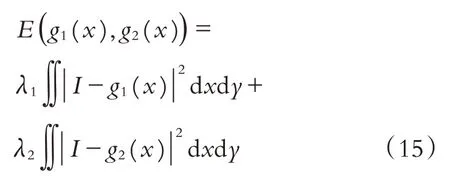
式中,全局梯度拟合函数g1(x)和g2(x)类似于Chan-Vese 模型中的封闭轮廓曲线内外的灰度平均值c1和c2.g1(x)和g1(x)分别定义如下:
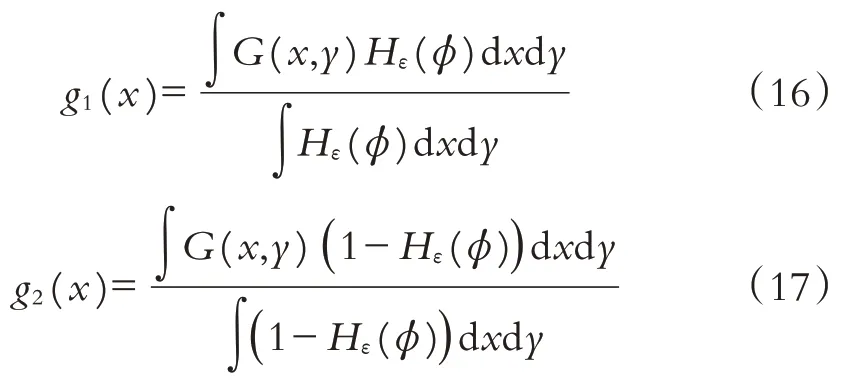
定义f1(x)和g1(x)以及f2(x)和g2(x)的线性组合为u1(x)和u2(x):
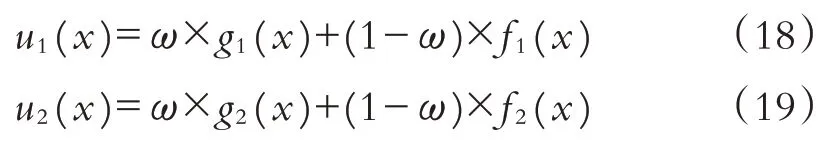
式中:ω为加权系数,0 ≤ω≤1.
则本文所提出的分割模型能量函数E(u1(x),u2(x),φ)定义为:
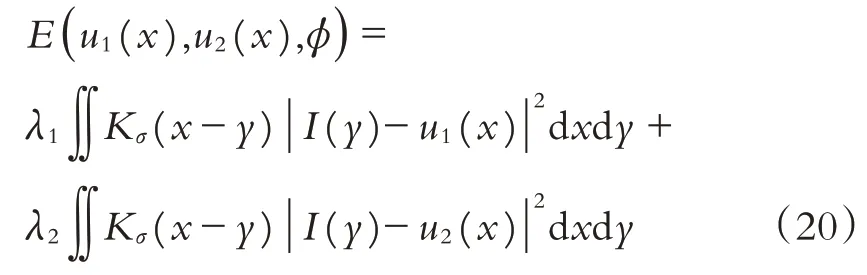
为避免水平集函数对距离函数发生偏离,且为了水平集函数迭代演化过程中不重新初始化,将距离规则项添加到能量函数中,即:
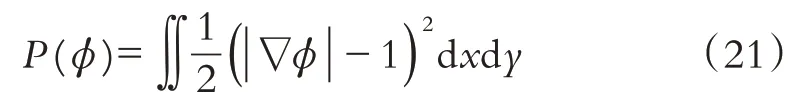
式中:∇为梯度算子;| |
·为梯度模值.
同时通过添加长度项规范轮廓曲线的演化来规范水平集活动轮廓曲线,长度项为:
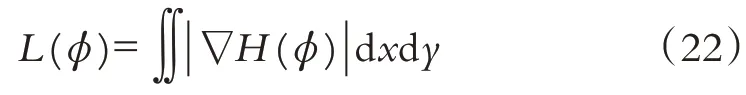
最后采用梯度下降流法,求出水平集演化方程:

式中:∇2为拉普拉斯算子;div(·)为散度算子;μ为长度项权重因子;ν为面积项权重因子;h1(x)和h2(x)分别为:
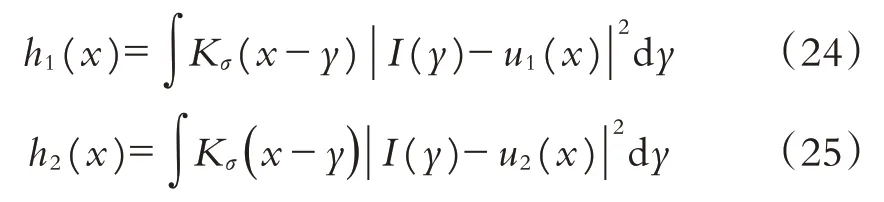
2 算法的实现
图2 为本文提出的视频序列图像分割流程图,主要分为两个步骤:第一步利用时域信息获取当前帧图像的初始轮廓曲线,采用本文提出的一种基于帧间差分法的快速目标检测算法,对k帧和k+1 帧鼠兔视频序列图像进行两帧帧间差分,再判断当前帧鼠兔目标的运动状态,最后确定当前帧的初始轮廓曲线;第二步利用空域信息获取运动目标轮廓,为了增强图像中背景与目标的对比度,先对其做形态学开闭重建运算,再采用改进LBF 模型对重建后鼠兔图像进行迭代演化.
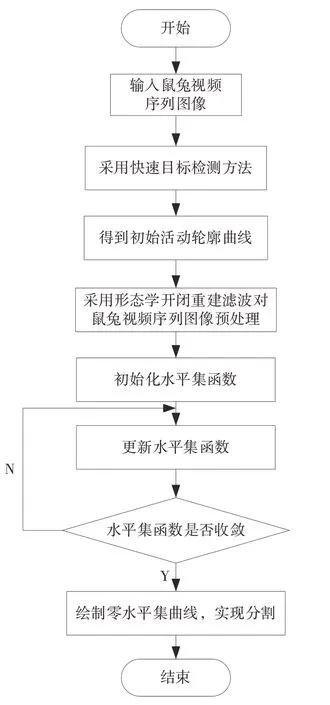
图2 本文方法分割流程图Fig.2 Segmentation flow chart of proposal method
3 实验与结果分析
算法实验采用MATLAB R2013a,在戴尔PC(Intel Core™i5 CPU @2.5 GHz)64 位操作系统上进行算法的仿真. 选取课题组秋冬季节在甘南藏族自治州下辖的碌曲县草原拍摄的高原鼠兔视频作为实验数据. 选用一段共80 帧的鼠兔视频,视频中的第1 帧至第25 帧和第53 帧至第80 帧的鼠兔目标处于静止观察状态,第26帧至第52帧的鼠兔目标处于快速运动状态.
实验中,三种分割方法均先采用快速目标检测方法确定当前帧鼠兔图像的初始轮廓曲线,且参数设置相同. 涉及的参数设定如下:时间步长τ=0.1,计算Dirac规则化函数δε(φ)和Heaviside规则化函数Hε(φ)时所用的空间步长h=1,规则化参数ε=1,选取参数λ1=λ2=1,σ=3,ν=0,μ=0.01×255×255.
为了验证算法的有效性,随机从80 帧的鼠兔视频中选取四帧(第27、37、47、57 帧)进行对比分析,如图3 中的(a)-(d)所示,其中处于运动状态的鼠兔目标有第27、37、47 帧,处于静止状态的鼠兔目标只有第57帧.图3中的(e)、(f)、(h)分别为对其采用本文提出的快速目标检测方法得到的初始轮廓曲线.由于图3 中的(e)、(f)、(g)检测目标处于运动状态,利用快速目标检测方法可快速得到鼠兔目标的初始位置. 图3 中的(h)鼠兔目标处于静止状态,未检测到相邻两帧有一定的像素变化,所以此时当前帧(第57帧)初始轮廓曲线沿用第56帧的轮廓曲线.

图3 快速目标检测方法Fig.3 The method of fast target detection
第27、37、47、57 帧鼠兔运动目标的初始轮廓曲线如图4(a)-(d)中的红色矩形框,图4中的(e)-(h)分别为LBF模型分割结果.实验中,LBF模型的迭代次数设置为50次.
实验结果表明,由于鼠兔视频拍摄于复杂的自然生境环境,背景较为复杂,且含有大量的噪声干扰,使得分割结果中存在大量的假轮廓.

图4 快速目标检测与LBF模型相结合方法Fig.4 The method of combining fast target detection with LBF model
第27、37、47、57 帧鼠兔运动目标的初始轮廓曲线如图5(a)-(d)中的红色矩形框,图5中的(e)-(h)分别为RSF 模型的分割结果. 实验中,RSF 模型的迭代次数设置为10次.
实验结果表明,RSF 模型分割结果与LBF 模型分割结果存在同样的问题,由于种种客观因素的影响,使得分割结果中存在大量的假轮廓,目标边界分割不精确.
最后采用本文提出的快速目标检测与改进LBF模型相结合的分割方法,分割开闭重建滤波后鼠兔视频序列图像. 实验中,改进LBF 模型的迭代次数设置为40 次. 第27、37、47、57 帧鼠兔运动目标的初始轮廓曲线如图6(a)-(d)中的红色矩形框,而图6中(e)-(h)分别为改进LBF模型的实验分割结果.
实验结果表明,虽然经过曲线的迭代演化,基本上都能定位到鼠兔目标的轮廓,但由于图像自身存在的分割问题点,鼠兔快速运动致使图像中的目标局部边缘模糊,另外改进LBF 模型依然对初始轮廓曲线位置较敏感,从而使得分割不够彻底、轮廓定位不够精确.

图5 快速目标检测与RSF模型相结合方法Fig.5 The method of combining fast target detection with RSF model

图6 本文方法Fig.6 Proposal method
为了验证本文算法的性能,需要定量分析算法的分割精度和算法复杂度. 对于分割精度,根据文献[13]中提出的用于静态图像的评判指标相似度指数S,提出了用于鼠兔视频序列图像的评判指标平均相似度Savg;在算法复杂度上,采用平均分割时间tavg,先计算视频中所有帧连续分割的时间,再平均即可得到每一帧鼠兔图像分割时间,所得结果如表1所示.

表1 三种方法的性能比较Table 1 The function comparison of three methods
通过对包含80 帧的鼠兔视频进行分割处理,从分割精度、算法复杂度对三种方法进行了对比分析,得出本文方法的平均相似度达到76%,远高于LBF模型的15%和RSF 模型的10%,且本文方法所需的平均分割时间tavg仅需要0.35 秒,比LBF 模型和RSF模型消耗的时间要少.
4 结语
根据高原鼠兔视频序列图像对比度较低及鼠兔目标运动突变性的特点,提出一种适合视频序列图像特点的时空联合分割方法,首先采用本文提出的快速目标检测方法获取运动目标的初始区域,再利用改进的LBF模型在得到的初始活动轮廓曲线上迭代演化. 实验结果表明:通过对包含80 帧的鼠兔视频进行处理,本文提出的方法总共消耗28.02 秒,平均每一帧序列图像耗时约为0.35 秒,平均相似度高达76%,与传统方法相比,在分割精度及算法复杂度上,本文提出的应用于鼠兔视频序列的分割方法都优于其它两种方法,为后续建立高原鼠兔的形态与行为学系统模型奠定了良好的基础.

