裂纹几何配置对裂隙砂岩力学特性及破坏模式的影响

田茂祥 雷瑞德 张 亮 陈小平 王 丰

（1.重庆市市政设计研究院，重庆400020；2.重庆大学资源与安全学院，重庆400044；3.重庆大学土木工程学院，重庆400045）

岩体中常常含有大量的缺陷，比如孔隙、裂隙及节理等。这些不连续体通常是由地质构造、长期风化及人类开挖活动形成的［1-3］。岩体中裂隙结构的存在很大程度上降低了岩体的整体力学强度，此外，地下工程开挖、隧道建设和矿山巷道支护等常常涉及裂纹断裂萌生、扩展及贯通过程［4-5］。因此，对裂隙岩石断裂演化过程进行表征和预测是非常必要的。

国内外学者对裂隙岩石的力学特性及断裂机制进行了大量的研究，并从中取得了诸多的研究成果［6-10］。在室内试验方面，Wong和 Einstein［6］采用石膏预制的单裂纹试样进行单轴压缩试验，得到翼型裂纹和次生裂纹的扩展演化特征。Yang和Jing［7］实施了单裂缝砂岩的单轴压缩试验，发现其力学参数与裂隙倾角具有一定的相关性。对于室内物理试验来说，试样在切割钻取过程中产生的初始损伤是很难定量表征，尤其预制裂隙岩样大多数是通过高压水刀加工切割，造成试样局部的初始损伤更大，从而得到的试验结果离散性较大。再加上物理试验很难定量地捕捉和表征裂纹的细观演化过程。除了室内试验外，众多学者借助数值模拟的方法对不同材料的裂纹扩展演化过程和贯通机制进行研究［11-13］。比如，Zhang和 Wong［11］采用离散元数值模拟方法研究单裂纹类岩石材料的强度、变形及断裂扩展过程，并总结了多种裂纹类型和岩桥贯通模式。然而，该研究未考虑多裂纹工况下裂隙岩石的断裂失稳机制。王桂林等［12］基于PFC2D软件对Z型裂隙砂岩的强度和断裂行为进行了详细的分析。得到裂纹的起裂应力水平在0.6～0.7之间，此外，还分析了不同裂纹的破坏模式。然而，该研究未考虑非贯通岩桥对裂隙岩石断裂行为的影响。截止目前，大多数研究者只考虑了单一裂隙因素，例如裂隙倾角或岩桥倾角对断裂机制的影响［14-16］。然而，实际工程中裂隙岩体的失稳破坏通常是由多个裂隙因素耦合作用诱发的。鉴于此，本项目对不同裂隙倾角和岩桥倾角裂隙砂岩的断裂破坏过程进行了一系列的模拟研究。

本研究以郑万高铁专线雷家坡隧道局部掌子面裂纹萌生扩展为背景，采用数值模拟反演方法分析不同裂隙几何结构下裂纹的扩展演化过程及强度特性，为隧道施工过程中遇到类似情况提供一定的指导借鉴意义，从而采取相应的止裂和支护加固措施。

1 工程背景

郑州至万州客运专线铁路（重庆段）站前工程ZWCQZQ-8标段起讫里程为DK806+949.06～DK819+278.697，标段正线全长12.329 km，其中隧道2座，总延长12.024 km，占正线长97.5%。标段内2座隧道均为长隧道，属于中度风险，其中雷家坡隧道为标段重难点工程，全长8 033 m，隧道最大埋深376 m，位于重庆市万州区大周镇与熊家镇境内。

雷家坡隧道于2016年7月21日开工，截止目前进口上台阶开挖1 114 m、二衬浇筑948 m，斜井上台阶开挖946 m、二衬浇筑767 m，出口上台阶开挖781 m、二衬浇筑660 m；天城隧道于2016年6月7日开工，目前进口上台阶开挖875 m、二衬浇筑756 m，出口上台阶开挖1 192 m、二衬浇筑1 044 m。从现场实测记录得知，隧道施工工程中伴随有不同宽度和深度的裂隙产生，其中12%裂纹宽度在0.2 mm以下，35%裂纹宽度0.2～0.5 mm，53%裂纹宽度0.5～1.5 mm。隧道的某个掌子面见图1。

2 数值试验方案

2.1 平行黏结模型原理

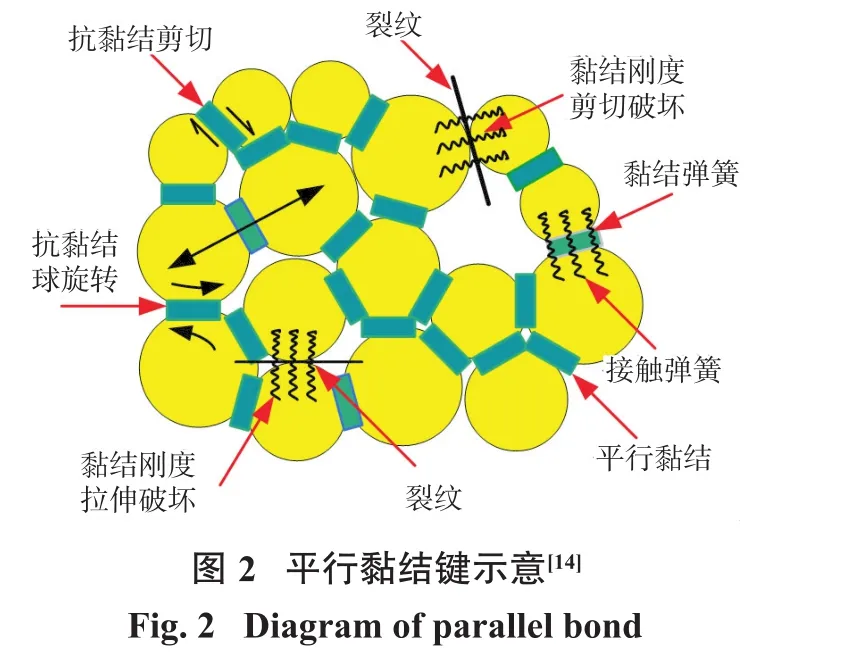
本研究采用PFC2D数值模拟软件，结合平行黏结模型（BPM）模拟颗粒间运动与变形的力学行为，该软件的计算原理基于牛顿第二定律。由于平行黏结键不仅能够在颗粒之间传递力和向量，而且能够传递接触点处的作用力。因此，平行黏结模型用于本研究模拟裂隙砂岩的力学强度和断裂行为。平行键模型示意图如图2所示［13］。

PFC2D模型中，应力是通过作用在每个颗粒上的平行黏结力与接触的方法获得，平均应力向量的计算公式［17］：

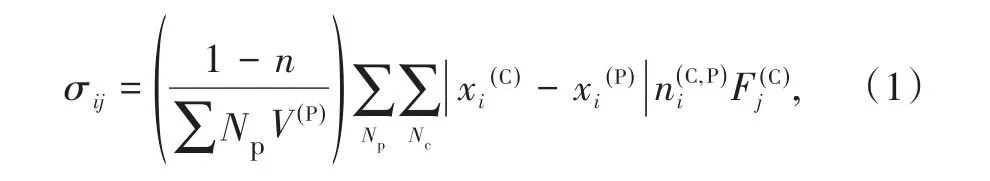
式中，Np为球的质心；Nc为球的接触；V()P为颗粒体积；n为孔隙度；和分别为颗粒质心和接触的位置；为接触的单位法向量；为接触作用力。

2.2 参数标定

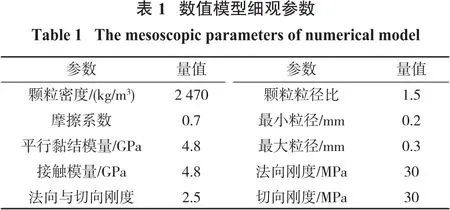
基于PFC2D数值模拟软件建立75 mm×150 mm（宽×高）二维离散元数值模型，颗粒直径在0.2～0.3 mm之间，颗粒总数为50 705个，颗粒之间的接触个数为132 439。首先，基于物理试验结果确定模型的细观参数，然后，采用反复调试的方法，得到最终模拟所需的细观参数。数值模型细观参数如表1所示。此外，为确保整个加载过程为准静态加载，墙体加载速率为 0.05 m/s［12］。

2.3 数值模拟方案设计

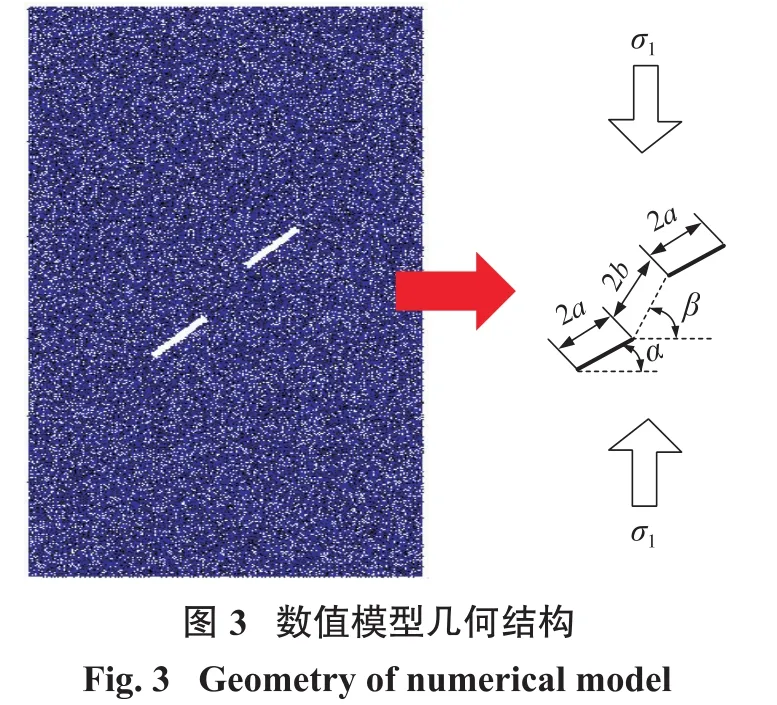
典型的数值计算模型几何结构如图3所示。预制裂纹长度2a为14 mm，岩桥长度2b为16 mm，裂纹宽度为1.5 mm。详细模拟方案为：①预制裂隙倾角α固定不变，岩桥倾角β依次为0°、30°、60°、90°、120°和150°；②岩桥倾角β固定不变，裂隙倾角α依次为15°、45°和75°。

3 裂隙砂岩强度及变形特征

3.1 应力—应变曲线

图4（a）、（b）、（c）分别为裂隙倾角15°、45°、75°时轴向应力—应变曲线。

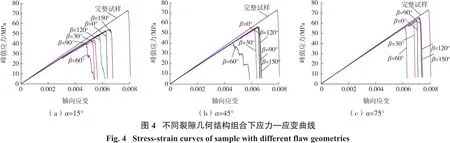
从图4得知，与完整试样的应力—应变曲线相比，含预制裂隙试样的应力—应变曲线均位于其下方。此外，试样在应力峰前和峰后均出现不同程度的波动现象，而完整试样的应力—应变曲线未出现该现象。该现象的主要原因是由于含预制裂隙试样在加载过程中裂纹尖端易形成高应力积聚区，而且矿岩体属于非均质材料。当加载作用力超过其最大拉伸应力时，导致试样局部破断失稳。随着加载的继续，新的承载体出现，从而使试样的承载能力再次增加。从图中还可得知，完整试样的峰值应力和峰值应变均高于裂隙试样。

3.2 强度和变形特征

通过获得不同裂隙工况下应力—应变曲线中应力的最大值，得到不同裂隙几何结构组合下峰值应力变化规律如图5所示。

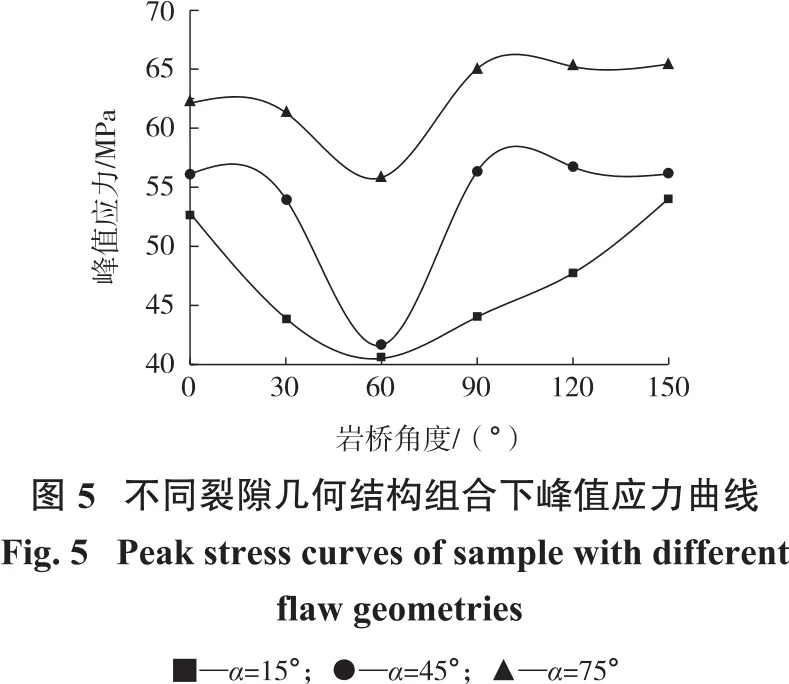
由图5可知，砂岩试样的峰值应力与裂隙倾角和岩桥倾角密切相关。总体来说，随着岩桥倾角的增加，峰值应力呈现出先降低后增加的变化趋势。此外，当岩桥倾角为60°时，峰值应力达到最小值。该现象的主要原因为常规岩石单轴压缩时剪切破裂角为45°+φ/2，并且该岩样的内摩擦角为34°，因此，该试样的剪切破裂角为62°。再加上试样预制裂纹的存在，裂纹尖端形成局部高应力积聚区。该区域的裂纹扩展速度要高于其他区域，导致裂隙尖端裂纹最先发育。

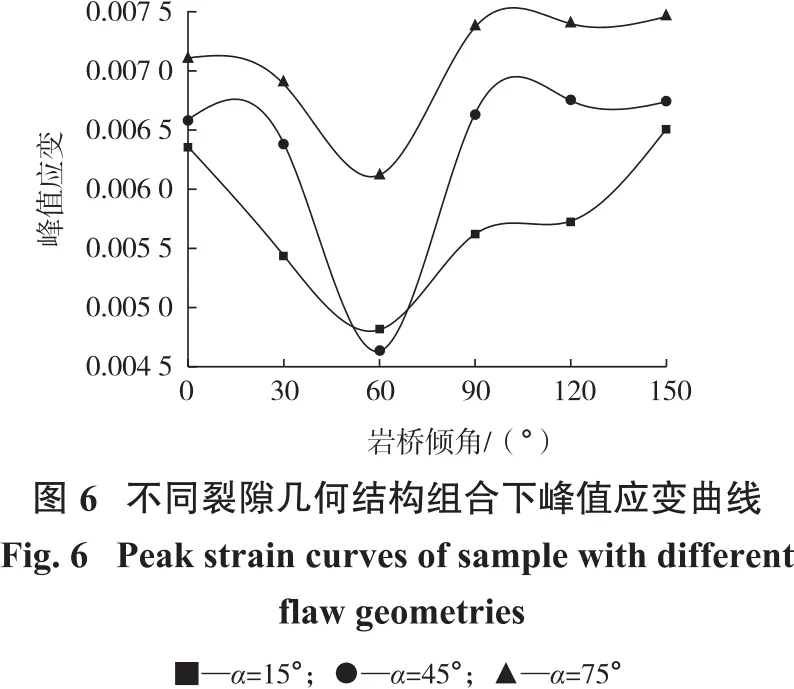
同时，不同裂隙倾角组合下峰值应力对应的峰值应变如图6所示。

由图6可知，峰值应变的变化趋势与峰值应力相似。随着岩桥倾角的增加，峰值应变呈现出先降低后增加的变化趋势。同一裂隙倾角下，岩桥倾角为60°时，峰值应变取得最小值。对应的最小峰值应变分别为0.004 81，0.004 63和0.006 12。

3.3 应变能演化规律

通过调用PFC2D软件中应变能计算命令，得到整个加载过程中试样应变能的演化规律，不同裂隙几何结构组合下应变能演化规律如图7所示。

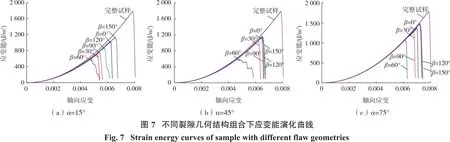
由图7可知，初始加载阶段，不同裂隙几何结构组合下应变能呈现出向下凹的非线性变化趋势。该现象的主要原因为试样内含有大量的初始孔隙、微裂隙等，由于孔隙、微裂隙的闭合，加载初期较小的作用力会产生较大的变形量。此外，完整试样的应变能均大于不同裂隙几何结构下的应变能。由于应变能的计算原理是基于应力—应变曲线所围成面积的积分，因此，从应力—应变曲线图中可以定性地获得应变能的大小。与试样的应力—应变曲线相对应，3种不同裂隙倾角下应变能最小值均在岩桥倾角为60°时获得。另外，从图中还可得知裂隙倾角为45°时，不同岩桥倾角的应变能演化规律接近。

3.4 阻尼耗散能演化规律

众所周知，当物体的弹性变形超过极限变形无法回到原始状态时，会导致机械能的损失，尤其当物体产生裂纹时，会有大部分能量消耗。因此，分析试样的阻尼耗散能有助于理解其断裂破坏机制。不同裂隙几何结构组合下阻尼耗散能演化规律如图8所示。

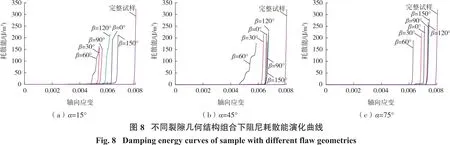
从图8可以看出，整个加载过程中，阻尼耗散能仅当试样趋近破坏时才开始出现，尤其在试样破裂的瞬间，阻尼耗散能急剧增加。从图中还可得知，随着预制裂隙倾角的增加，不同岩桥倾角对应的阻尼耗散能逐渐增大。

3.5 滑移摩擦能演化规律

滑移摩擦能是表征试样加载过程中产生裂纹时所消耗的能量，该参数能够间接地反应加载过程中裂纹数量的大小程度。不同裂隙几何结构组合下阻尼耗散能演化规律如图9所示。

从裂纹滑移摩擦能与轴向应变演化曲线得知，当试样进入屈服阶段后，其裂纹滑移摩擦能逐渐出现，随着变形的增加，裂纹滑移摩擦能逐渐增大。当曲线接近峰值应力时，裂纹滑移摩擦能呈直线趋势上升，并且裂纹滑移摩擦能随着裂隙倾角的增加而增加。

4 裂隙砂岩裂纹扩展特征分析

由于室内试验只能借助高速相机摄像技术捕捉某个时刻试样的宏观裂纹特征，而对试样内部细观微裂纹无法定量获取。从细观机理上分析岩石的损伤演化有助于更全面地理解岩石的宏观断裂失稳机制。而PFC2D数值模拟能够定量地表征整个加载过程中宏细观裂纹产生的位置及数量，因此，采用数值模拟方法对裂隙试样的损伤断裂演化过程进行表征显得非常必要。

4.1 裂纹扩展演化过程分析

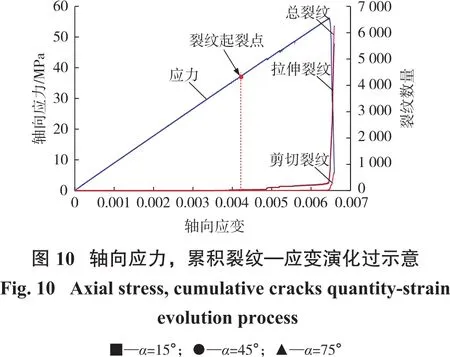
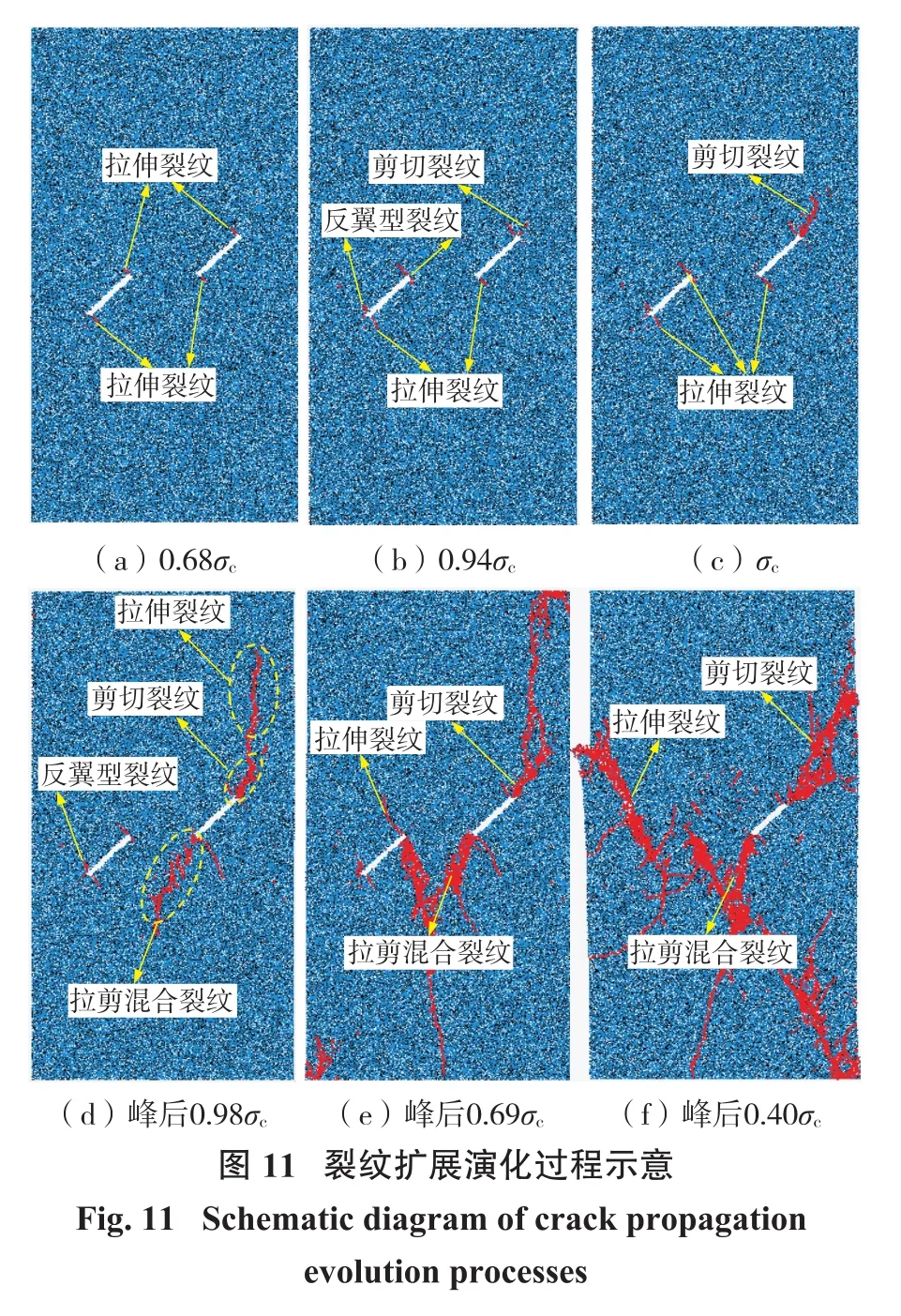
为了分析岩体内部微裂纹与宏观应力—应变曲线之间的对应关系，限于篇幅，本小节选取一组典型试样的裂纹演化过程进行分析。轴向应力、累积总裂纹、拉伸裂纹和剪切裂纹—应变的演化规律如图10所示。不同应力时刻对应的裂纹起裂、扩展和贯通演化过程如图11所示。

从图10可以看出，拉伸裂纹先于剪切裂纹出现，加载前期，未出现任何类型的裂纹，当荷载增至峰值应力的0.68σc时，拉伸裂纹开始缓慢地增加，直到接近峰值应力，剪切裂纹才出现。此外，整个加载过程中，拉伸裂纹起到了非常重要的角色，拉伸裂纹占总裂纹的89.08%。

从图11可以看出，裂纹的萌生位置出现在预制裂隙尖端，并以拉伸裂纹的形式出现。该现象主要是由于试样内晶粒位错和断裂等微损伤产生的。通过对比图10和图11，发现试样的宏观断裂过程与其微裂纹—应变曲线一一对应。随着荷载的增加，宏观裂纹的扩展长度逐渐增大，新的剪切裂纹沿着预制裂隙的方向扩展。当加载至峰值应力时，上预制裂隙右端剪切裂纹的扩展程度相对于拉伸裂纹较大，当应力降至峰后0.98σc时，上预制裂隙左端剪切裂纹开始扩展。随着变形继续增加，岩桥区域被拉伸裂纹和剪切裂纹连接贯通。当应力降至峰后0.40σc时，裂纹的数量及扩展程度进一步增加，宏观裂纹贯穿整个试样。

4.2 岩桥贯通模式分析

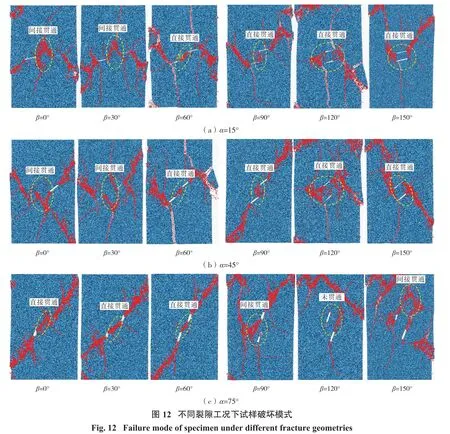
图12（a）、（b）、（c）分别为裂隙倾角 15°、45°、75°试样破坏模式示意图。基于Wong等［6］对裂纹类型的分类，主要有拉伸裂纹、剪切裂纹和拉剪混合裂纹等。

从图12（a）、（b）可知，试样的破坏模式由拉剪复合向剪切过渡再向拉剪复合模式转换。该破坏模式能够间接地解释图5中试样峰值应力的变化趋势。裂纹的起裂位置发生在预制裂隙尖端，并且试样的断裂区域主要集中在岩桥区域，试样的破坏模式主要为拉剪复合形式。随着岩桥角度的增加，岩桥贯通模式由间接贯通逐渐转化为直接贯通。

由图 12（c）可知，当岩桥倾角小于 120°时，试样的破坏模式为沿着预制裂隙形成的一条剪切断裂带。由此可推断，当裂隙倾角增至一定程度时，诱发试样断裂失稳的裂纹类型中剪切裂纹占比例逐渐增加。该现象也能够解释裂隙倾角与其对应的峰值应力之间的联系。此外，岩桥贯通模式不同于15°和45°工况，贯通模式由直接贯通变为间接贯通。

5 裂隙砂岩断裂锁固体理论讨论

众所周知，矿岩体属于非均质性较高的材料，其生成条件、矿物组分、胶结程度的不同会造成岩样内部强度不均，对于不同尺度的结构体，强度较大部分控制着整个试样的稳定性［18-19］。因此，从锁固体理论分析裂隙砂岩的断裂失稳过程即为其内部锁固体不断失稳破坏的过程。基于阿累尼乌斯方程得到砂岩的微破裂速度公式［20］:

式中，v为裂纹断裂速率；A0、A1为常数；T为岩体温度；k为玻尔兹曼常数；U0为断裂活化能；ε·为应变率；E为弹性模量。

为了计算方便，假设岩体加载过程为恒温过程，且加载速率为定值，则不同时刻t的累积微裂数［20］为

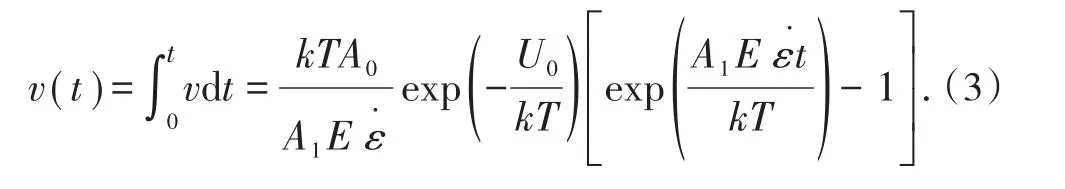
由式（3）可知，累积微裂数呈指数函数增加，结合图10分析发现，模拟加载过程中，试样累积微裂数—应变曲线的演化也呈现出指数函数增加。该公式从理论上也能够解释图11中的现象，由于预制裂隙附近锁固体较其他区域先发育，因此，岩桥锁固体区域最先失稳破坏，导致试样断裂区域裂纹扩展速度大于其他区域。

6 结论

（1）对比完整试样的应力—应变曲线特征，含裂隙试样的应力—应变曲线在峰值附近出现不同程度的波动，另外，裂隙试样的峰值应力和峰值应变均出现不同程度的降低。峰值应力和峰值应变的变化规律一致，当裂隙倾角不变时，二者随着岩桥角度的增加呈现出先降低后增加的趋势。当岩桥角度不变时，二者随着裂隙倾角的增加而增加。

（2）裂隙砂岩的应变能、阻尼耗散能和滑移摩擦能与裂隙的几何结构配置有关，均在岩桥倾角为60°时取得最小值。此外，阻尼耗散能从应力接近峰值时开始出现，裂纹滑移摩擦能从弹性阶段逐渐增加，尤其在接近峰值处急剧增加。

（3）当试样预制裂隙倾角为15°和45°时，随着岩桥角度的增加，岩桥贯通模式由间接贯通向直接贯通转换。但当裂隙倾角为75°时，随着岩桥角度的增加，岩桥贯通模式由直接贯通变为间接贯通。

（4）通过理论分析和模拟结果对比发现，加载过程中试样累积微裂纹随时间演化均呈现指数函数的形式。