问题2510的另证及推广

陕西省岐山县蔡家坡高级中学

1 前言

题目(《数学通报》2019年10月号问题2510[1])已知a,b,c＞1,a+b+c+2≥abc,求证：

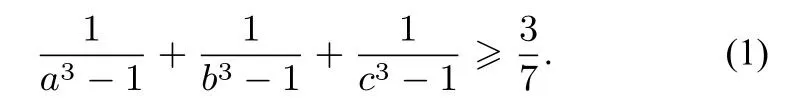
文[2]的作者在《数学通报》2019年11期给出了如下的

证明条件等价于即

注意到，当a≥b≥c＞1,时，有于是，应用切比雪夫不等式，得

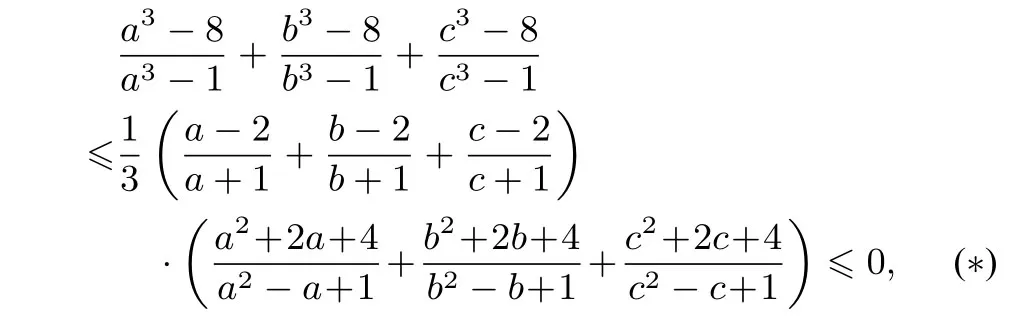
文[2]的证明中，不等式(∗)跳跃性太大，它不是由切比雪夫不等式直接得到的.按文[2]的证明，由切比雪夫不等式得到的不等式应该为：

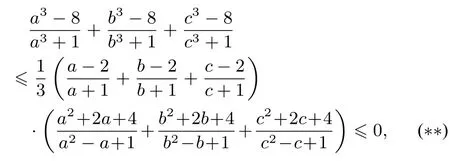
而由不等式(∗∗)要推出不等式(∗)，并不是显然的，还应该有适当的证明.下面的另证，调整思路，两次应用切比雪夫不等式，严格的证明问题2510.

2 另证

证明由已知，

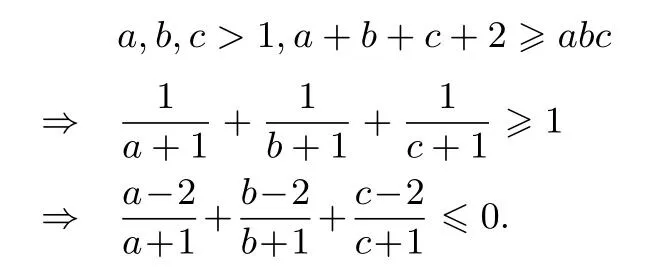
不妨设a≥b≥c＞1,先证明

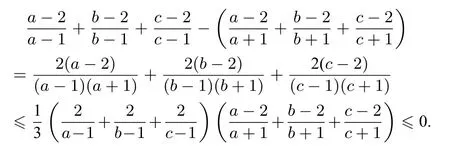
所以，

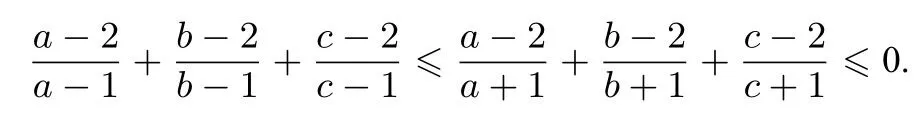
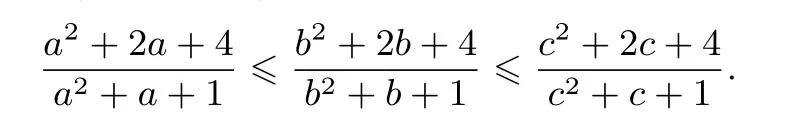
由切比雪夫不等式，得

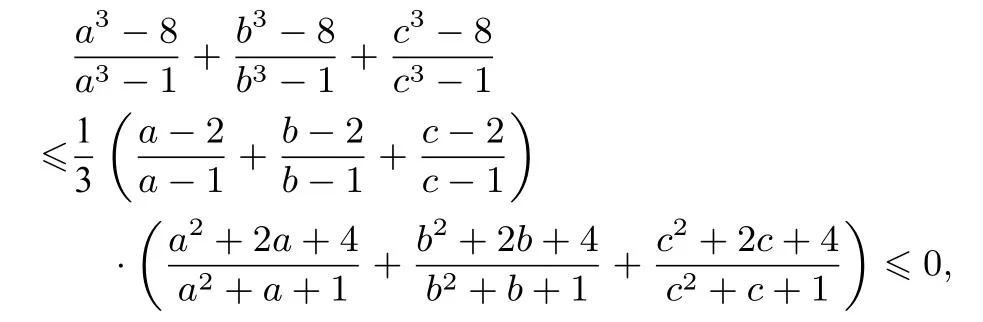
所以

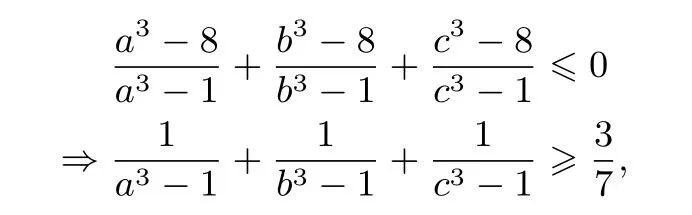
即不等式(1)成立.

3 推广

已知条件a,b,c＞1,a+b+c+2≥abc可推广为：ai＞1(i=1,2,...,n,n≥3,n ∈N),

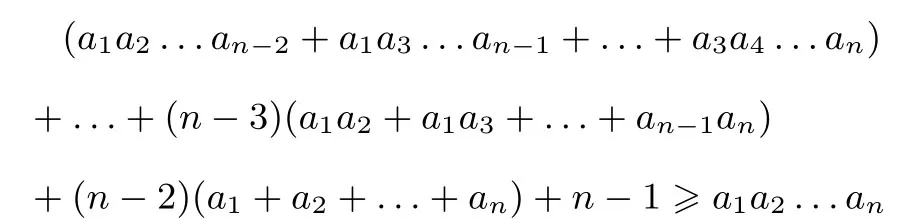
比较复杂，用起来也不方便.而

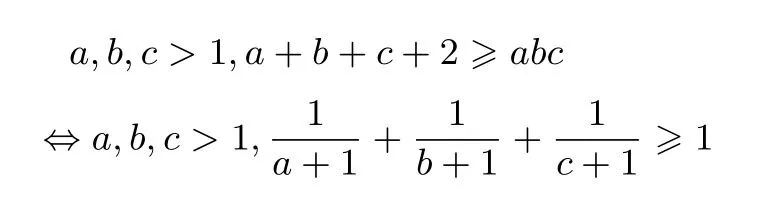
并且这个等价条件易于推广，使用方便，因此，可以考虑用等价条件作为已知条件进行推广.按照这个思路，下面对问题2510进行推广.

3.1 问题2510 按项数推广

定理1已知ai＞1(i=1,2,...,n,n≥3,n ∈则

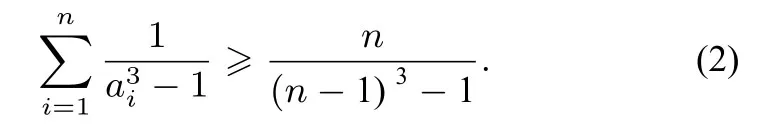
证明由先证明不妨设a1≥a2≥...≥an＞1,由有则而由切比雪夫不等式，得

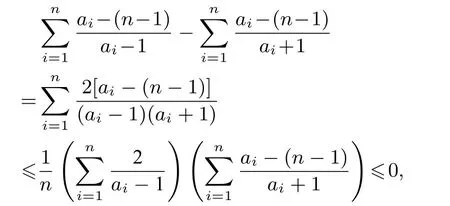
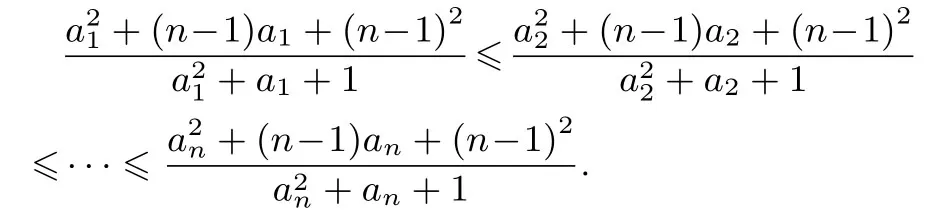
由切比雪夫不等式，得

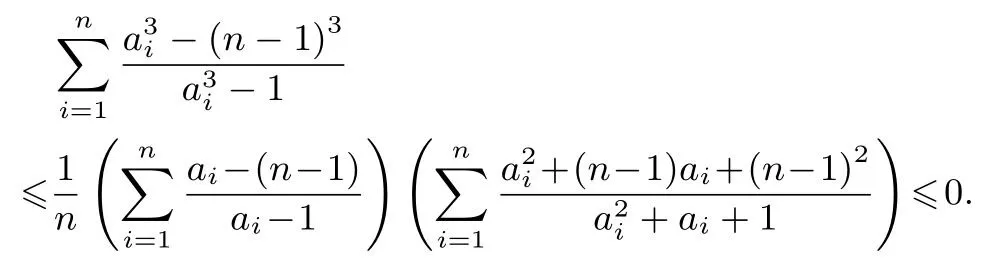
定理2已知ai＞k(i=1,2,···,n,n≥3,n ∈N,0＜k＜则

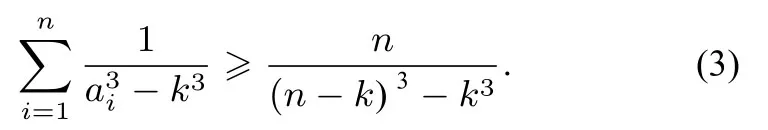
证明由先证明不妨设a1≥a2≥...≥an＞k,由有则

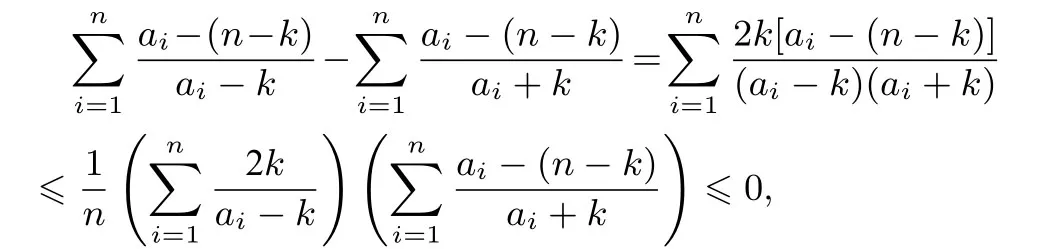
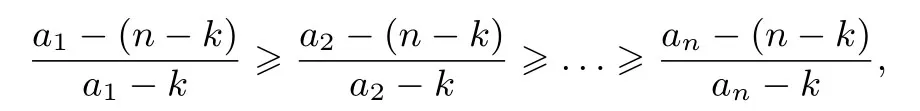
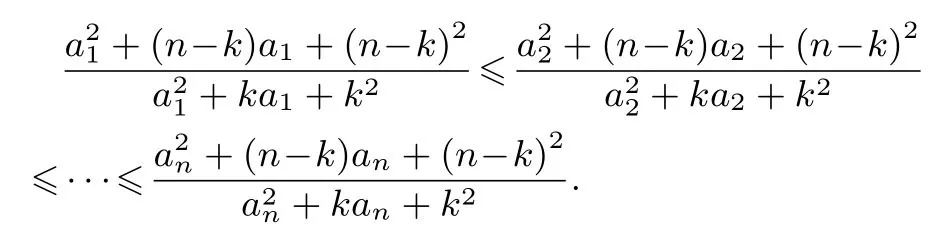
由切比雪夫不等式，得

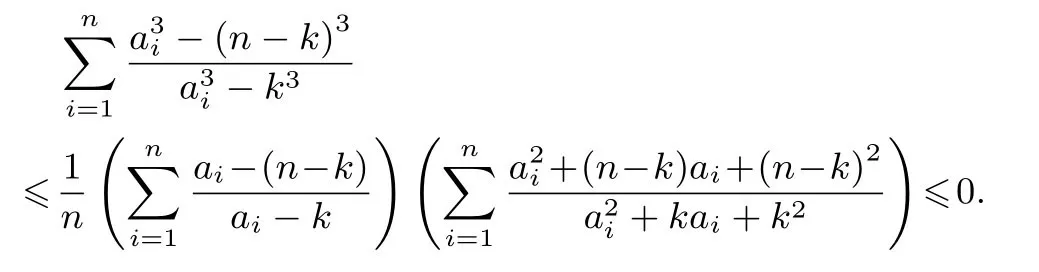
所以

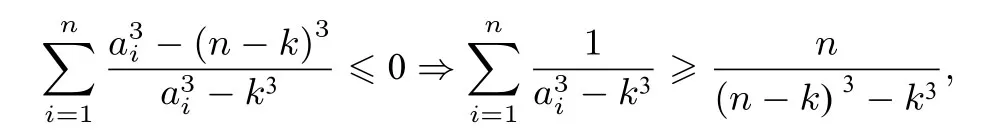
即不等式(3)成立.

3.2 问题2510 按指数推广

定理3已知ai＞1(i=1,2,...,n,n≥3,n ∈N),m≥则

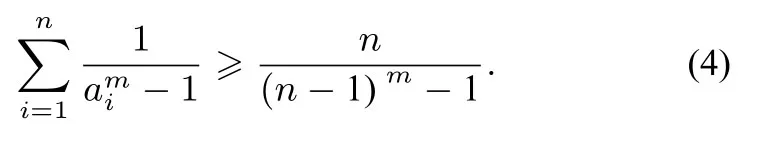
定理4已知ai＞k(i=1,2,...,n,n≥3,n ∈N,0＜则

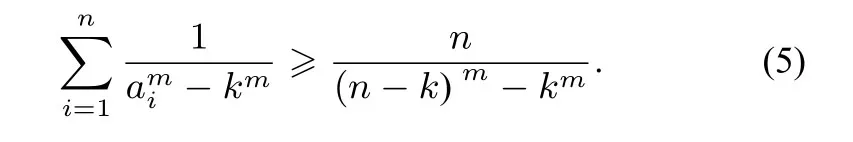
为证明定理3、定理4，先证明下面的引理：

引理已知h,k＞0,r,m ∈N+,r≤m,x＞0,则

(i)当h＞k时，函数

y=是减函数；

(ii)当h＜k时，函数

y=是增函数.

证明设则

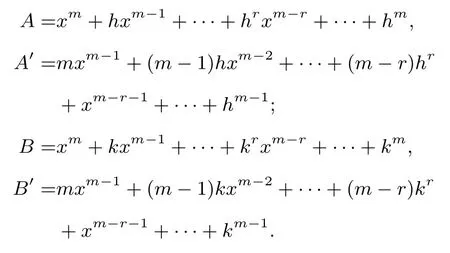
A′B展开式同次排成一列，得菱形状图表.

x2m-r-1项的系数分布：

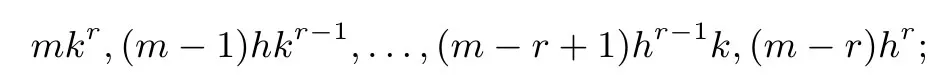
xm-r-1项的系数分布：

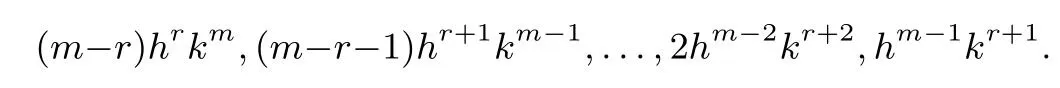
同理，AB′展开式中x2m-r-1项的系数分布：

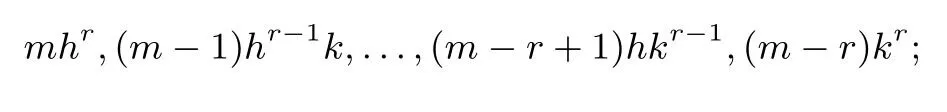
xm-r-1项的系数分布：

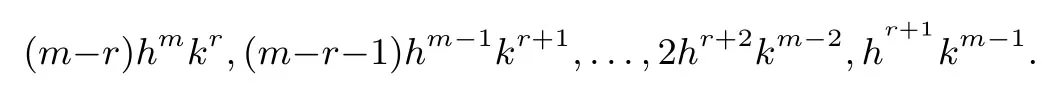
所以，得A′B-AB′展开式中两边(横、侧)的通项：故当h＞k时，y′≤0,函数

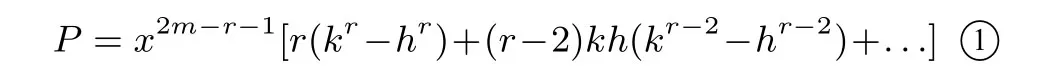
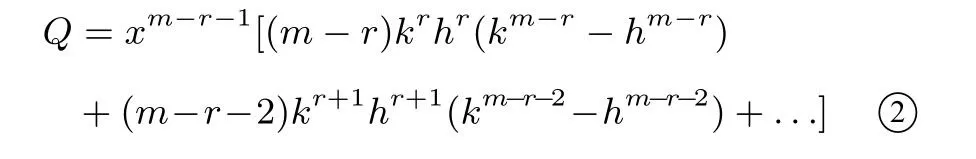
y=是减函数；当h＜k时，y′≥0,函数

y=是增函数.

验证r=1时，由①②分别得时，由①②分别得3时，由①得其和与上面计算的分子上的结果一致，并且，其增减性符合引理.

下面证明定理3、定理4：

证明由定理1的证明知且

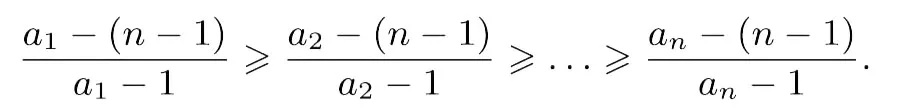
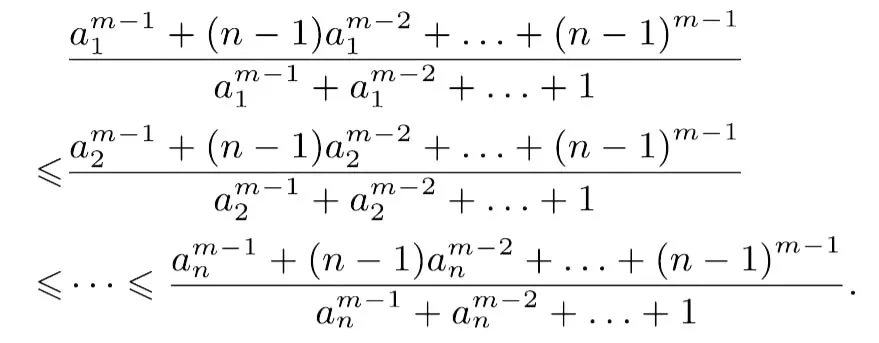
由切比雪夫不等式，得

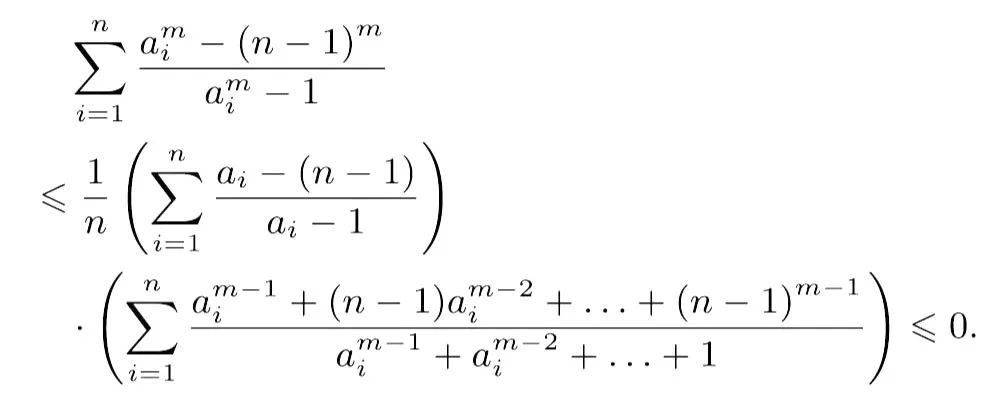
所以

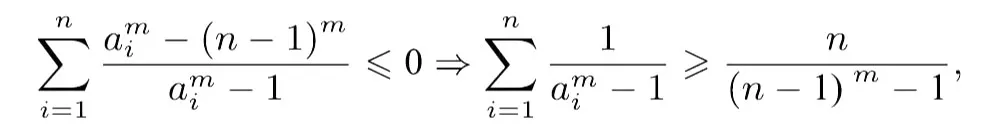
即不等式（4）成立.

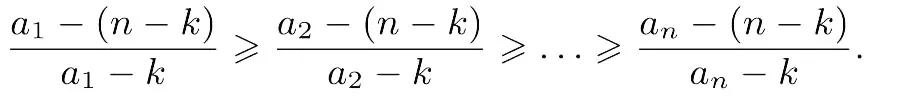
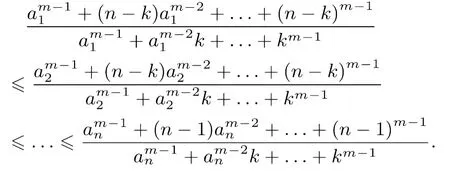
由切比雪夫不等式，得

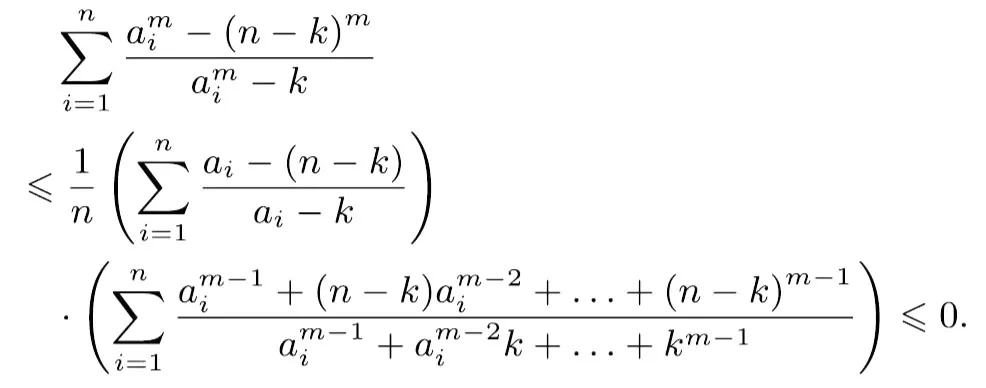
所以

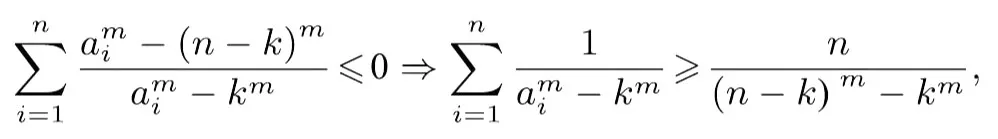
即不等式（5）成立.