证券买卖速度受制约下的最优交易策略*
林 辉, 杨 念*, 吴广谋
(1. 南京大学经济学院, 南京 210093; 2. 东南大学经济管理学院, 南京 211189)
0 引 言
现实中证券市场的供给与需求不是完全弹性的,故为保证交易的公平性,证券监管部门往往对投资者瞬间交易大额数量证券的行为实施限制,并为此制定了各种监管制度(1)例如,为防止市场操纵,上海证券交易所规定股票、基金、权证交易单笔申报最大数量应当不超过100万股,债券交易和债券质押式回购交易单笔申报最大数量不超过10万手..这些监管制度的实施,一方面使单个投资者无法操纵市场,以确保证券市场的有效性;另一方面,由于投资者的交易速度或持仓量受到制约,导致大额头寸无法瞬间出清,只能将其持有的头寸分割委托(split order),并在未来的若干时点上分别交易部分头寸以符合监管制度的要求.由此可见,若监管制度得到有效实施,投资者将面对一个弱式有效(weak-form)、交易速度或持仓量受到外生制度性约束的交易市场,那么,在这样的市场中投资者如何制定一个最优交易策略使其效用最大化?这正是本文的研究主题.
以往的研究成果忽略了外生制度性约束对交易策略施加的影响,隐含着投资者的持仓水平或交易速度完全由其自主择优决定的假设.明显地,若个别投资者执行这样的最优交易策略,可能给市场带来严重的冲击,甚至市场操纵.这与现实中投资者的交易行为受到监管制度约束的事实不符,也违背了有效市场的假设.为弥补以往研究的不足,本文将探讨交易速度受制约条件下的最优交易策略问题;其次,本文所研究不仅是证券的变现策略,而且对不同市场行情、任意初始持仓条件下的最优交易策略(既可能买入也可能卖出)都进行解析;最后,给出最优初始持仓,由此形成完整的最优交易策略.本研究使交易策略模型更贴近现实,具有重要的理论和实践意义.
1 相关文献回顾与评述
为了降低市场冲击(market impact)对交易价格的不利影响,持有大额头寸的交易者通常会将证券拆分为较小的份额分批出清,那么,在不确定性条件下,将证券分多少批次,以及每批次交易多少数量,以实现最大化的投资效用,便成为最优交易策略的核心问题.
基于执行成本(execution cost)或交易成本视角的最优交易策略模型.Bertsimas和Lo[1]研究了在给定期限内买入大量证券的预期成本最小化问题,提出所谓的最优执行(optimal execution)策略模型,但他们的模型不考虑执行(买入)成本的风险(波动性),隐含着投资者是风险中性的假设.Almgren和Chriss[2]基于均值-方差准则,在给定交易成本的方差条件下,以最小化交易成本的期望值来构建最优变现(optimal liquidation)策略模型,故Almgren-Chriss模型讨论的是证券的卖出问题.在此基础上,Almgren和Chriss还以最小化二阶效用函数或风险值(VaR)来分析最优变现策略,从而将Bertsimas和Lo的模型拓展到风险规避者.但上述两类模型得到的最优策略是静态的,即模型不依赖于交易期间证券价格的预期变化.Gatheral和Schied[3]基于几何布朗运动描述证券价格的变化过程,提出最优交易策略动态模型,从而对Almgren-Chriss模型进行拓展.其次,前人还以不同的方式刻画交易成本及其波动性.如Ting和Warachka等[4]以证券的卖出价格与其内在价值的偏差来刻画流动性折扣(liquidity discount),提出基于流动性折扣的最优变现策略模型.Caccioli等[5]以期望损失(excepted shortfall,ES)来衡量风险,基于最小化期望损失构建最优变现策略模型.Almgren[6]研究了流动性和波动率都随机变化条件下的最优变现策略问题.Subramanian[7]构建一个局部均衡模型,来讨论大额资产的投资者在有限或无限交易时间内的最优变现问题.此外,不同于执行成本最小化的视角,Pemy和Zhang等[8]以预期投资收益率最大化为目标构建最优变现策略模型.
基于定单簿(order book)视角的最优交易策略模型.Cheng等[9]基于订单被执行的不确定性对Almgren-Chriss模型进行了扩展,并在线性情形下获得最优策略的解析解.Obizhaeva和Wang[10]提出一个块状(block-shaped)限价定单簿(limit order book)模型研究了证券的跨期供求如何影响交易策略.研究表明:在交易时间给定条件下,市场弹性(resilience)是最优交易策略的关键因素.为放松Obizhaeva-Wang模型块状限价单簿的假设,Alfonsi和等[11]研究了限价单簿具有非均匀价格分布的模型.Predoiu和Shaikhet等[12]研究了具有任意形状的限价订单簿模型.Siu等[13]基于Obizhaeva-Wang模型,提出了由马尔科夫链刻画市场弹性的模型,并给出解析解.以上的模型都是基于买入指令讨论了最优策略问题,故缺乏对卖出策略的分析.Tsoukalas和Wang等[14]进一步把Obizhaeva-Wang模型拓展至多资产的情形,并指出不同资产之间的价格冲击对最优交易策略具有显著的影响.
国内学者也对最优交易策略开展了有价值的研究.仲黎明和刘海龙等[15]提出在给定风险条件下使期望利润最大化(期望损失最小化)的最优变现策略.林辉等[16]通过放松理想化市场的假设条件,构建流动性调整的最优交易策略模型,并给出解析解.唐衍伟和陈刚等[17]研究了单只股票与股指期货构建的套期保值组合不完全变现连续出清策略问题.邴涛等[18]基于指令驱动市场证券价格的形成过程,研究了非知情交易者的最优交易策略.
相比以往的最优交易策略模型,本文所提出的模型主要有以下不同之处:1)考虑了交易策略面临的外生制度性约束.以往的研究中交易速度完全由最优策略模型内生决定,故交易速度可以充分大,但这样的交易策略很可能因现实中的监管制度约束而无法实施,因为交易速度或持仓水平需受到监管约束的. 2)本文构建的最优交易策略是买入与卖出证券的混合策略,即在给定的投资期限内,投资者在卖出证券后还可以买入证券,或者在买入证券后还可以卖出.纵观以往的模型,要么是纯粹的变现策略,要么是纯粹的买入策略,缺乏对混合策略的研究.因此,本文在前人研究基础上的改进将使模型更贴近实际.
2 最优交易策略模型的构建
假设一个具有风险规避倾向(risk aversion)的投资者在初始时刻(t=0)拥有数量为x(0)=x0(下文简称“初始持仓”)的证券,需要在[0,T]期间完成交易,这里,T>0为投资期的终点时刻,设该时刻的目标持仓x(T)=xT≥0.投资者的交易策略是由其可控变量——交易速度v(t)或持仓x(t)构成(2)交易速度与持仓水平可以相互转化,故本文以交易速度或持仓水平来表示交易策略.,显然,t时刻投资者的持仓量为

(1)
为了防止市场操纵,证券市场一般都有最大申报数量之限制.一方面,它使投资者的交易速度受到约束,不妨设-v0≤v(t)≤v0,其中v0>0.另一方面,由于投资者的交易速度受到约束而不能操纵市场,其交易行为不能破坏证券市场的有效性,故可以假设投资者在一个弱式有效市场中进行交易.为简化表达证券市场的弱有效性,不妨以几何布朗运动来表示证券价格变化的随机过程,从而证券回报率可表示为
r(t)=a·t+ξ(t)
(2)
其中a≠0为漂移率,它表示投资者对证券未来走势的预期.若a>0,则表示投资者预期证券价格将上涨;反之,若a<0,则表示投资者预期证券价格将下跌.ξ(t)是一个维纳过程,当t2>t1时,有ξ(t2)-ξ(t1)~N(0,σ2(t2-t1)),这里σ为波动率,表示单位时间内的风险.
对于任意t∈[0,T],投资者可根据市场情况选择交易速度v(t),由此形成交易策略或交易轨迹(v(t),t∈[0,T]),显然交易策略的选择直接影响投资回报率.若投资者选择某个交易策略,则由式(1)和式(2)可知,在整个投资期[0,T]可获得的总回报率Π为

(3)
这里的v(t)dt构成瞬间交易额.
假设投资者以“给定风险的条件下,最大化总回报率期望值”准则来选择交易策略,不妨以均值-方差效用函数U(Π)来表示投资者获得的投资效用(3)如果不采用均值-方差效用函数,结果依然成立. 例如,采用绝对风险规避效用函数时,投资者效用仍可以用式(4)来表示,证明参见附录.,这里
(4)

(5)
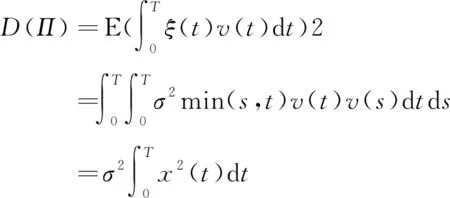
(6)
将式(5)和式(6)代入式(4),且将交易速度v(t)、初始持仓x(0)和期末持仓x(T)等列为约束条件,则交易速度受制约、市场弱有效条件下的最优交易策略问题可表示为

(7)
3 最优交易策略所有可能的解
本节采用极大值原理(maximum principle)来讨论最优交易策略问题.根据极大值原理,由式(7)可定义哈密尔顿(Hamilton)方程

(8)

(9)
且其约束条件为

(10)

(11)
其他约束条件还有:-v0≤v(t)≤v0、x(0)=x0和x(T)=xT.
由式(8)给出的哈密尔顿函数形式可知,交易速度v(t)的变化与共积变量λ(t)=0的时点有关,故下文将通过分析λ(t)=0的规律,来推导最优交易策略.为此,不妨设集合B={t|λ(t)=0,t∈[0,T]},并分3种情形探讨集合B与最优交易策略的关系,这些情形分别是:(1)集合B为空集;(2)集合B为单点集(只有1个元素);(3)集合B为非单点集、非空集(有2个或2个以上的元素).显然上述情形构成集合B的所有结果,所以,分别在上述3种情形下推导模型,就能得到最优交易策略所有可能的解析解.
3.1 集合B为空集下的交易策略
若B为空集,则表示在[0,T]区间上都有λ(t)>0或λ(t)<0,故最优交易策略可分为两种情形加以讨论:
(1)若λ(t)>0,∀t∈[0,T],则最优交易速度v*(t)=-v0<0,从而最优持仓为
x*(t)=x0+v0t,t∈[0,T]
(12)
且由式(12)可知初始持仓x0满足x0=xT-v0T.
(2)若λ(t)<0,∀t∈[0,T],则最优交易速度v*(t)=v0>0,则最优持仓为
x*(t)=x0-v0t,t∈[0,T]
(13)
且由式(13)可知初始持仓满足x0=xT+v0T.
3.2 集合B为单点集下的交易策略
若B为单点集,不妨设[0,T]区间上存在唯一的t0使得λ(t0)=0,且t0≠0,t0≠T,则根据λ(0)和λ(T)的取值可分为4种情形进行讨论:
(1)若λ(0)>0且λ(T)>0,则当t=t0时存在λ(t0)=0,此时最优交易速度v*(t)=-v0,从而最优持仓为x*(t)=x0+v0t,这与3.1节(1)中的策略相同,不再赘述.
(2)若λ(0)<0且λ(T)<0,则当t=t0时存在λ(t0)=0,此时最优交易速度v*(t)=v0,从而最优持仓为x*(t)=x0-v0t,这与3.1节(2)中的策略相同,不再赘述.
(3)若λ(0)>0且λ(T)<0,则当t=t0时存在λ(t0)=0,此时最优交易速度可分为两种情形:(a)v*(t)=-v0,t∈[0,t0);(b)v*(t)=v0,t∈[t0,T].这意味着投资者先以-v0的速度增加持仓,到t0时刻再以v0的速度减少持仓,故此种情形下的最优持仓为
(14)
将x(T)=xT代入式(14)即可得到
(15)
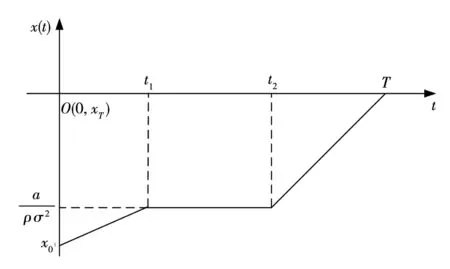
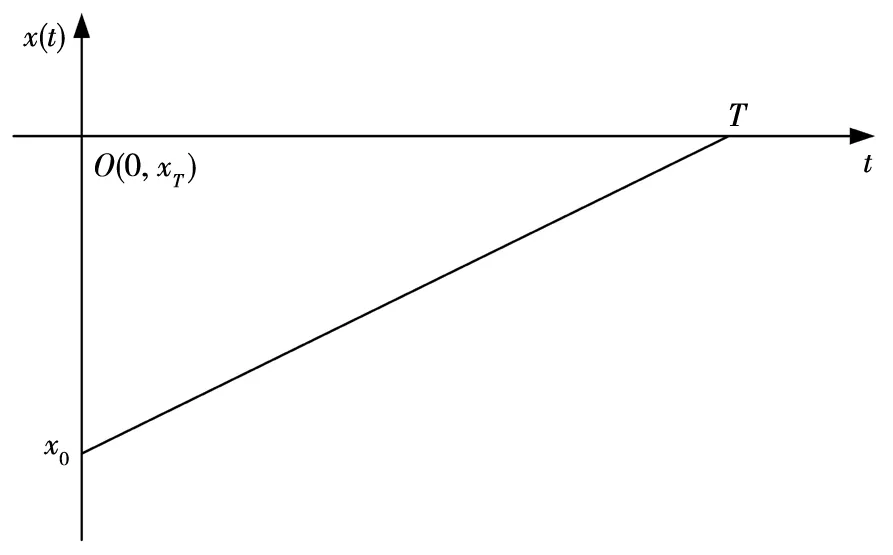
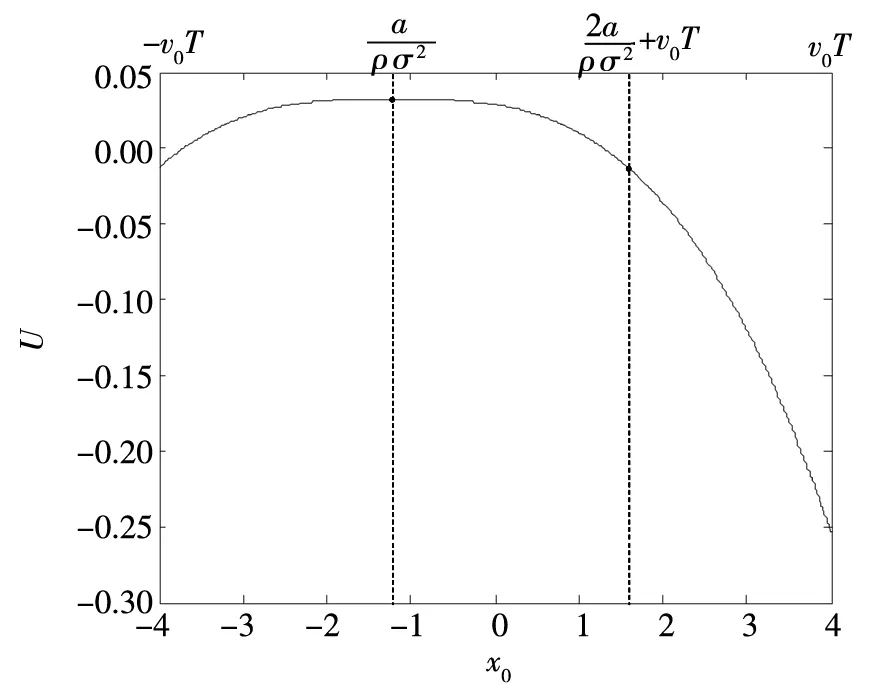
由于0 (4)若λ(0)<0且λ(T)>0,则当t=t0时存在λ(t0)=0,此时最优交易速度可分为两种情形:(a)v(t)=v0,t∈[0,t0);(b)v(t)=-v0,t∈[t0,T],这意味着投资者先以v0的速度减少持仓,到t0时刻再以-v0的速度增加持仓,从而该情形下的最优持仓为 (16) 将x(T)=xT代入式(16)即可得到 (17) 在给定的投资期[0,T]内,若集合B存在任意的2个不同元素ti和tj使得λ(ti)=λ(tj)=0,不妨设ti 证明令tl=max{t∈[ti,tj]:λ(t)=0}和tm=min{t∈[ti,tj]:λ(t)=0},即tl和tm分别是[ti,tj]区间上使得λ(t)=0的最大时点(最右边)和最小时点(最左边).明显地,当tl>tm,对于任意的t∈[ti,tj],都有λ(t)=0,则上述结论自然成立. 下面采用反证法证明:当tl>tm时,对于任意的tk∈[tm,tl],都有λ(tk)=0. (ii)假设λ(tk)<0,由λ(t)的连续性同理可知,λ(t)在区间N(tk,εi)上为凸函数,且由λ(tk-ε1)=λ(tk+ε2)=0推断λ(t)>0,t∈N(tk,εi),i=1,2,但这与该区间上λ(t)<0是矛盾的. 由(i)和(ii)的证明可知,对于任意的tk∈[tm,tl],都有λ(tk)=0,且由tl和tm的定义可知,显然有tm≤ti (18) 由式(18)可以得到最优持仓为 (19) (20) (2)若λ(0)>0、λ(T)>0,类似于3.3节(1)中的分析思路,容易求得此种情形下最优交易速度为 (21) 从而,最优持仓为 (22) (23) (3)若λ(0)>0、λ(T)<0,类似于3.3节(1)中的分析思路,同理可得最优交易速度为 (24) 且最优持仓为 (25) (26) (4)若λ(0)<0、λ(T)>0时,类似于3.3节(1)中的分析思路,同理可得最优交易速度为 (27) 且最优持仓为 (28) (29) 第3节基于共积变量λ(t)推导出最优交易策略所有可能的解析解,本节将根据该结果,进一步探讨投资者基于市场行情的预期及其初始持仓,从第3节给出的全部结果中挑选其最优交易策略. 当a>0,即投资者预期市场行情上涨,对照第3节的分析结果,可得到各种初始持仓下的最优交易策略: (1)若初始持仓x0>v0T+xT,由于交易速度受到约束,投资者即便以最大交易速度v0卖出证券,但在T时刻仍有超过xT持仓量.这说明,投资者因其持有多头仓位太多,即便以最大的交易速度卖出平仓,也无法在投资期限内将仓位减持到目标值xT,故该情形下最优交易策略无解(4)为了讨论的完备性,无解情形可视为最优交易策略的例外情形.. (2)若初始持仓x0=v0T+xT,即对应于3.1节(2)中的情形,故最优持仓由式(13)给出,其轨迹如图1所示.图中的O点的坐标为(0,xT),从图2到图10的坐标系同此,不再赘述. 图1 当a>0,x0=v0T+xT时最优持仓轨迹 图2 当时最优持仓轨迹 图3 当时最优持仓轨迹 图4 当时最优持仓轨迹 (6)当初始持仓x0=xT-v0T时,这对应于3.1节(1)中的情形,最优持仓由式(12)给出,其轨迹如图5所示. 图5 当a>0,x0=xT-v0T时最优持仓轨迹 (7)当初始持仓x0 当a<0,即投资者预期市场行情下跌,类似于4.1节中的分析思路,可以归纳出各种初始持仓情形下的最优交易策略. (1)若初始持仓x0>v0T+xT,由于市场行情是看跌的(a<0),故投资者需要以最大交易速度v0卖出证券,但由于初始持仓过大,导致其在终点时刻的持仓仍大于目标仓位xT,显然该情形下最优交易策略无解. (2)若初始持仓x0=v0T+xT时,最优持仓由式(13)给出,其轨迹如图6所示.不难发现,图6与图1是相同的,但图6所对应的市场行情却是看跌的(a<0).这说明:在投资期限[0,T]内,无论市场行情如何,若投资者需要出清的仓位达到市场所能允许的上限v0T,就只能以最大的交易速度v0向市场出清. 图6 a<0,x0=v0T+xT时最优持仓轨迹 图7 当时最优持仓轨迹 图8 当时最优持仓轨迹 图9 当时最优持仓轨迹 (6)当初始持仓x0=xT-v0T时,最优持仓由式(12)给出,其轨迹如图10所示. 图10 当a<0,x0=xT-v0T时最优持仓轨迹 (7)当初始持仓x0 (30) (31) 图11 行情看涨时不同初始持仓下的投资效用 其一阶导数为 (32) (33) 图12 行情看跌时不同初始持仓下的投资效用 图12中的参数设置是:目标仓位为xT=0,漂移率a为-0.15,其他参数的设置同5.1节,由图12可知,当行情看跌时,投资者的最大效用同样在机会容量处取得. 本文基于弱有效市场的假设,并对交易速度施加制度性约束,构建最大化投资效用的动态交易策略模型;运用极大值原理推导出最优交易策略所有可能的解析解,并在此基础上给出:不同市场情形、各种初始持仓条件下的最优交易策略.通过对上述策略的进一步分析可以发现: (1)在弱有效市场的条件下,存在一个使投资效用最大化的初始持仓,即机会容量.它由证券的预期回报率和波动率,以及投资者的风险规避系数三个因素决定.无论投资者的初始持仓大于还是小于机会容量,都会导致其投资效用的下降.只有当其持仓水平等于机会容量时,才能获得最大化的投资效用. (2)不论市场行情如何(看涨还是看跌),投资者需以最大交易速度在投资期的初始阶段以机会容量为目标调整持仓,并尽可能使其持仓水平达到机会容量,然后保留该持仓水平在投资期的最后阶段以最大交易速度出清头寸.这是弱有效市场、交易速度受制约条件下最优交易策略的共同特征.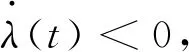

3.3 集合B为非单点集、 非空集下的交易策略

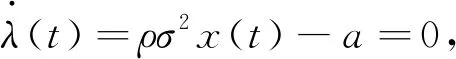


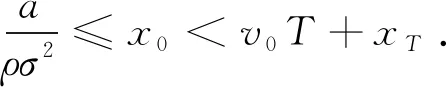

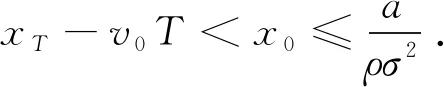
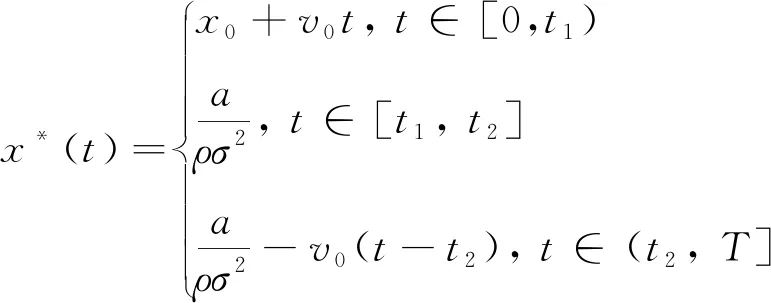


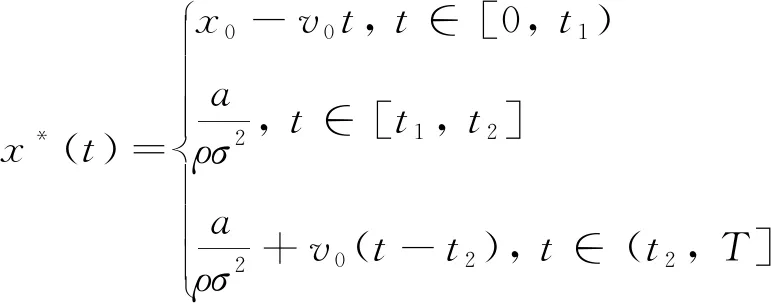
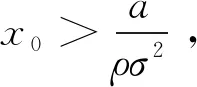

4 不同市场行情、 各种初始持仓条件下的最优交易策略
4.1 市场行情看涨时的最优交易策略

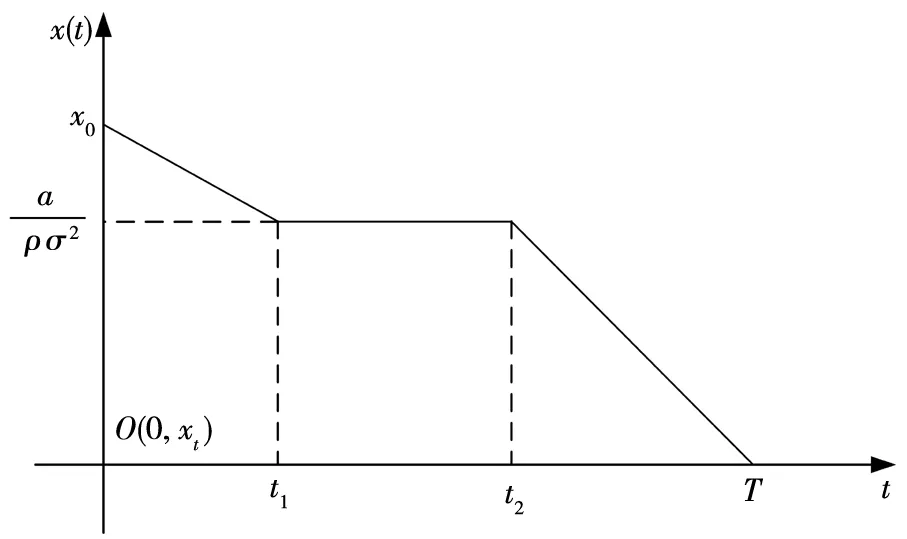
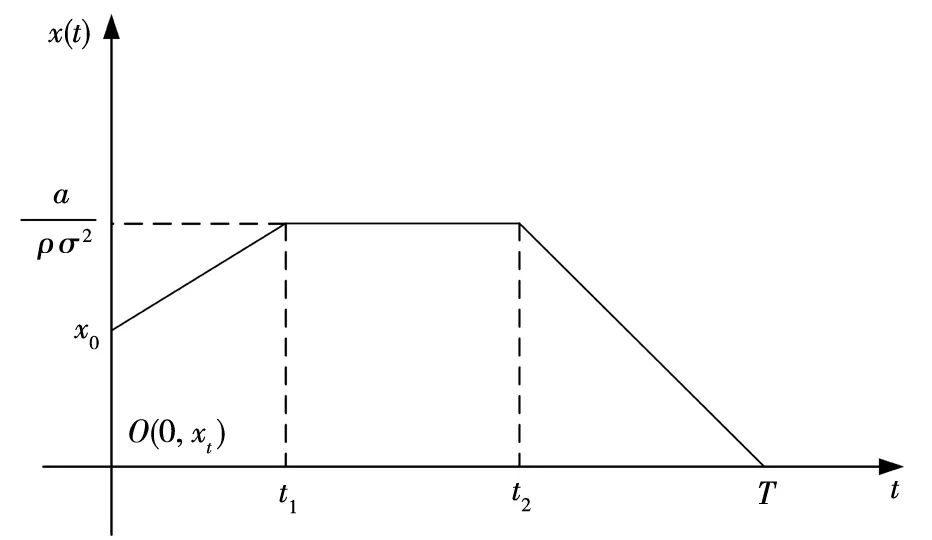


4.2 市场行情看跌时的最优交易策略
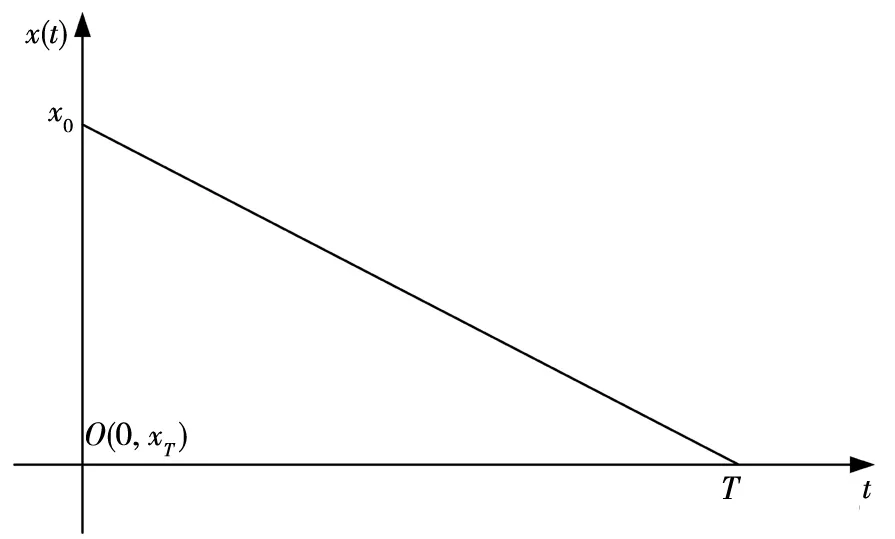
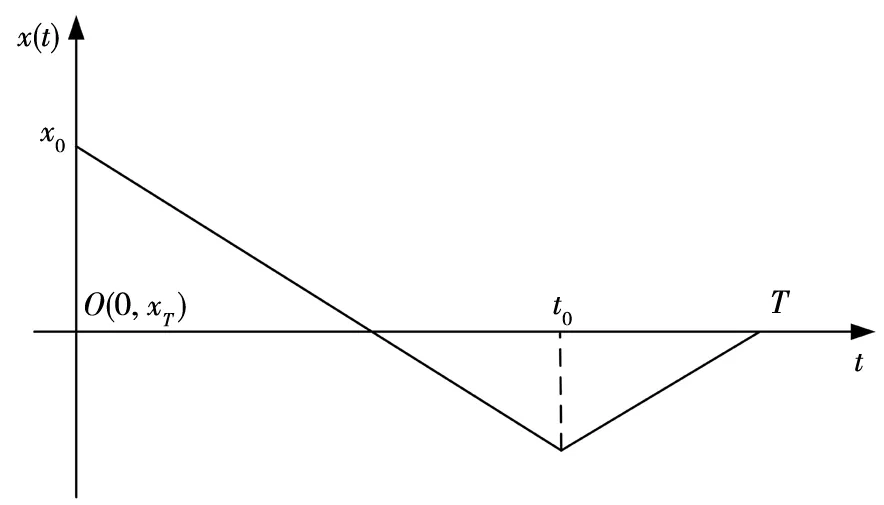

4.3 机会容量与市场容量
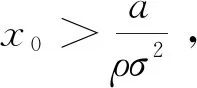
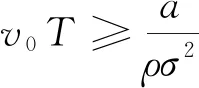
5 最大化投资效用的初始持仓
5.1 行情看涨时的最优初始持仓与最大化投资效用

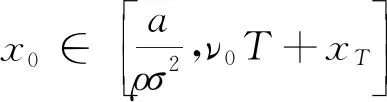
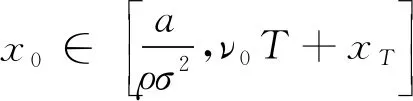

5.2 行情看跌时的最优初始持仓与最大化投资效用

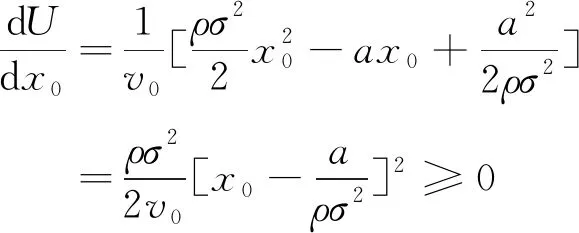

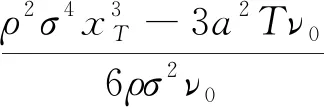
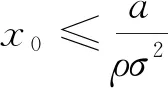
6 结束语

