保定市空气质量综合评价模型研究＊

冯 娟，冀 松，王 艳

（保定理工学院，河北 保定 071000）

保定市空气污染问题受到保定市政府的高度重视，近年来保定市政府一直致力于治理严重的空气污染。因AQI评价的6中污染物浓度限值各有不同，采用AQI评价空气质量，需要将不同污染物浓度限值折算成空气质量分指数AQI。当碰到严重污染天气时，AQI值就会超过500的最高限值，出现“爆表”现象，因此需要在AQI评价基础上进行改进。

1 空气质量指数

空气质量指数（AQI）是定量描述空气质量状况的无量纲指数，其数值越大、级别和类别越高说明空气污染状况越严重，对人体的健康危害也就越大[1]。针对单项污染物还规定了空气质量分指数。空气质量分指数（IAQI），是指根据单项污染物计算得出的空气质量指数。从各项污染物的IAQI中选择最大值确定为AQI，首要污染物即IAQI最大的污染物，当污染物浓度超过最高上限，就会发生“爆表”。

2 研究区数据

2.1 各污染物质量浓度

通过中国环境空气在线监测分析平台，收集保定市2018年全年每天空气质量监测指标数据[2]，因数据量庞大，仅附全年各污染物质量浓度月均值数据，见表1。从表1统计结果可以发现，空气污染季节性特征明显，每年的夏、秋季污染物质量浓度都较低，曲线呈“V”字型，最低值在夏季，而冬季到春季浓度值都较高，曲线呈倒“V”字型，最严重污染季节为冬季。

表1 2018年各污染物质量浓度月均值数据

2.2 因子分析

因子分析法是指从研究指标相关矩阵内部的依赖关系出发，把一些信息重叠、具有错综复杂关系的变量归结为少数几个不相关的综合因子的一种多元统计分析方法[2]。基本思想是：根据相关性大小把变量分组，使得同组内的变量之间相关性较高，但不同组的变量不相关或相关性较低，每组变量代表一个基本结构一即公共因子。

对空气中的主要污染物(细颗粒物(PM2.5)、可吸入颗粒物(PM1O)、一氧化碳(CO)、二氧化氮(NO2)和二氧化硫(SO2)和臭氧(O3)进行了因子分析。其中KMO的值为0.652，大于阈值0.5，说明变量之间是存在相关性；Bartlett球形检验的结果，Sig.这一项值为0.000，小于0.05，说明因子分析是有效的[3]。

公因子方差结果见表2。从表中可以看出，每一个变量提取值均大于0.7，说明每一个变量都可以用公因子表示。

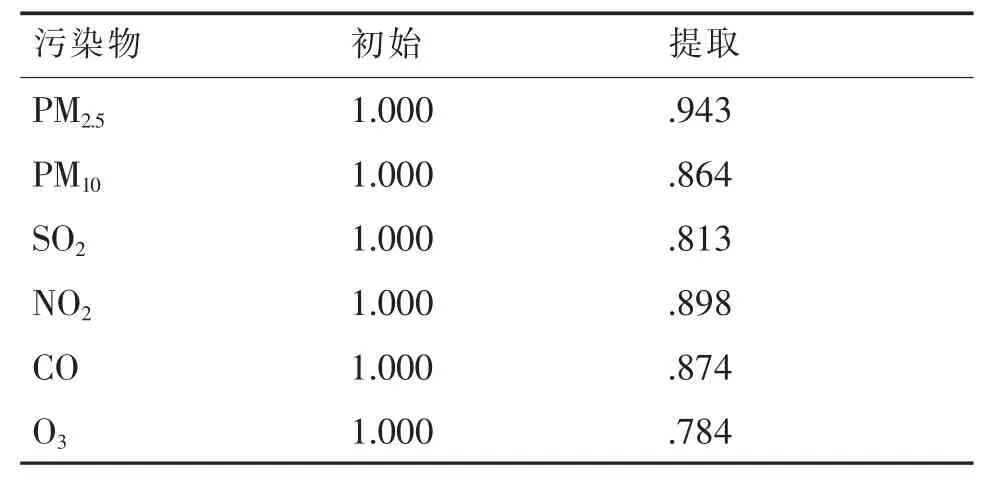
表2 公因子方差

解释的总方差结果见表3。解释的总方差代表因子对于变量解释的贡献率。从表中可以看出，选取三个代表因子就可以将变量表达到了97.60%。

表3 解释的总方差

成分矩阵见表4，得到三个综合评价因子。根据因子分析结果，也可以看出，空气污染的主要污染物为 PM2.5，NO2，CO。

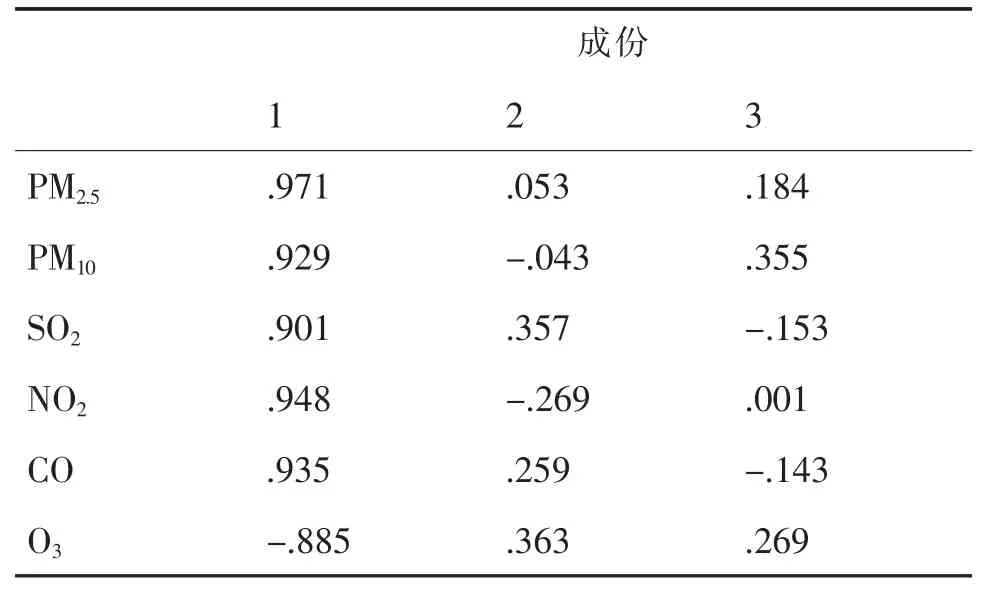
表4 成份矩阵

3 模型的建立

3.1 多元逐步回归分析

多元逐步回归分析方法[4,5]，首先建立因变量和自变量之间的总回归方程，再对总的方程及每一个自变量进行假设检验。当总的方程不显著时，表明该多元回归方程线性关系不成立；而当某一个自变量对因变量的影响不显著时，应该剔除该变量，重新建立不包含该因子的多元回归方程，筛选出有显著影响的因子作为自变量，并建立“最优”回归方程。多元回归模型的数学形式见公式1：

式中，y为因变量，影响因变量的k个自变量分别为 xk，β0，β1，β2…βk，为回归参数。

3.2 回归模型的建立

本文中对保定市2018年每天的环境空气质量指数(AQI)和二氧化硫(SO2)、二氧化氮(NO2)、可吸入颗粒物(PM10)、一氧化碳(CO)、臭氧(O3)、细颗粒 物(PM2.5)六项指标浓度数据进行多元逐步回归分析，结果见表5，表6，表7。从表5中可以看出，三个模型的R方值即判定系数依次为0.867，0.960，0.984。其中，模型3是最好的。Anova表格，见表6，是对回归分析过程所做的方差分析。模型中F值均大于3.84，说明回归方程具有很好的影响力，能够很好的表达AQI指数。三个模型整体的sig.值均为0，表明在对回归分析进行方差分析时，当自变量的取值发生变化时，其对因变量的取值都有很大的影响。从表7的系数表格可以得出，回归模型见公式2：

式中，x1为 PM2.5，x2为 o3，x3为 NO2。模型中这组数量对应的sig.值依次为0.049,0.000,0.000,0.020，都小于0.05，说明4个变量对因变量均有很好的影响力。

表5 模型汇总

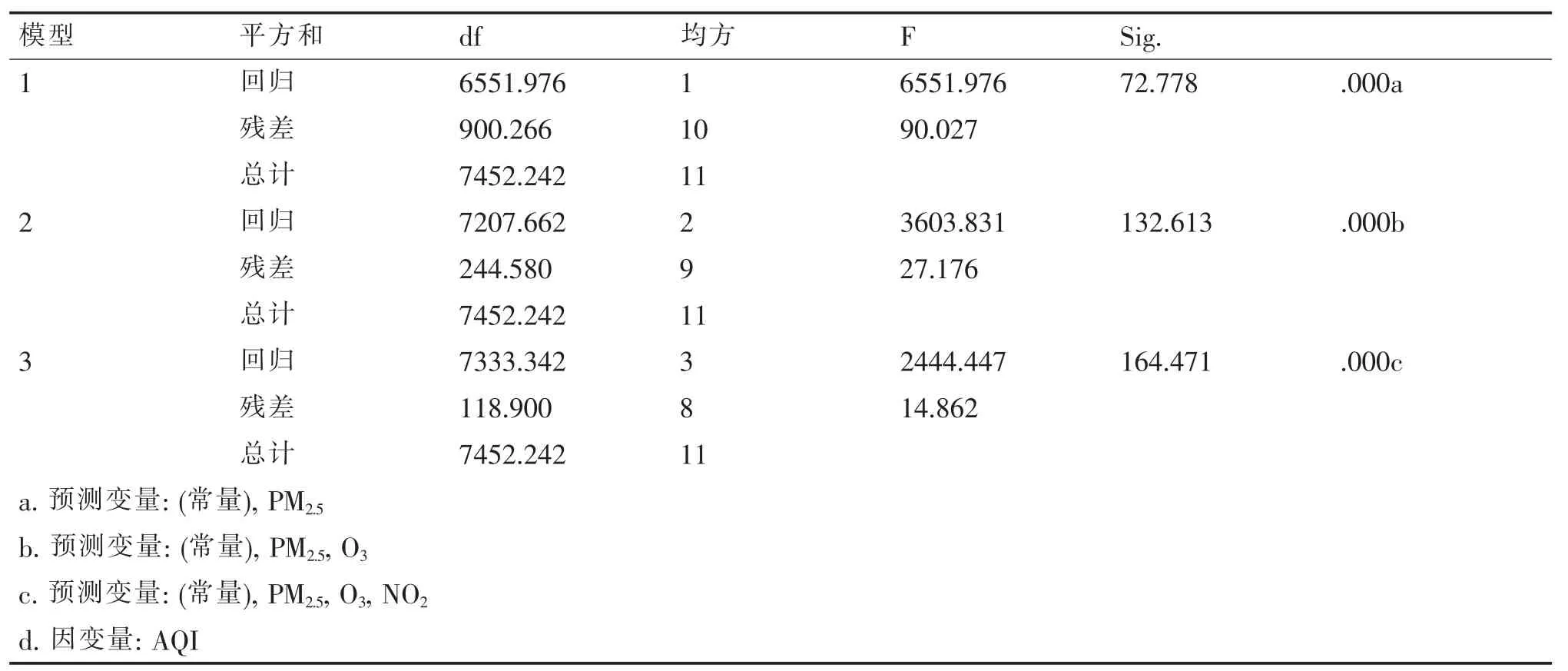
表6 Anovad

表7 系数a

4 结果分析

对保定市2018年空气污染质量浓度数据进行整理分析，发现保定市空气污染问题比较严重。文中采用因子分析法，确定了各污染源对污染的贡献率，找出了最主要的污染物为PM2.5，NO2，CO。在此基础上利用数理统计分析工具，进行多元逐步回归分析，建立了回归模型，模型效果较好。