拉脱法检测预应力的咬合力理论及其模型试验

方中明，谢发祥，张峰，张川龙，陈幼亮

(1. 南京市交通工程质量监督站,南京 210024； 2. 河海大学土木与交通学院，南京 210098；3. 山东大学岩土与结构工程中心,济南 250100)

目前为止我国已有85.1万座不同形式的桥梁，其中有数万座已成为危桥。在这些病害桥梁中，预应力混凝土桥梁所占比例约为90%。不仅我国的桥梁存在众多的安全隐患，全世界的预应力桥梁都存在类似问题。Bažant等[1-2]对全世界范围内的大跨径预应力桥梁进行了统计，结果发现日本、美国、捷克、挪威等国家的预应力混凝土桥梁均出现梁体下挠病害。Robertson[3]也指出了夏威夷一座高架桥梁的预应力箱梁出现的下挠病害。Takacs[4]研究了3座混凝土桥梁的梁体预应力不足导致出现下挠病害的案例,指出预应力不足会导致梁体开裂、下挠等病害，对桥梁结构的安全耐久性会产生极其不利的影响。因此，在实际桥梁工程中进行有效预应力检测具有显著的工程应用价值。

预应力检测技术主要分为局部有损检测和无损检测两大类。局部有损检测法主要包括预应力筋直接检测技术和应力释放法[5]。该类方法在实际结构上钻孔、切割取样，会对混凝土和钢绞线造成永久性的损伤，因此并不常用。无损检测方法主要有超声波检测法和拉脱法。研究表明张拉力与超声波的波速变化并不敏感[6-7]，超声检测法在工程中应用的精度不高。拉脱法作为一种无损检测技术[8-10]，可以比较准确地测试钢绞线锚下有效预应力，为很多实际工程中所采用。日本及中国香港的混凝土锚固规程[11-12]均规定使用拉脱法对预应力锚索的工作荷载进行检测。

国内外学者对拉脱法进行了大量试验研究和分析工作。Bruce等[13]采用拉脱法测试了大坝加固挡土墙的单孔多锚有效张拉力，认为多次的反拉测试不会对锚固系统产生实际的损害。成剑波等[8]分析了拉脱法工作原理，进行了拉脱法检测有效预应力的模型试验研究，通过张拉力-伸长量拐点确定预应力工作应力。时南翔[14]采用拉脱法进行石边坡锚索系统检查，认为检测得到的位移-荷载曲线的突变点即为预应力锚索的工作荷载。詹桂超等[10]使用拉脱法检测时，通过拉力位移曲线斜率为零的点确定有效预应力。任传亭等[6]对锚索中有效预应力不均匀的原因及影响进行了分析。李卫刚等[15]等对比分析了应变片与拉脱法测试结果，两者差异很小，表明了拉脱法的有效性。张峰等[16-19]分析了拉脱法下降段的机理，提出了咬合力的概率分布模型，给出了实际工作应力的判别准则，并进一步提出了拉脱法的时间温度修正计算方法。

在拉脱法检测有效预应力时发现，张拉力、位移或张拉力时程曲线斜率在张拉力达到最高点时发生突变，即张拉力忽然减小，随后又趋稳定[16,20]。如何对突变段进行理论分析，由反拉力确定有效锚下预应力，是亟待解决的工程实践问题。

笔者首先提出了一种获得预应力钢绞线夹片与锚板之间咬合力的理论计算方法，通过假设钢绞线变形形状，推导了夹片与锚孔之间咬合力的理论方程；然后考虑了不同的摩擦系数对咬合力的影响，计算了不同张拉力条件下咬合力的变化规律；接着进行了室内外夹片咬合力的测试，并将理论计算获得的咬合力与理论值进行了对比分析，结果吻合良好。本研究为钢绞线与夹片的间的咬合力计算提供了理论依据，为获得更准确的锚下有效预应力提供了理论支持。

图1 拉脱法曲线特征点[18,20]Fig. 1 Characteristic points of lift-off curves

1 拉脱法的典型曲线

通过大量工程测试发现[10,16,17,20]，采用拉脱法检测桥梁钢绞线有效预应力时，在钢绞线延伸量到达一定数值时，钢绞线张拉力会发生突然下降(图1 AB段)，典型锚外张拉力测试曲线如图1实线所示，而实际的锚下应力变化时程如图1的黑色点线所示。与A点对应的C点为实际的锚下应力。目前很多工程实践中，通常采用锚外张拉力B点作为钢绞线的有效锚下拉力，是不准确且偏于不安全的。张峰等[18]、夏静等[20]对咬合力进行了实测和分析，指出了拉脱时刻的锚外、锚下力的变化规律：拉力出现突变段的原因是由于在夹片拉脱瞬间，体系受力出现了的变化，钢绞线锚外与锚下张拉力不平衡，导致预应力钢绞线出现“瞬间应力重分布”现象[16-17]。

本研究将锚孔内外力(A、C点之间)的差异称之为“咬合力”，如果能够通过分析获得咬合力，即可利用实际锚外拉力曲线特征点A处拉力值减去咬合力，求得C点处的锚下有效预应力值，而不是采用B点作为近似值，可以提高拉脱法检测有效预应力的准确性。

2 咬合力理论分析模型

2.1 咬合力的间接求法

为分析锚固系统中夹片与锚板的咬合作用，首先应分析夹片与锚板锚孔之间的受力。如图2所示为夹片的受力模型，pj为锚孔对夹片的挤压力，fbj为锚孔与夹片两者之间的摩擦力，fbx为夹片与钢绞线之间的摩擦力，p为钢绞线与夹片之间的挤压力。

图2 夹片和钢绞线受力平衡图Fig. 2 Stress balance diagram between clip and steel strand

由于夹片的硬度远大于钢绞线，且夹片的丝牙将切入钢绞线，导致摩擦系数较大，拉脱法测试过程中，不会出现钢绞线与夹片之间的相对滑移，因此拉脱法反张拉过程中需要克服的是夹片与锚孔之间水平摩擦力，记为Fb1，可以通过式(1)计算：

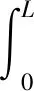
(1)

其中,pj、fbj、r1(x)分别为位置x处锚孔对夹片产生的压力、摩擦力和夹片的半径。

同时考虑到夹片的受力平衡，通过分析夹片与钢绞线水平方向的受力可得：

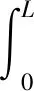
(2)

其中，fbx、r2(x) 分别为夹片与钢绞线的摩擦力和x位置处钢绞线的直径。

由夹片水平方向的平衡条件可知：

Fb1=Fb2

(3)

因此，如果获得Fb2，即在钢绞线与夹片的摩阻力，就可以求得夹片与锥孔之间的水平合力Fb1，即拉脱法检测所需要克服的夹片与锥孔之间的咬合力。这是本课题模型和试验要解决的问题。

2.2 基本假设

为简化理论模型，本研究作以下基本假设：

1) 锚杯和夹片都是刚体，其变形忽略不计；

2)钢绞线锚固后、拉脱前，夹片与锚板的锚孔完全贴合；

3)钢绞线放张前后的最大径向变形不变，且在夹片内的变形为直线；

4)拉脱法施工过程中，钢绞线与夹片之间的摩擦系数不变，且两者不会产生相对滑动。

2.3 理论模型

为获得钢绞线在夹片内的摩阻合力，笔者首先求解预应力钢绞线放张拉以后的预应力损失，然后求得反张拉过程中的夹片与钢绞线的摩阻力，最后求得夹片与锚孔之间的咬合力。

首先建立以钢绞线为核心的基本力学模型，如图3所示。

(4)

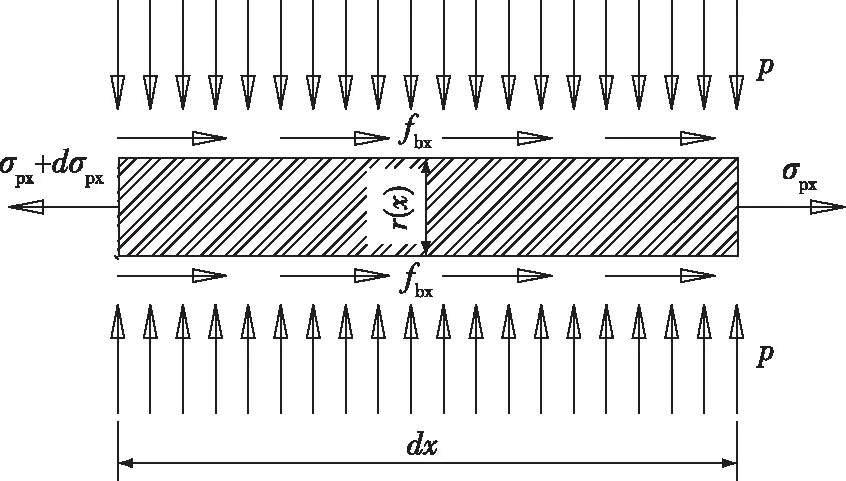
图3 钢绞线微段受力平衡图Fig. 3 Stress balance diagram of steel strand micro-section

由式(4)可以获得压力p用Δye(x)、fpx为参数的表达形式：

(5)

将式(4)代入式(5)可以得到：

dσpx(rp-Δye(x))=2μ·p·dx

(6)

整理式(6)，可得到钢绞线微段的平衡微分方程：

(7)

方程(7)是关于变量σpx的一阶变系数微分方程，可通过四阶龙格库塔方法求解，获得数值解，从而得到沿着夹片方向的钢绞线轴向应力σpx和压应力p的分布形式，即可获得钢绞线放张后导致的锚板下的预应力损失(σcon-σpe)。

获得钢绞线轴向力σpx以后，根据式(8)可以获得钢绞线轴向摩擦力：

(8)

进而可以获得放张后钢绞线咬合力合力的大小，即为夹片与锚孔之间的咬合力：

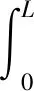
(9)

由于拉脱法检测反张拉时，锚板内外的拉力与放张后的情况不同，式(9)所得到的咬合力并不是拉脱时刻的咬合力。但是通过同样的方式可以求得由于预应力损失导致的反拉摩阻力合力的大小。图4a表示放张以后夹片长度范围以内预应力钢筋的变形情况。由于预应力损失，锚下预应力钢筋的有效预应力σpe<σcon，而拉脱法检测时，重新反张拉至控制应力σcon即可达到恰好拉脱的状态，此时钢绞线的变形形状如图4b所示。

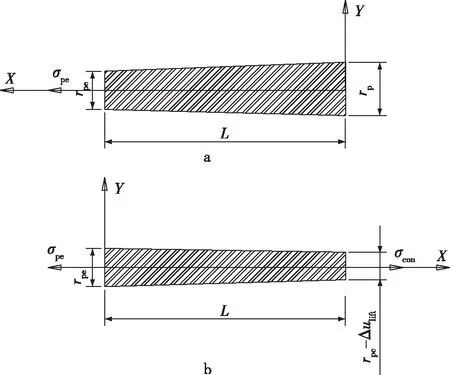
图4 钢绞线在不同拉力状态下的变形Fig. 4 Deformation of steel strands under different tensions

拉脱法检测时，锚下钢绞线应力为有效应力σpe，右侧反拉段的张拉应力为控制应力σcon，此时变形如图4b所示，在左右不等拉力作用下的变形差异Δulift为：

(10)

由假设4，钢绞线的变形形状为直线，通过类似求解方法和过程，用式(10)计算出Δulift代替式(7)的Δumax即可以获得拉脱法检测时夹片的咬合力大小。

2.4 钢绞线变形形状

为考虑钢绞线受拉的变形形状对钢绞线预应力损失的影响，由假设1，在夹片与锚具都是刚体的情况下，可假设钢绞线变形形式为直线，其沿着x方向径向的变形大小设为：

Δye(x)=ax/L=Δumax·x/L

(11)

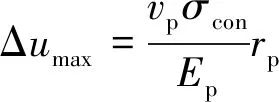
2.5 咬合力求解步骤

综上所述，夹片与锚板之间的咬合力间接求解的基本步骤如下：

1)确定基本结构参数，包括钢绞线弹性模量、泊松比、控制拉应力、钢绞线与夹片摩擦系数和钢绞线受力变形模式；

2)采用四阶龙格库塔方法求解式(7)，获得沿着锚具夹片长度方向的钢绞线轴向力，获得放张后的有效预应力大小；

3)采用式(10)求解钢绞线拉脱状态下的变形差异值，并代替式(7)的Δumax获得新的钢绞线分布形状，以及钢绞线拉脱状态下的变形形状Δy′e(x)=Δulift·x/L，再次求解式(7)，获得锚具夹片长度方向的钢绞线轴向力；

4)利用式(2)求解在拉脱状态下钢绞线与夹片水平方向的合力，其大小也就是夹片与锚孔的水平咬合力。

取钢绞线与夹片的摩擦系数为1.0，利用本研究的方法求得放张后以及拉脱瞬间，钢绞线不同张拉力下沿夹片长度方向的预应力和咬合力分布情况，如图5～8所示。

图5 不同张拉力下放张后夹片内预应力变化曲线Fig. 5 Prestressing variation curves in clips after different tensions are released

图6 不同张拉力下拉脱时夹片内预应力过渡曲线Fig. 6 Prestressing transition curves in clips under the lift-off of different tensions

图7 不同张拉力下放张后钢绞线剪应力变化曲线Fig. 7 Shear stress variation curve of steel strands after different tensions are released

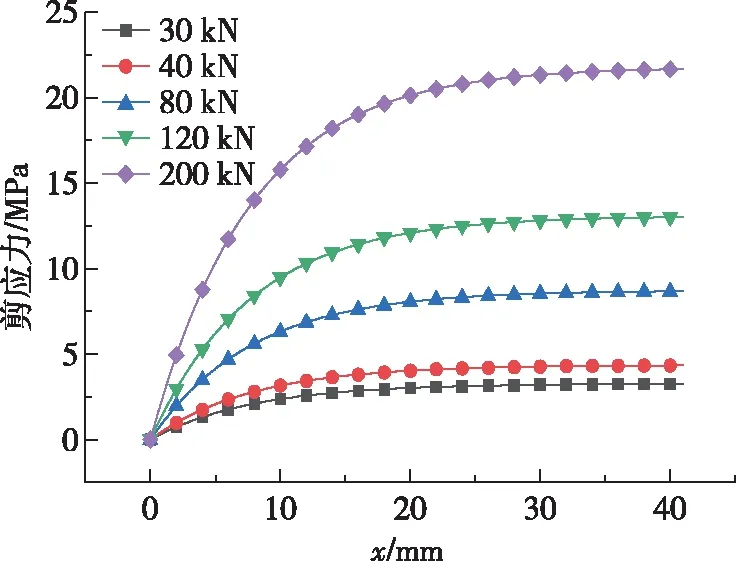
图8 不同张拉力下拉脱时钢绞线剪应力变化曲线Fig. 8 Shear stress variation curve of steel strands under the lift-off of different tensions

2.6 计算结果和讨论

由式(7)可见，除了钢绞线在拉力作用下的径向变形形状，影响微分方程的另一个参数是钢绞线与夹片的摩擦系数，为此本研究选择几种不同的摩擦系数进行计算。

本研究取直径为15.2 mm的钢绞线进行计算。模型的基本参数取值如表1。

由图5可见，不同控制张拉力作用下放张后，锚固夹片内预应力钢绞线的应力状态差异较大，从锚固端应力为零，快速变化为锚下有效应力。夹片拉脱瞬间，由于锚具内外拉力不平衡，导致夹片内钢绞线存在应力的过渡现象，其变化趋势如图6所示。

表1 模型计算参数表Table 1 Parameters of the calculating models

不同控制张拉力作用下，钢绞线与夹片之间的剪应力分布情况如图7、8所示。可见，在夹片内，剪应力的分布也是非线性的，在夹片头部为零，而在夹片尾部达到最大，这与文献[23]的有限元计算结果比较接近。

采用不同的摩擦系数(0.50～5.00等9种)计算获得的不同张拉力下夹片与锚板的咬合力曲线见图9。由图9可见，在摩擦系数一定的情况下，咬合力与张拉力呈线性关系，随着张拉力的增加，咬合力线性增加。而随着摩擦系数的增加，同一张拉力作用下，咬合力随着张拉力的增加而减小。这是由于摩擦系数增加，导致钢绞线在夹片两侧的预应力损失减小，从而导致钢绞线在夹片两端的变形差减小，使咬合力反而减小。

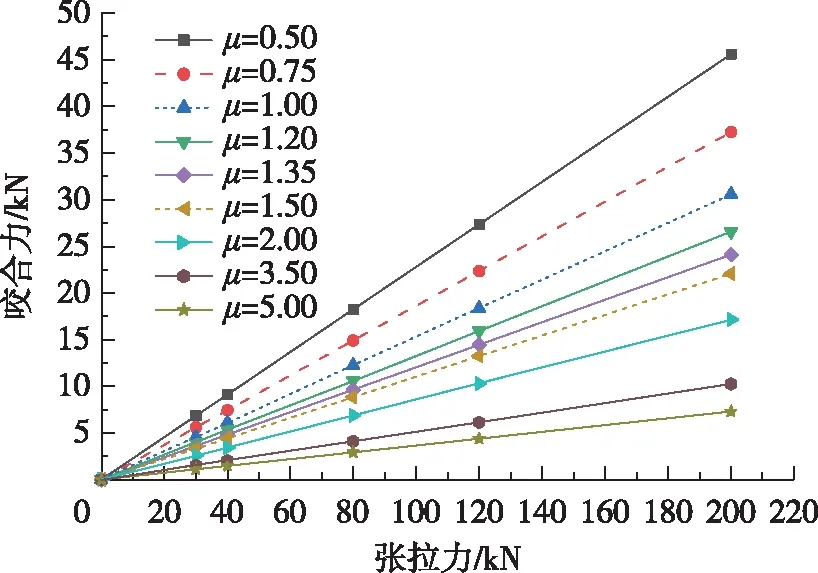
图9 张拉力与咬合力关系曲线Fig. 9 Relationship between tension forces and biting forces

3 拉脱法咬合力试验测试

3.1 室内试验

为验证理论分析结果，本课题设计了夹片咬合力的室内模型试验以及试验方案。

步骤1：在锚具锥孔狭窄段安装张拉设备并进行反向张拉，采用压力传感器控制张拉到指定吨位，使夹片和锚具咬合紧密(图10 步骤1)；

步骤2：反向缓慢使得油泵回油(图10 步骤2)；

步骤3：在锚具锥孔张开端安装正向张拉装置，张拉至夹片与锚具脱离，得到张拉力峰值，此峰值即为夹片和锚具的咬合力(图10 步骤3)。

图10 千斤顶张拉示意图Fig. 10 Schematic diagram of jack tensioning

3.2 室内咬合力测试数据分析

采用以上步骤对钢绞线不同张拉力下的咬合力进行测试，共测试326个样本，测试结果见图11。由图11可见，试验数据总体的规律性比较明显：首先，测试数据呈现张拉力越大，则测试所得咬合力也越大的基本变化规律；其次，同一张拉力下，咬合力的离散性比较大，这可能是由于不同夹片与锚板的摩擦系数不同导致的。

将测试数据与不同摩擦系数情况下的咬合力计算值绘制在图11上。由图11可见，理论值与实测值的基本趋势一致，不同摩擦系数情况的咬合力理论值能够覆盖测试值范围。

图11 室内试验咬合力与回归值对比Fig. 11 Comparison between theoretical and measured values of biting forces

3.3 现场拉脱法实测

本研究同时依托实际桥梁工程中的预应力钢绞线开展拉脱法测试研究，测试梁为20 m T梁，钢束布置参见图12。试验方案如下：

1)仅张拉20 m T梁的N1和N2波纹管道中一根钢绞线，将电阻式压力传感器置于锚下(图13a)，张拉到指定吨位，对锚下预应力进行采集，采样频率为20 Hz。

2)在锚具与油泵中间放置另一个压力传感器(图13a)，检测拉脱法有效预应力(图13b)，在夹片脱开时，观察并记录锚下与锚外压力传感器压力数值。

图12 20 m T梁横截面图Fig. 12 Cross section of 20 m T-beam

图13 现场试验示意图Fig. 13 Schematic diagram of field tests

3.4 梁体试验结果和分析

现场梁体共测试了53组数据，部分测试曲线如图14所示。由图14的梁体拉脱法实测曲线可见，在夹片拉脱瞬间，反拉力有明显下降，而锚下传感器获得的有效应力也明显低于拉脱瞬间反张拉传感器的测试值，与文献[18,20]描述吻合。

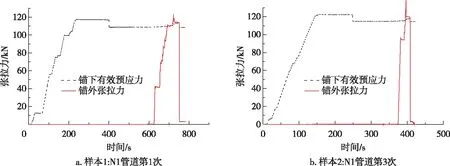
图14 部分现场检测曲线Fig. 14 Partial field detected curves

分别计算室内试验、梁体试验以及室内试验+梁体试验的拟合曲线，可以得到3个不同斜率的曲线，如图15所示，对应的斜率和摩擦系数如表3所示。由图15和表3可见，梁体咬合力测试数据以及和室内试验数据的集合仍然能够保持良好的直线关系，直线拟合的R2均在95%以上，说明本研究提出的咬合力与张拉力的直线关系是正确的。从已有的测试数据来看，可用全部咬合力数据的拟合计算不同张拉力下的咬合力，即：

ybite=0.152 5·xcon

(12)

其中，ybite、xcon分别为咬合力(kN)和实际张拉力(kN)。

利用式(12)可以求得该斜率下相应的钢绞线与夹片的摩擦系数为1.012，而钢材之间的摩擦系数一般取值为0.05～0.30[23]，但是由于夹片丝牙的咬合作用，钢绞线与夹片的摩擦系数较大。

图15 张拉力与咬合力的试验拟合Fig. 15 Test fitting of tension and biting forces

表3 不同试验数据的拟合结果Table 3 Fitting results of different test data

为了对工程实践更有指导意义，本研究同时计算了具有95%保证率的咬合力方程：

ybite_upper=0.152 6·xcon+9.007 7
ybite_lower=0.152 3·xcon-9.007 7

(13)

其中，ybite_upper、ybite_lower分别为具有95%保证率的咬合力上下限值。

式(13)与实测值的对比如图16所示。由图16可见，本研究所提的咬合力上下限值能够较好地体现咬合力变化范围。

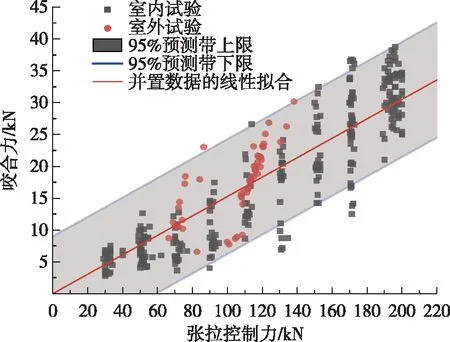
图16 咬合力上下限Fig. 16 Upper and lower limits of biting forces

4 结 论

拉脱法是一种有效的桥梁预应力检测方法。为准确评估拉脱法测试的锚下有效预应力，笔者提出了一种通过钢绞线变形分析夹片与锚孔之间咬合力的理论计算方法，分析了摩擦系数对咬合力的影响，结合室内锚具和室外梁体的咬合力试验，将理论计算值与实测值进行了对比，获得的主要结论如下：

1)拉脱法检测钢绞线有效预应力时出现拉力突变的原因主要是由于需要克服咬合力以及随之出现的瞬时内力重分布效应所致。

2)通过分析钢绞线变形特征，笔者提出的拉脱法咬合力计算方法能够准确反映咬合力变化趋势，与实测咬合力的吻合程度较高。

3)理论计算和试验结果显示，咬合力与张拉力呈线性关系变化，张拉力越大，咬合力越大。咬合力和夹片与钢绞线的摩擦系数呈负相关，相同张拉力情况下，钢绞线与夹片的摩擦系数越大，咬合力越小。

4)综合现有的室内外试验结果，可以采用室内外试验数据拟合公式ybite=0.152 5·xcon计算咬合力大小。