基于m序列泊松分布统计模型仿真实现

刘 市，王永超，杨国学

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

0 引言

随着全球卫星导航系统的快速发展，尤其是北斗全球系统的建成使用，卫星导航系统应用越来越广泛，人们对于设备的性能要求也越来越高。卫星导航信号模拟源可以为各类终端测试提供真实卫星导航系统的高精度模拟,可在受控的实验室环境中为终端设备的研制、测试、生产等环节提供可重复、可选择的测试验证支持。而入站信号统计模型仿真是入站源模拟信号生成的关键技术指标之一，要求实现一定容量入站信号的泊松分布统计模型仿真。

本文采用m序列伪随机函数作为信号播发的基础控制参数，保证了统计模型中播发信号的随机性，同时融入泊松分布的控制参数，实现入站信号统计统计模型仿真。

1 泊松分布统计模型仿真技术

1.1 m序列及泊松分布分析

m序列是由多级移位寄存器或其延迟元件通过线性反馈产生的最长码序列，具有随机性。对于周期为P的两个循环序列{an}与{an-τ}的自相关系数ρ(τ)为

(1)

在二进制序列情况下，只要比较序列{an}与移位后序列{an-τ}对应码元，即：

(2)

其中，A为对应码元相同的数目，D为对应码元不同的数目。对于m序列，其码长为P=2n-1。根据m序列特性，“0”的个数为A=2n-1-1，“1”的个数为D=2n-1。根据移位相加特性，m序列{an}与移位后序列{an-τ}进行模2加后，仍为m序列，所以“0”和“1”的码元个数仍差1。因此可得m序列的自相关系数为

(3)

可知，当周期P越大，m序列的自相关特性越好。

泊松分布是统计某件事件在某时间区间内发生的次数的模型。根据泊松过程的定义，将时间区间(0,t]分成n等份，使得每等份的长度为h=t/n足够小。由泊松定义可知

P{N(h)=1}=λh+o(h),P{N(h)=0}=1-λh-o(h)

(4)

其中λ为单位时间内事件平均发生的次数。在每个小时间区间h上，事件是否发生是一个近似Bernoulli的随机变量，记为X[m]，m=1,…,n，因此，独立同分布Bernoulli序列X[m]的和过程N[nh]就是一个二项式计数过程

N[nh]=X[1]+…+X[n]

(5)

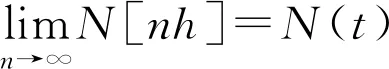
根据二项计数过程的一维概率质量函数式可知

(6)

由此得泊松过程的一阶概率质量函数为

(7)

1.2 基于m序列的泊松分布统计模型

入站模拟源信号特性：

入站模拟源于每秒的秒初作为起始时刻发射模拟信号；

入站模拟源可同时播发20个通道的射频信号;

入站模拟信号长度可变，根据入站模拟信号长度及时延，可将发射频度分为1s/次和2s/次两种。

采用m序列构建泊松分布模型，以单个序列状态表示通道发射信号状态，构建表示式如下所示：

(8)

i时刻m序列值ai*20+j=1时，j通道发射入站信号，即Xi*20+j=1。

由于m序列“1”的个数比“0”的个数多一个，即当P值较大时，可认为“1”的个数占m序列总长度的1/2。为满足单位时间内期望信号发射概率λ/(n*20)，需将m序列“1”的“长度”进行伸缩，设m序列单个序列状态标准时间为Tm，需伸缩“长度”为y，则

(9)

得出

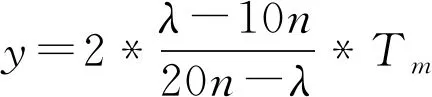
(10)

即m序列“1”的“长度”变为Tm+y。工程实现中，m序列“1”的“长度”不变，为Tm，设Tk为从信号播发开始计算的y的叠加次数，当Tk=k*y>Tm时，增加一次信号播发，当Tk=k*y<-Tm时，减少一次信号播发。计20通道信号播发使能为Ei(i=1,2…20)，20个通道的信号播发时能设置完成后，当下一秒脉冲到来时，实现20个通道的信号播发，20个通道的信号播发使能设置重新开始计算。如图1所示。

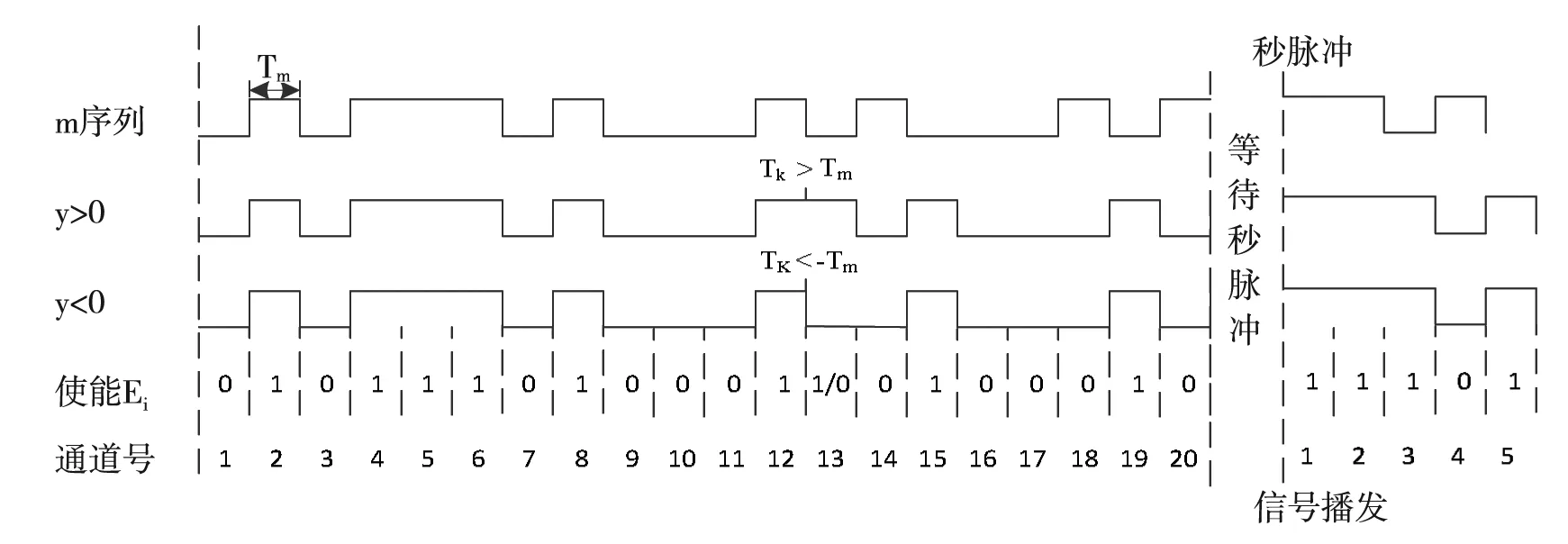
图1 m序列控制信号播发实现框图

由于入站模拟信号播发频度分为1s/次和2s/次两种，需增加信号播发条件。假设通过电文长度和通道时延计算，通道i为2s/次的播发频度，则在m序列控制信号播发实现时，若通道i在上一秒信号播发使能，则当前秒通道i不进行信号播发，而信号播发使能状态顺延到下一通道。假设通道8播发频度为2s/次，且上一秒播发使能，则当前秒对其轮空判断，信号保持上一次使能状态，示意图如图2所示。

图2 信号播发控制实现框图

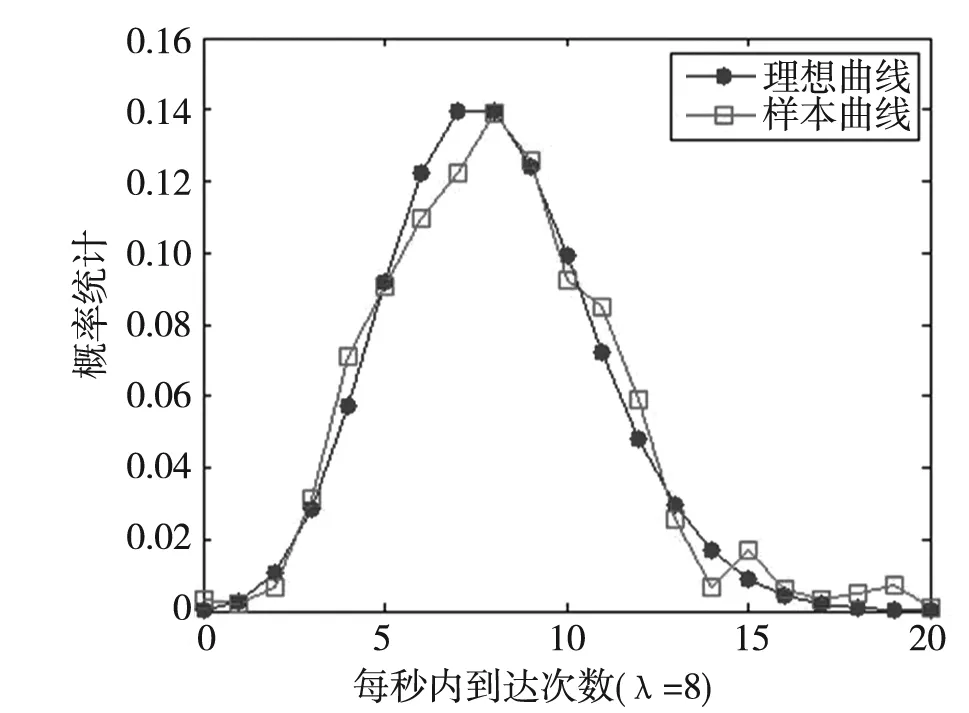
图3 泊松分布模型matlab仿真

在本设计中，采用24级m序列实现，多项式G(x)=x24+x6+x4+x3+1，初相根据当前系统时间计算得出，充分保证了信号播发的随机性。

1.3 仿真实现

设置λ=8，n=1,即单位时间内最大20，共仿真1000次，得到matlab仿真图如图3所示。

由泊松分布模型matlab仿真可知，基于m序列的泊松分布统计模型与泊松分布理想曲线基本一致。

2 结束语

基于m序列的泊松分布统计模型仿真实现，保证了模型仿真中信号播发的随机性，同时根据系统时间设置m序列初相值，实现了信号播发过程的不唯一性。