基于Kriging模型优化算法的含分布式电源配电网多目标无功优化研究

石佩玉，田晓军，路文梅，李 燕，高 波，李彤坤

(1.河北水利电力学院 电气工程学院，河北 沧州 061001；2.沧州市工业机械手控制与可靠性技术创新中心，河北 沧州 061001；3.河北工业大学，天津 300130)

分布式能源包括风能、太阳能光伏、储能系统等。大规模分布式电源并网势必改变配电网的潮流分布，使电网中的无功潮流改变，若某个节点无功不足或过剩，则会降低电压质量[1]。在实际运行中，由于分布式电源 DG和大部分负荷都具有较强的随机性，通过直驱式风电机组和光伏系统逆变器可以对并网功率实现有功功率和无功功率独立调节。因此，研究考虑源荷不确定性的含DG配电网的多目标无功优化策略十分重要。

1 含DG配电网多目标无功优化模型

1.1 源荷不确定性的描述

风力发电机的有功输出和风速有关，风速一般服从威布尔分布[2]，威布尔分布的形状、尺度参数由风速24h观测均值和方差计算得出，则风电发电机组有功功率输出与额定风功率出力及额定、切入和切出风速有关。太阳光照强度beta分布模拟[2]， beta分布的形状参数由光照的平均值和方差计算，有功功率输出与方阵面积和转换效率等有关。负荷功率概率分布采用正态分布进行模拟。本文考虑的储能装置(ESS)为电化学储能，设其在控制周期内的充放电过程以恒功率进行。

由于分布式电源和负荷均具有随机性，储能装置作为可控负荷和电源，对削谷填峰改善电压有积极作用。对于随机性源荷，本文采用拉丁超立方采样，具体方法为：对每个随机变量的累积概率分布曲线的纵轴等概率分成N个空间，有P个随机变量，则通过采样后得到一个N×P的采样矩阵，通过迭代计算，最后形成N个采样场景，场景集合为SC。为满足抽样规模，N取值大，精度高，但降低了计算效率，因此可采用同步回代削减SBR技术[3]进行场景削减，通过计算场景间的概率距离，找到与其距离最短的场景，合并相似的场景并确定相应概率。

1.2 目标函数

基于源荷不确定性，选取分布式电源、无功补偿装置和储能放电时的无功出力为连续控制变量，电容器组无功投切容量、有载调压器(OLTC)分接头位置为离散控制变量；以DG投资效益B最高、网络有功损耗Ploss最小及节点电压偏差dV最小建立多目标无功优化模型。即：

(1)

对目标进行归一化处理，

(2)

采用权重系数法，建立满意度函数：

f=aα1+bα2+c(1-α3)

(3)

以有功损耗为主的层次分析法确定a、b、c分别取值为：0.1，0.7，0.2。

1.3 约束条件

2 基于Kriging模型全局优化算法的无功优化求解策略

2.1 多阶段求解方法

约束条件中考虑离散变量投切次数，并考虑了求解时段的划分，使所建立模型不易直接求解。因此根据被控量的调节特点将其划分为基础调节量和补充调节量。求解过程分三个阶段：

第一阶段，以电容器组数、有载调压器(OLTC)分接头位置、DG、SVC及放电状态下ESS的无功出力为控制变量，不考虑前二者的动作次数限制，以每个小时满意度为目标，计算24h内每小时每个控制量取值。

第二阶段，只考虑电容器组数和OLTC分接头位置作为基础调节量，连续变量保持不变，以24h满意度为目标函数，同时考虑离散变量动作次数约束和节点电压约束，计算得出每个小时的电容组投切容量和OLTC位置。

第三阶段，DG、SVC、ESS无功出力作为补充调节量再调整，离散变量保持不变，以每个小时的满意度为目标，固定第二步离散变量值，计算得出每小时DG、SVC无功出力，并根据ESS状态确定其无功出力。

通过三个阶段，得到以满意度最接近于1为目标的每小时内控制变量的值。

2.2 基于Kriging模型全局优化算法求解含DG配电网多目标无功优化

多阶段求解方法中，每一阶段都是对某个配电网无功优化模型的求解。本文提出基于Kriging元模型的全局优化算法并用于求解配电网多目标无功优化问题。

(4)

初始设计区域、目标函数和约束条件、设计变量为已知，在初始设计区域中进行采样，应用目标函数及约束条件对试验点进行评估，将实验区域进行分割，在分割后的区域中再进行采样和Kriging模型拟合，局部优化。基于Kriging元模型全局优化算法求解无功优化问题的流程如图1所示。

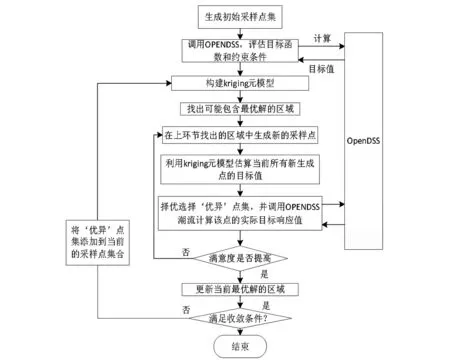
图1 基于Kriging元模型全局优化算法的无功优化求解流程

3 算例介绍及仿真分析

无功优化方法的数值模拟和仿真计算由MATLAB完成，潮流计算由OPENDSS完成，基于Kriging元模型的全局优化算法在MATLAB上实现，并调用OPENDSS来进行目标函数和约束条件计算。以改造后的IEEE33节点配电系统为例。如图2所示，参数如下：保持线路参数不变，OLTC电压比范围为0.9～1.1pu，上下共16挡位，步进量为0.625%；ESS为储能装置，放电功率上限为0.24MW，荷电状态为30%～90%，充电效率为80%，放电时具有无功调节能力。DG1、DG2为直驱式风电机组，DG3为光伏系统，SVC1和SVC2的补偿容量取-600kvar～600kvar；C1和C2为两台并联补偿电容器，每台7组，每组补偿容量为100kvar；OLTC、电容器的日最大调节次数均设置7次，单次动作成本为6元[5]。各节点电压取值范围0.95～1.05pu；系统三相功率基准值SB=10MVA，线电压基准值为UB=12.66kV；结合场景削减算法，在24h内得出10个削减后的场景，分别为sc1,sc2…sc10，并得出每个场景的概率，psc1，psc2…psc10。如表1所示。本文列出t=14h风电出力场景、光伏出力场景、负荷场景情况，如表2-表4所示。

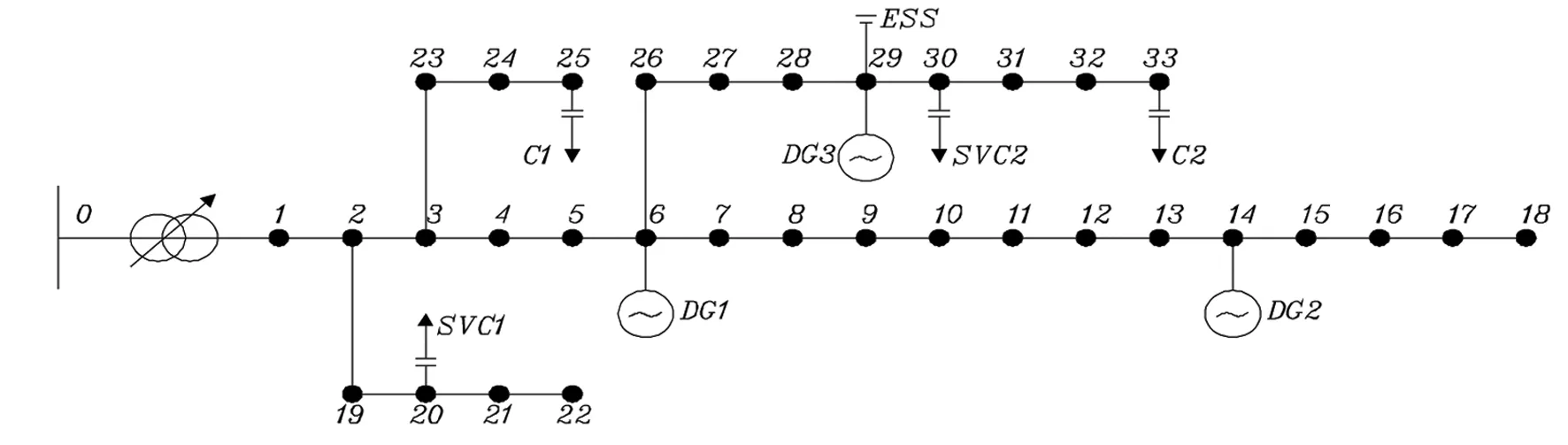
图2 改造后的IEEE33节点测试系统

表1 削减后各场景概率

表2 t=14h风力出力场景

表3 t=14h光伏出力场景

表4 t=14h负荷场景

以t=14h为例，对是否考虑源荷不确定性及动作次数约束的无功优化结果进行分析，校验结果如表5。

考虑源荷不确定性和动作次数限制的无功模型与既不考虑源荷不确定性又不考虑动作次数限制的无功模型都有较高的满意度，但考虑源荷不确定性和动作次数限制的无功模型更符合实际运行的情况，具有更好的适应性。

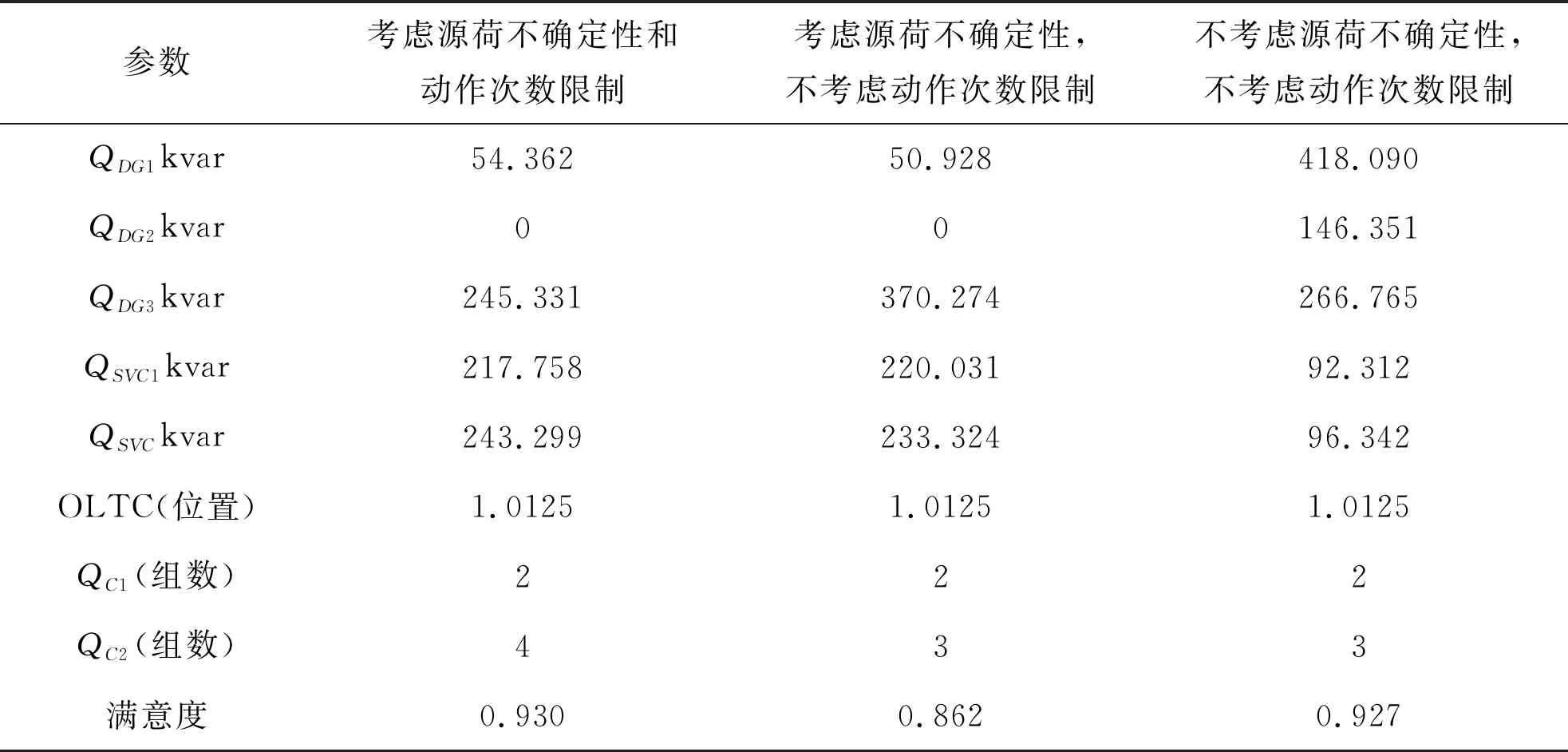
表5 t=14h各情况的最优无功计划

为测试本文提出的基于Kriging元模型全局优化算法的有效性，将其与已有文献中的粒子群算法(PSO)对比。粒子群算法初始参数为：初始种群设为20，最大、最小惯性权重分别为0.9,0.6，学习因子均取2.0[6]。两种算法无功优化结果如表6，以t=5h为例。

表6 t=5h优化结果及算法性能对比

通过对比分析，应用本文提出的基于Kriging模型的全局优化算法在满意度、平均评价次数及平均计算时间上都优于粒子群算法，有效提高了寻优速度和求解效率，并有较好的全局收敛性。结合本文构建的无功功率优化模型，更好地解决了分布式新能源环境下配电网多目标无功功率优化问题。