一种新的基于PRM的多端口微波器件测量方法

宋 蒙，李光福

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081;2.中国电子科技集团公司第十三研究所，河北 石家庄 050081)

0 引言

利用传统的两端口的矢量网络分析仪(VNA)来测量与校正微波器件的散射矩阵的方法已经趋于成熟。然而，对于n端口的散射矩阵网络测量一般需要用以下两种方法。第一种方法是利用n端口的矢量网络分析仪直接测量，第二种方法是利用端口还原法(Port Reduction Method)。

在第一个方法中,可能需要一个特殊的多端口的矢量网络分析仪[1]，并且需要相应的特殊校准工具箱[2],从而能够校正掉每个端口之间能量耦合的影响。Sharma和Gupta提出利用n端口矢量网络分析仪校正n端口微波网络矩阵误差的方法[3-4]。然而，目前多端口网络分析仪造价昂贵，一般采用的较少。第二种方法是利用传统的两端口矢量网络分析仪来测量，通过n端口的微波器件连接理想的终端负载来较少需要测量的端口。特别是在高频需要探针台测量的时候，这种方法应用非常广泛。Lin和Ruan提出的PRM算法中，多端口微波器件是在一系列端口多次连接[5]。后来Tah-Hsiung Chu提出在多端口微波器件可以一次连接多个终端负载[6]，但是该算法中需要三种终端负载类型，本论文提出的基于PRM的新型算法只需要两种终端负载，简化了测量子电路的设计和数量。

1 PRM算法的基本理论

PRM算法是指利用多组n-1端口的散射矩阵来组合计算出n端口的散射矩阵网络。传统的PRM算法的基本流程如图1所示。

图1 传统的PRM算法测量多端口微波网络流程图[7]

在PRM算法中，选择四端口定向耦合器的两个端口作为实际的测量端口，连接矢量网络分析仪。其余两个端口需要连接短路，开路以及3dB衰减器端口三种端口负载才可以计算出n端口的微波网络。但是在实际的测量中，3dB衰减器由于带宽和衰减平坦度的问题，不但给测量增加了额外的误差，而且增加了测量的成本，本文提出的PRM算法仅需要短路和开路两种端口终端负载就可以重新组建出n端口的散射矩阵。

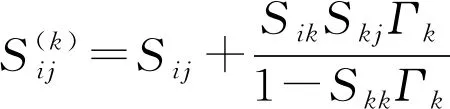
(1)

如果在n端口的微波网络中的第n个端口连接两种不同的终端负载，在第n-1的端口连接一个终端负载。这样可以得到三组n-1端口的散射矩阵，通过这三组n-1端口的散射矩阵可以还原得到n端口的微波网络的散射矩阵。

假设其它的端口连接在n-1的端口上，这个终端负载的反射系数记为Γn-1，而在第n个端口上连接两个不同的终端负载，这两个终端负载的反射系数记为Γn1和Γn2。可以得到：

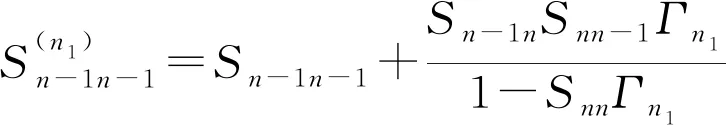
(2)

(3)

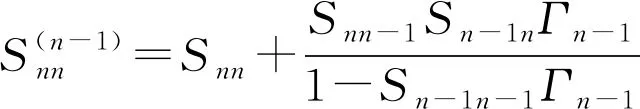
(4)

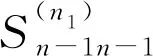
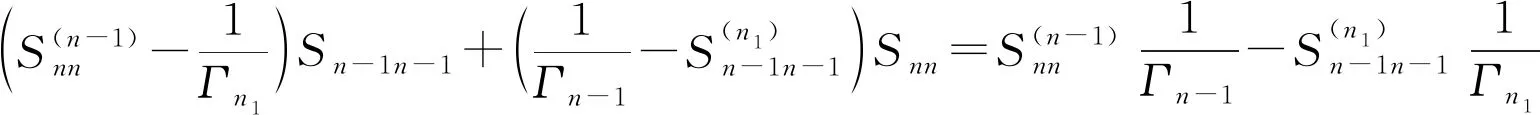
(5)

(6)

联立方程(5)和(6)就可以解出n端口散射矩阵的Snn，Sn-1 n-1，对于i和j小于或等于n-1的Sij能够根据公式(7)解出来：

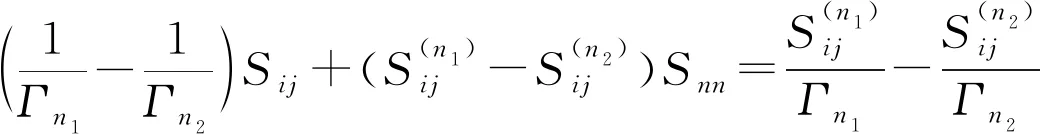
(7)

将计算出来的Sij和Snn带入公式(8)可以得到SinSnj：

(8)

假设

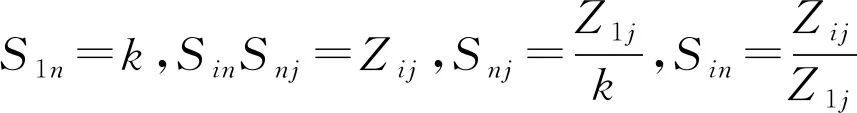
(9)

根据公式(4)可以得到：

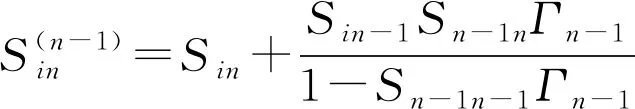
(10)

当i=1时，

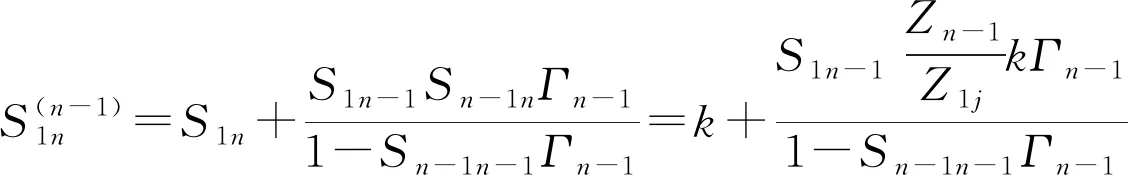
(11)

根据公式(11)可以解出k值。因为Snj=Z1j/k，这样就解出了Sin，Snj。通过以上的分析和公式，n端口的散射参数就可以全部都计算出来。

图2 基于CCS CL的多端口定向耦合器模型结构示意图

2 测量器件建模和算法流程图

利用THz的频段的四端口的定向耦合器为例，来验证本算法的准确性。定向耦合器采用互补型传导耦合线(CCS CL)来设计[7-8]。这种互补型传导耦合线具有近横向电磁模(Quasi-TEM)的波导特性并具有二维方向布局缩小尺寸的能力。对于高性能的微波无源电路设计，互补型传导耦合线相较于传统的耦合线结构具有更宽的特性阻抗范围。另外互补型传导耦合线比传统的普通弯折的耦合线具有更多的设计结构参数，使设计耦合线更加灵活和方便。THz频段的四端口的定向耦合器的模型如图2所示，该模型基于标准的130nm 1P8M CMOS技术。参考地平面为M1-M6通过过孔堆叠相连，信号线通过M7实现。

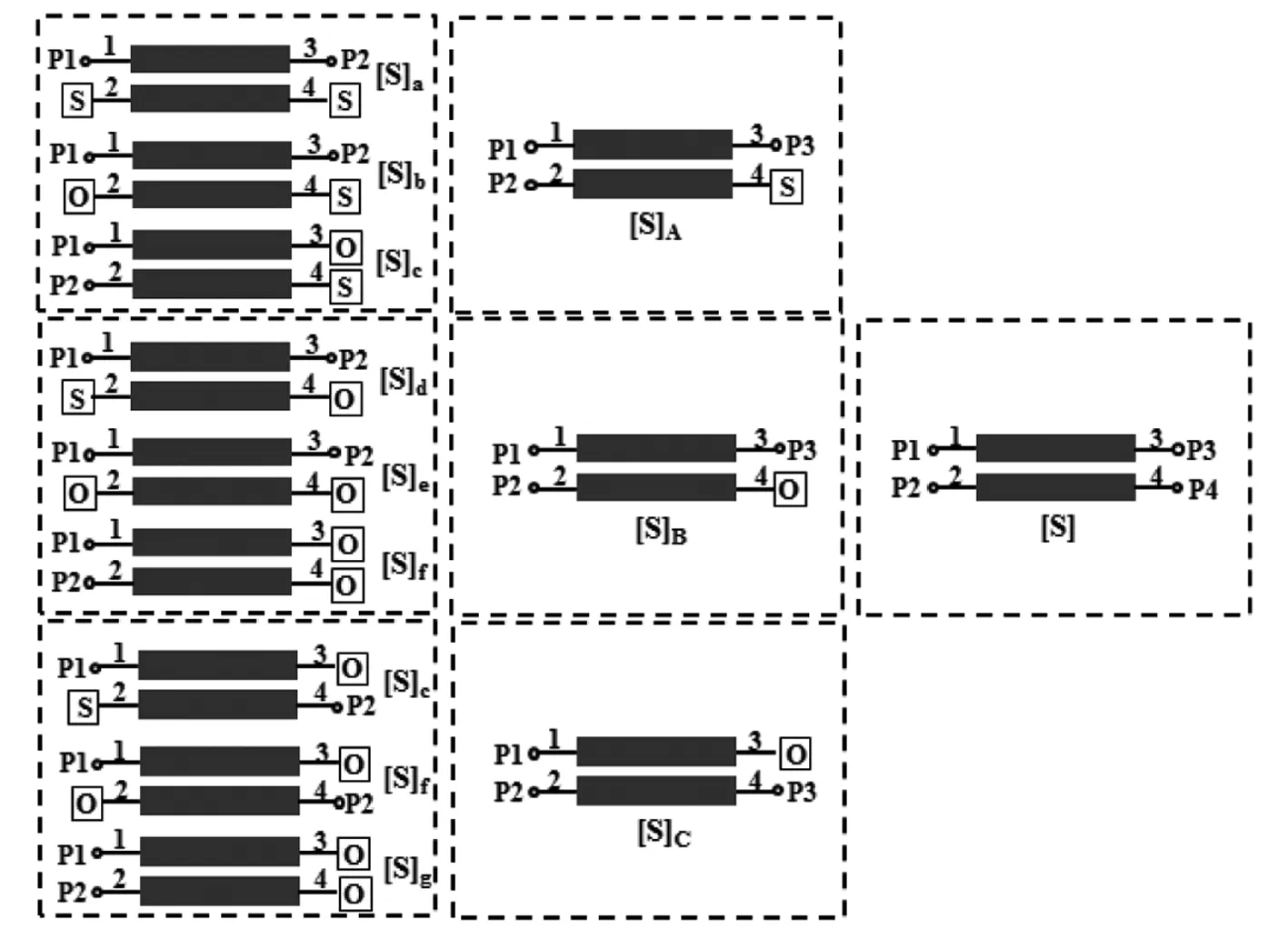
图3 基于PRM的新型测量多端口微波网络的流程图

图3是基于PRM的新型测量多端口微波网络的流程图。P1，P2表示连接矢量网络分析仪的的测量端口。S和O分别代表端口连接端口和开路的终端负载。本文提出的基于PRM的新型多端口微波网络的流程图，微波器件的端口只有短路和开路两种终端负载，与传统的PRM的测量方法相比，少了一种终端负载，简化了测量子电路的设计。这种算法是在四端口微波器件的两端连接相应的终端负载，利用三组两端口的S参数可以重组出三端口的S参数，在利用三组重组的三端口的S参数就可以组建出原始的四端口微波网络的S参数。

3 理论算法和数值分析

通过三种方法得到多端口微波网络的S参数，从而验证本算法的正确性。第一种是采用Ansoft HFSS 14.0 软件全波模拟THz频段的四端口的定向耦合器的模型得到S参数，在图中用“HFSS_全波”来标记。第二种是将全波模拟THz频段的四端口的定向耦合器的S参数导入Ansoft Designer 6.0 软件，在Designer 6.0 软件通过加入理想的开路和短路终端负载得到两端口的S参数，利用本论文提出的新型的PRM算法计算出四端口微波网络S参数，在图中用“Designer_PRM”来标记。第三种方法是采用Ansoft HFSS 14.0 软件全波模拟端口连接相应的终端负载的两端口的定向耦合器的S参数，利用本文提出的新型的PRM算法计算出四端口微波网络S参数，在图中用“HFSS_PRM”来标记。

图4和图5分别为三种算法的多端口微波网络的S参数的大小和相位。图中分别用实心的方块、圆圈和上三角符号来表示HFSS_全波、Designer_PRM和HFSS_PRM三种算法。

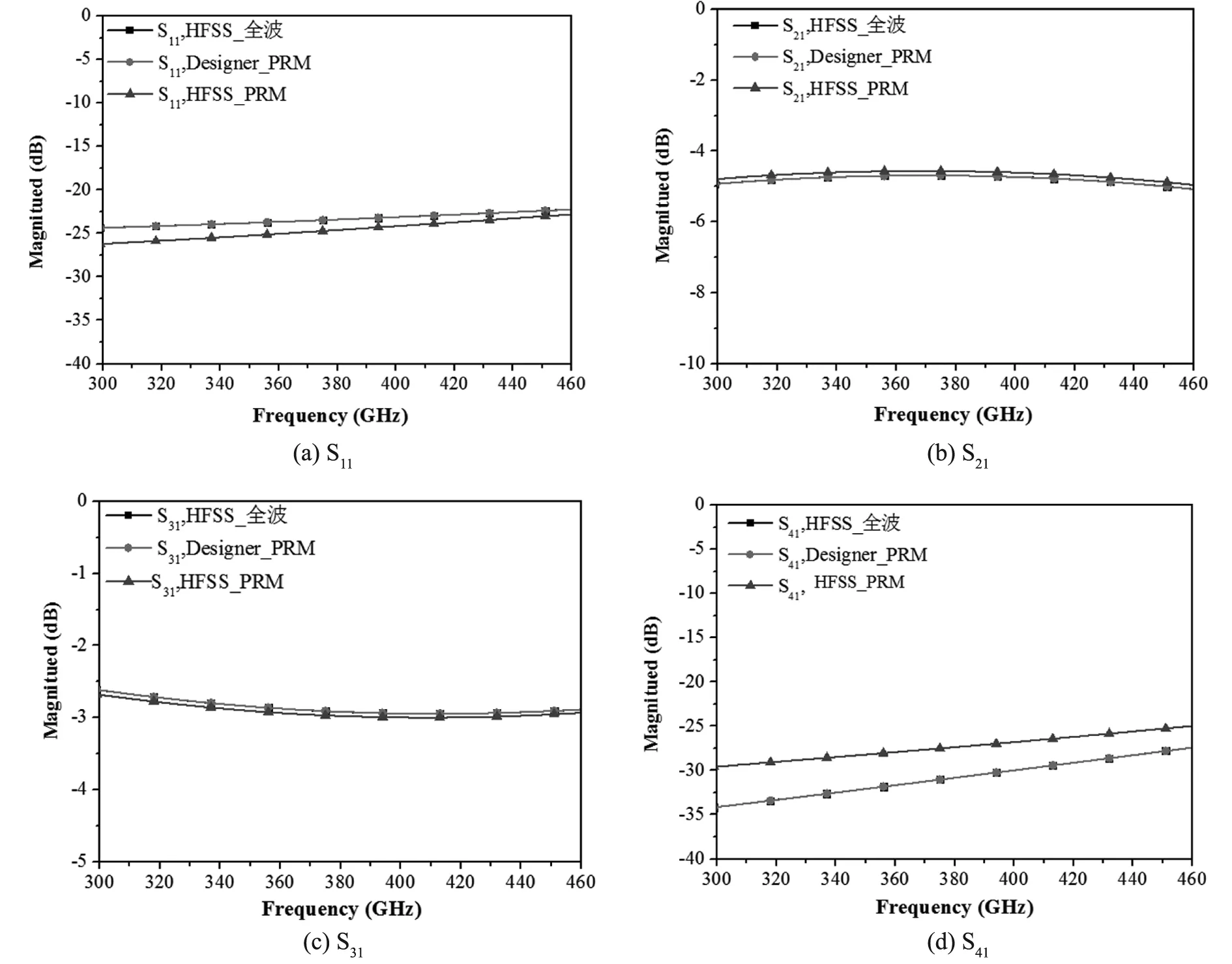
图4 三种方法得到的S参数大小对比

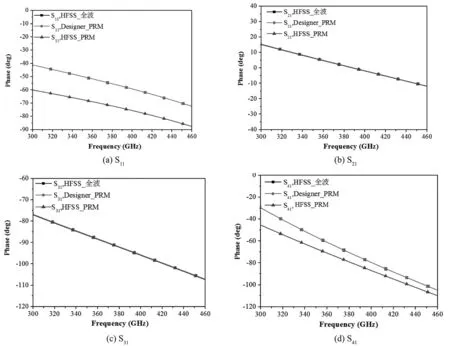
图5 三种方法得到的S参数相位对比

在图4和图5中，第一种方法HFSS_全波和第二种方法Designer_PRM的曲线是完全重合的，由此可验证本文提出的基于PRM的新型算法是正确的。而第三种方法HFSS_PRM的S参数，是在端口负载根据实际结构全波仿真得到的，端口终端负载不是理想的开路和短路，因此相应的反射系数也不是1和-1，但是如图4和图5所示，HFSS_PRM的S参数与HFSS_全波的S参数很接近，因此在实际测试中，可以用此算法来测量多端口网络的S参数。

4 结论

提出了一种基于PRM的新型多端口微波网络测量的方法，与传统的PRM算法相比，该方法只需要两种终端负载，简化了测量子电路的设计。另外通过基于互补型传导耦合线的定向耦合器建模，利用三种方法得到多端口微波网络的S参数，在Ansoft Designer中利用理想的开路短路终端负载基于提出的新型PRM算法计算出的S参数与全波模拟的S参数一样。在Ansoft HFSS中利用实际的开路短路终端负载建模，基于新型PRM算法计算出的S参数与全波模拟的S参数很接近。从而验证了本算法的可行性和正确性。