多退化失效模式下基于功能仿真的可靠性建模方法研究
贾占强,杨建永
(中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
利用产品的退化数据来实现高可靠、长寿命产品的可靠性评估越来越受到重视,随着研究的不断深入,人们取得了大量研究成果[1-5],多退化失效模式下可靠性评估方法不断突破。刘洁梁等[6]从产品的多个失效模式出发,考虑退化量之间的相关性,采用线性回归方法和GM(1,1)模型建立多退化量产品可靠性评估模型,给出了贫数据多退化量下产品的可靠性评估方法。刘晓娟等[7]提出了考虑多退化失效和突发失效之间竞争失效的可靠性评估方法。综合来看,上述研究方法是将研究对象作为一个整体对待,通过对系统退化参量进行分析进而实现产品的可靠性评估。而实际工程中,对于电子产品来讲,为了保持电路的稳定性,在电路设计时会增加滤波、反馈等稳定电路,系统长时间运行时,其性能参数虽然稳定,但其某些关键单元可能已经接近失效的边缘,面对这些实际问题时,现有评估方法可能会造成评估预计结果不准确,严重时会造成人员或装备的重大损失。
电子设计自动化(EDA)技术的不断发展为电路设计、功能性能仿真等提供了全新的手段,使用EDA技术,利用统计分析、温度(环境)分析功能,可分析电路稳定性并识别薄弱环节,对电子产品研发和功能性能验证起到了积极作用。
为此,本文针对多退化失效下的电子产品可靠性评估问题,引入系统功能仿真的方法对现有可靠性建模方法进行改进,通过EDA系统功能仿真识别关键组件或单元并确定其权重因子,利用退化失效分析理论可建立关键组件的退化失效模型,综合关键组件的权重因子和退化失效模型利用混合分布函数即可建立系统可靠性模型,进而实现电子系统的可靠性评估。
1 系统功能仿真
在传统可靠性理论中,故障模式、影响及危害度分析(FMECA)技术是一种确定系统关键重要组件的有效方法,该方法通过逐级(“元器件-功能电路-单元-系统”)开展FMECA分析,危害度为Ⅰ级的元器件或单元定义为关键单元,这种方法的优势是系统分析清晰、故障影响关系明确,对于产品研制具有积极意义;缺点是故障影响关系复杂、工作量巨大。
文献[8]提出了使用灵敏度仿真分析法确定关键组成单元的方法,灵敏度高者为关键组成单元,该方法优势是无需了解电路具体功能,只需在EDA仿真软件中配置好电原理图即可输出相关结果。受当时EDA软件功能性能及计算机硬件配置等因素限制,灵敏度仿真分析法仅适用于小信号电路模型。近年来,随着EDA仿真能力及计算机硬件的快速发展,仿真软件的能力得到了大幅提升,本文充分利用仿真工具的这一优势,将其用于识别和确定电子产品的关键组成单元,并完成灵敏度的仿真计算。
2 关键功能单元的退化失效分析
产品关键功能单元的退化失效是内部因素与外部环境综合作用的结果,其退化失效模型的确定可通过可靠性试验的统计结果来实现,其具体步骤如下:
Step 1从产品总体中随机抽取m个样品进行退化试验,可选择的试验方法有恒加退化试验、步阶加速退化试验等。
Step 2收集试验样本在时间t1,t2,…,tn的性能退化数据,对于第i个样品,退化数据为(tj,yij)(i=1,2,…,m;j=1,2,…,n),依据性能退化曲线的趋势,选择适当的退化轨迹模型;
Step 3根据所选择的退化试验方法,选择对应的统计分析方法对试验数据进行分析,得到产品可靠性函数。
3 退化失效混合分布模型
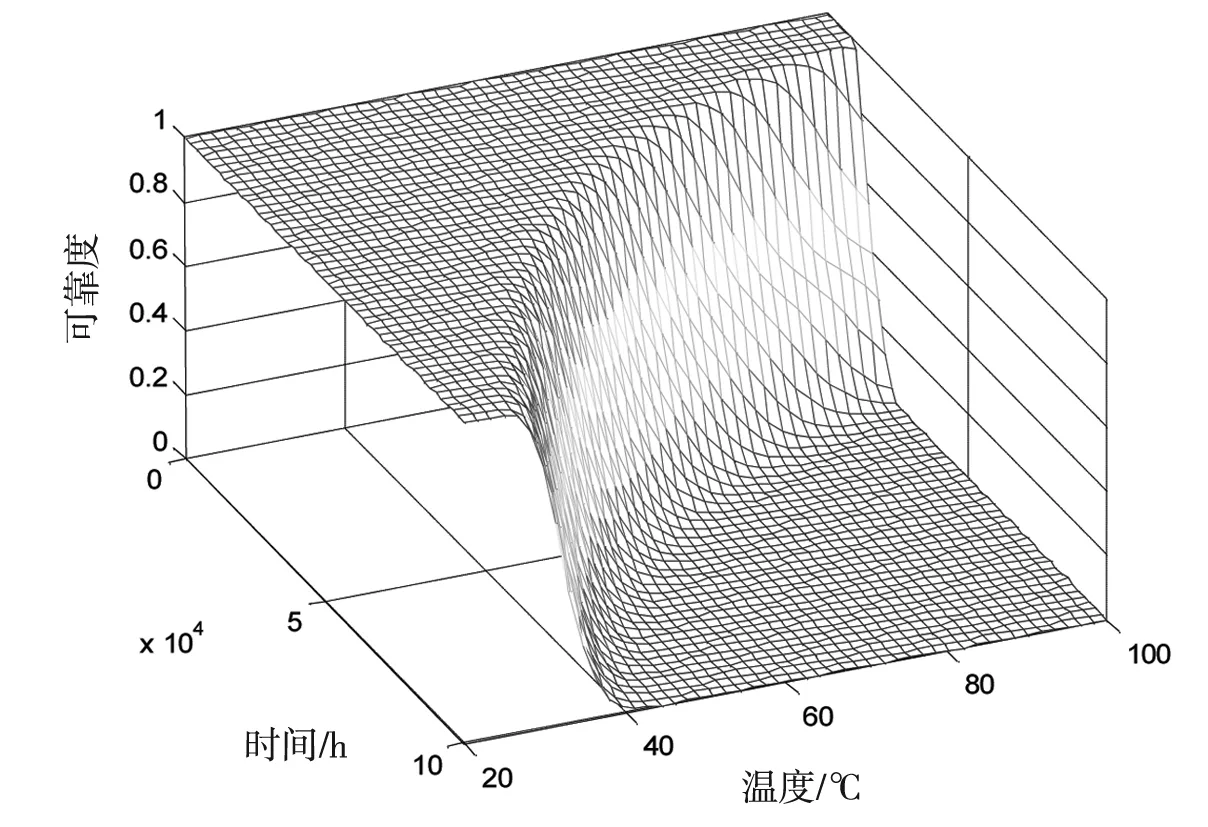
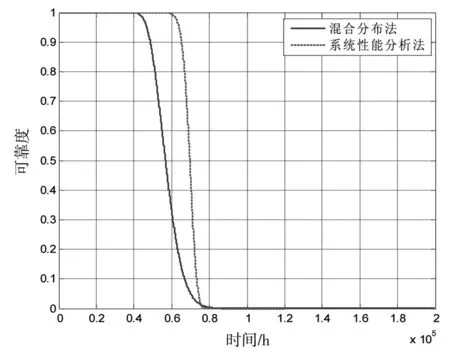
关于混合分布模型,文献[5]是这样定义的:当一总体中每一个个体是k个不同类个体中的某一个,第i个个体在总体中所占比例为pi,诸pi满足0 F(t)=p1F1(t)+p2F2(t)+…+pkFk(t) (1) 对应的可靠度函数为: R(t)=1-F(t)=1-(p1F1(t)+p2F2(t)+…+pkFk(t)) (2) 又由于∑pi=1,则上式变为 R(t)=p1R1(t)+p2R2(t)+…+pkRk(t) (3) 其中Ri(t)=1-Fi(t),而pi的求解成为混合分布模型参数估计的关键所在。 文献[9-10]将混合分布引入由组件分布族确定系统分布的求解中,本文继承这一思想,利用混合分布和关键单元可靠性函数求取系统退化分布模型,具体思路为:组成系统的各关键件的退化失效模型确定后,它们可用同一分布族来描述但参数值不同,此时可使用混合分布的方法来确定系统的分布。基本流程是根据各个分布之间的关系,确定混合参数,再将各可靠性函数与混合参数相乘后求和,即为系统的退化可靠性模型。 Step 1绘制产品的电原理图,而后对系统进行灵敏度仿真分析,得到系统的关键单元; Step 2利用可靠性试验求取关键件的退化失效模型Fi(t)和可靠性函数Ri(t); Step 3将系统关键单元的灵敏度值SRi进行归一化处理,求得对应的pi,具体方法如下: (4) Step 4将pi和Fi(t)代入式(1)可得系统退化失效分布模型: F(t)=p1F1(t)+p2F2(t)+…+pkFk(t) (5) 又由R(t)=1-F(t),∑pi=1可得系统可靠性模型为: R(t)=p1R1(t)+p2R2(t)+…+pkRk(t) (6) 式中:Ri(t)=1-Fi(t),i=1, 2, …,k。 上述流程即为多退化失效模式下基于功能仿真的可靠性建模方法,该方法只需获取底层关键件的退化信息,即可对系统的可靠性进行分析,在实际应用中可降低系统试验的成本,若能与系统可靠性试验信息相结合可进一步提高系统可靠性评估的精度。 图1为一有源低通滤波器电路仿真原理图,要求其在50℃频带宽度要求不低于650kHz,下面以此为例详细介绍基于功能分析的可靠性建模方法。 灵敏度分析采用仿真法实现,只需绘制出该有源滤波器的电原理图(如图1所示)并设置好各元器件的参数, Pspice仿真分析工具就可以给出各元器件关键参数对系统灵敏度的影响,进而就可以确定关键器件及其关键参数。图2为仿真分析结果,从中可以看出关键器件及其关键参数对系统的影响度,将关键器件及其关键参数的影响度进行归一化处理,结果如表1所示。 图1 电路仿真原理图 图2 灵敏度仿真分析结果 由图2可知该有源滤波器的关键元件为:C2、C1、R6、R2、R1、C5和C4,因此选择这几个元件作为系统的关键件,其对应的灵敏度归一化结果如表1所示。 表1 关键器件灵敏度归一化处理结果 对于C2、C1、R6、R2、R1、C5和C4,它们由容值为12pF,10pF和5.6pF的三种电容和阻值为800Ω的电阻构成,这些关键件的失效阈值为标称值的±50%。通过加速试验可以获取这四种器件的性能退化量加速模型,模型如下: (7) (8) (9) (10) 按照本文提出的方法对该有源低通滤波器进行可靠性分析,可以得到5.6pF、10pF、12pF电容及800Ω电阻的归一化灵敏度分别为:0.2841、0.0585、0.2786和0.3788,其可靠度函数为: R(t)=0.2841RC1(t)+0.0585RC2(t)+0.2786RC3(t)+0.3788RR(t)= (11) 又DfC1=2.8,DfC2=5,DfC3=6,DfR=400,并将式(7)~(10)一并代入式(11),可得系统可靠度函数如式(12)所示,该式反映了系统可靠度与时间和环境应力的关系,相应的可靠度曲面如图3所示。 图3 可靠度曲面 (12) 图4 可靠度曲线 当T=50℃对应的可靠度曲线如图4中实线所示,图4中虚线为采用传统方法从系统性能参数的角度对系统可靠性进行分析得到的结果,实线为本文方法在系统功能仿真基础上采用混合分布法得到的结果。从结果看,本文方法要比从系统性能的角度得到结果保守许多,主要原因是:1)分析角度的不同,本文方法是通过底层元件的变化来分析系统的可靠性,它反映了组成系统的关键功能单元对系统可靠性的影响,而传统系统性能分析法则是直接从系统关键性能参数来分析系统的可靠性,它反映了系统自身性能的变化规律;2)从底层关键件参数变化对系统性能参数的影响看,某些关键功能单元的变化使得系统性能参数呈退化趋势,而另外一些则使系统性能参数呈进化趋势,一进一退造成系统性能参数变化的某种对消,这就使得系统性能参数的变化相对稳定,因而造成了系统性能分析法存在一定的“冒进”性。 多退化失效模式下的可靠性建模是比较复杂的问题,本文在现有研究成果基础上,采用系统功能仿真与退化失效分析相结合的方法,给出了多退化失效模式下基于功能仿真的可靠性建模一般程序和方法,为退化型复杂电子产品的可靠性评估提供了一种新思路。4 基于功能仿真的可靠性建模流程
5 实例分析
5.1 灵敏度分析
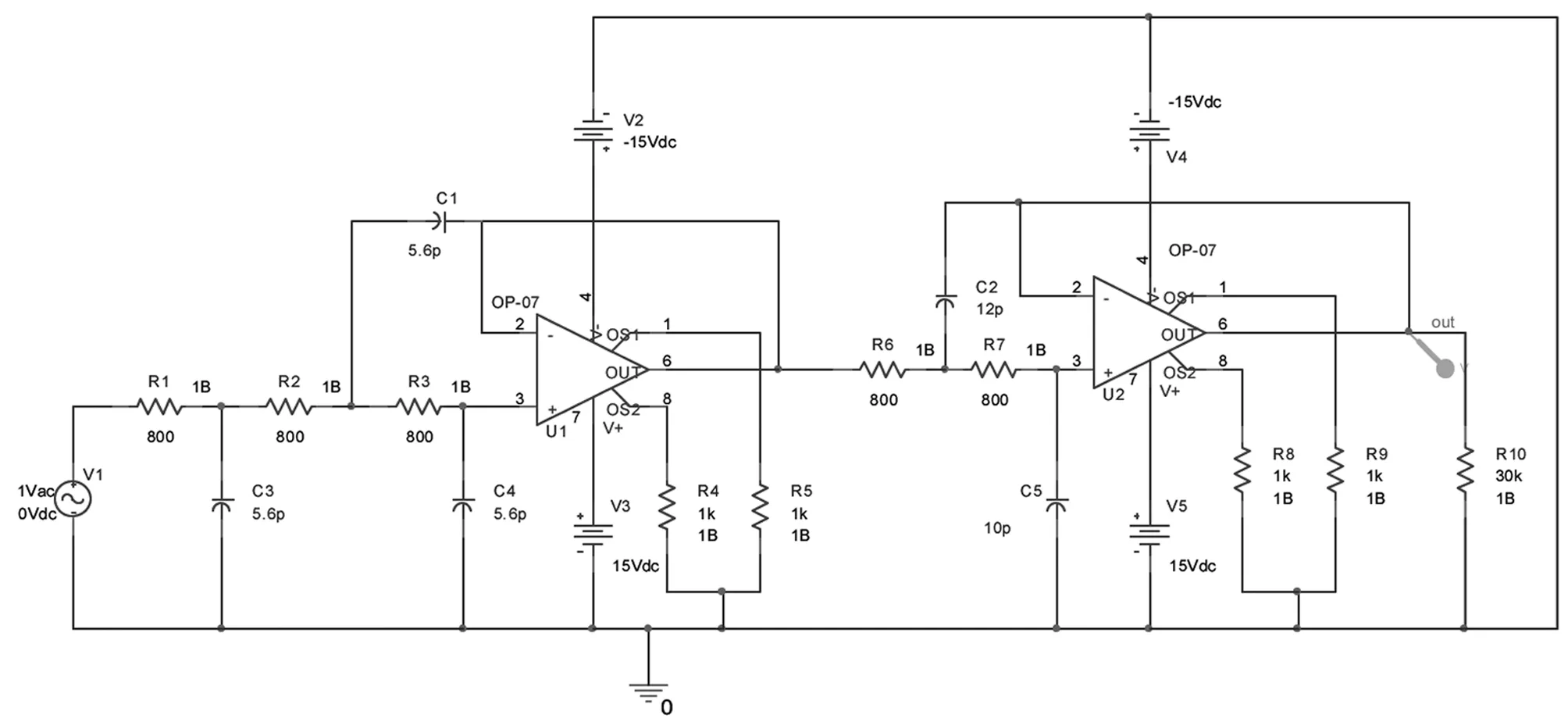
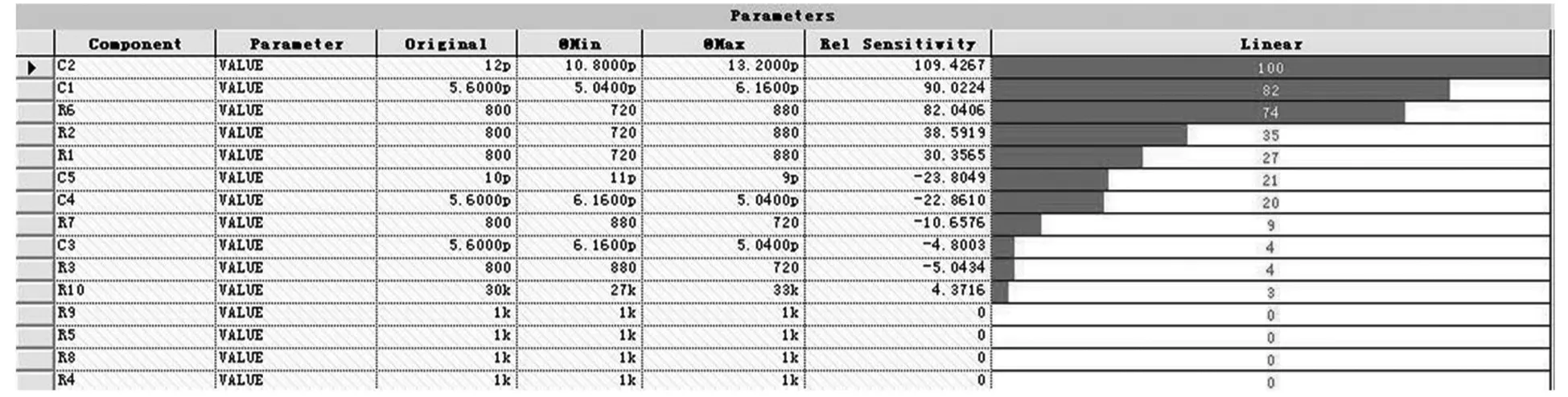
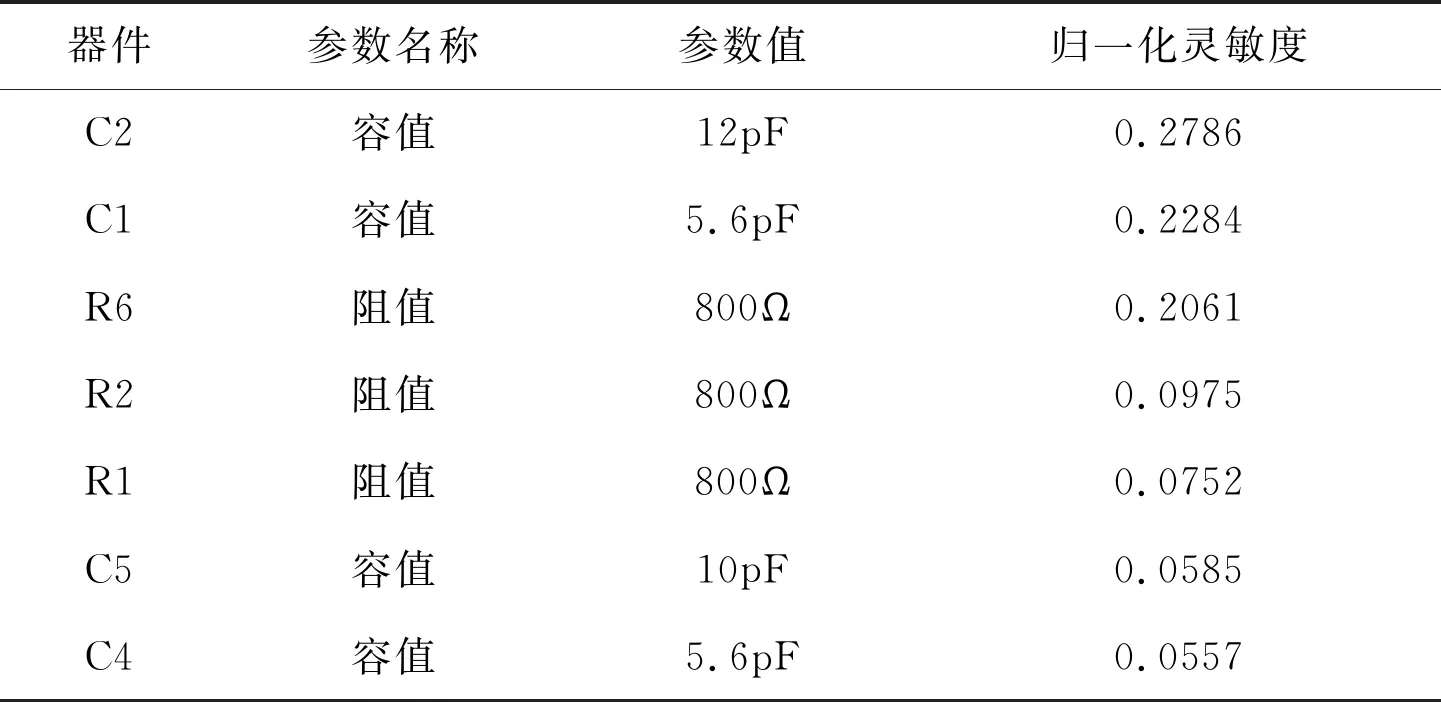
5.2 关键件退化失效模型
5.3 可靠性分析
6 结语

