微分方程与其伴随方程间结构关系探究
吴亚敏
(黄冈师范学院 数学与统计学院,湖北 黄冈 438000)
常系数非齐次线性微分方程的通解,等于对应的常系数齐次线性微分方程的通解,加上常系数非齐次线性微分方程的特解构成[1-2].已有很多专家学者进行研究分析[3-7],本文作者前期对常系数非齐次线性微分方程的特解进行探究,根据右端函数f(x)的三种pm(x),eλxpm(x),eαx[pm1(x)cosβx+pm2(x)sinβx]不同的类型,给出其伴随方程概念,均统一到第一种pm(x)类型,通过对m+1元线性方程组的求解,得到了常系数非齐次线性微分方程的特解.本文将继续深入研究,探究微分方程与其伴随方程间的结构关系.
1 主要定理
1.1 二阶常系数线性微分方程
方程
y″+py′+qy=eλxpm(x)
(1)
的伴随方程为
Q″(x)+T′(λ)Q′(x)+T(λ)Q(x)=pm(x)
(2)

设
Z″(x)+T′(-λ)Z′(x)+T(-λ)Z(x)=eλxpm(x)
(3)
y″+py′+qy=pm(x)
(4)
在方程(1)中,令y=eλxQ(x),求其各阶导数代入方程(1),整理得到方程(2).
用eλx乘以方程(4)得eλx(y″+py′+qy)=eλxpm(x),令Z(x)=eλxy,求其各阶导数,代入整理得到方程(3).
定义1若二阶常系数非齐次线性微分方程(2)是微分方程(1)的伴随方程,则称微分方程(1)是微分方程(2)的伴随前的微分方程.
显然,伴随前的方程(1)的自由项中含有eλx因子,其伴随方程(2)的自由项中不含eλx因子.当λ=0时,以上四个微分方程是同一个微分方程.
方程(1)、(2)、(3)、(4)对应的齐次微分方程的特征方程为
T(r)=r2+pr+q=0
(5)
T1(r)=r2+T′(λ)r+T(λ)=0
(6)
T2(r)=r2+T′(-λ)r+T(-λ)=0
(7)
T(r)=r2+pr+q=0
定理1特征多项式T(r),T1(r),T2(r)满足下列关系:
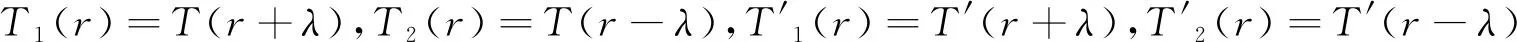
证明
T1(r-λ)=(r-λ)2+(2λ+p)(r-λ)+λ2+pλ+q=r2+pr+q=T(r),
T2(r+λ)=(r+λ)2+(-2λ+p)(r+λ)+λ2-pλ+q=r2+pr+q=T(r),
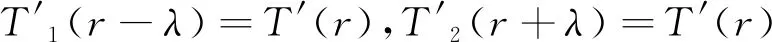

推论2若ri是特征方程(5)的特征根,则ri∓λ分别是特征方程(6)、(7)的特征根.
推论3若r1,r2是微分方程(1)或(4)的特征根,则T(r)=(r-r1)(r-r2),T1(r)=(r-r1+λ)(r-r2+λ),T2(r)=(r-r1-λ)(r-r2-λ)
推论4微分方程(1)、(3)分别是微分方程(2)、(4)的伴随前的方程.
推论5伴随前的方程(1)、(3)分别与其伴随方程(2)、(4)对于同一个λ是一一对应的.
定理2若r1,r2是特征方程(5)的特征根,则微分方程(1)、(2)、(3)、(4)对应的齐次微分方程的通解分别为
(1)当r1≠r2时,Y(x)=c1er1x+c2er2x,Q(x)=c1e(r1-λ)x+c2e(r2-λ)x=e-λxY(x),
Z(x)=c1e(r1+λ)x+c2e(r2+λ)x=eλxY(x),Y(x)=c1er1x+c2er2x
(2)当r1=r2=r时,Y(x)=(c1+c2x)erx,Q(x)=(c1+c2x)e(r-λ)x=e-λxY(x),
Z(x)=(c1+c2x)e(r+λ)x=eλxY(x),Y(x)=(c1+c2x)erx
(3)当r=α±βi时,Y(x)=eαx(c1cosβx+c2sinβx),Q(x)=e(α-λ)x(c1cosβx+c2sinβx)=e-λxY(x),
Z(x)=e(α+λ)x(c1cosβx+c2sinβx)=eλxY(x),Y(x)=eαx(c1cosβx+c2sinβx)
推论6Y(x)=eλxQ(x)或Q(x)=e-λxY(x);Z(x)=eλxY(x)或Y(x)=e-λxZ(x)
定理3若r1,r2是特征方程(5)的特征根,Q*(x),y*(x)分别是微分方程(2)、(4)的特解,则微分方程(1)、(2)、(3)、(4)的通解分别为
(1)当r1≠r2时,y=c1er1x+c2er2x+eλxQ*(x),Q=c1e(r1-λ)x+c2e(r2-λ)x+Q*(x),
Z=c1e(r1+λ)x+c2e(r2+λ)x+eλxy*(x),y=c1er1x+c2er2x+y*
(2)当r1=r2=r时,y=(c1+c2x)erx+eλxQ*(x),Q=(c1+c2x)e(r-λ)x+Q*(x),
Z=(c1+c2x)e(r+λ)x+eλxy*(x),y=(c1+c2x)erx+y*(x)
(3)当r=α±βi时,y=eαx(c1cosβx+c2sinβx)+eλxQ*(x),Q=e(α-λ)x(c1cosβx+c2sinβx)+Q*(x),
Z=e(α+λ)x(c1cosβx+c2sinβx)+eλxy*(x),y=eαx(c1cosβx+c2sinβx)+y*(x)
推论7y(x)=eλxQ(x)或Q(x)=e-λxy(x);Z(x)=eλxy(x)或y(x)=e-λxZ(x)
1.2 n阶常系数线性微分方程
方程
p0y(n)+p1y(n-1)+…+pn-1y′+pny=eλxpm(x)
(8)
的伴随方程为
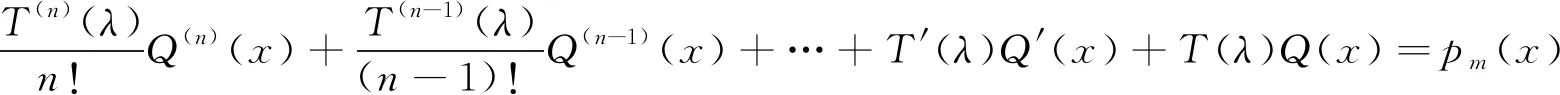
(9)
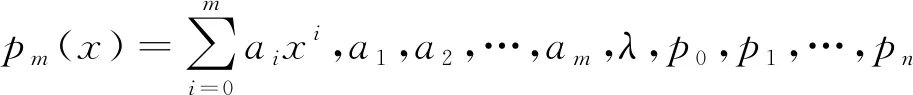

(10)
p0y(n)+p1y(n-1)+…+pn-1y′+pny=pm(x)
(11)
在方程(8)中,令y=eλxQ(x),求其各阶导数代入方程(8),整理得到方程(9).
用eλx乘以方程(11)得到方程eλx(p0y(n)+p1y(n-1)+…+pn-1y′+pny)=eλxpm(x),令Z(x)=eλxy,求其各阶导数代入,整理得到方程(10).
定义2若n阶常系数非齐次线性微分方程(9)是微分方程(8)的伴随方程,则称微分方程(8)是微分方程(9)的伴随前的微分方程.
显然,伴随前的方程(8)的自由项中含有eλx因子,其伴随方程(9)的自由项中不含eλx因子.当λ=0时,以上四个微分方程是同一个微分方程.
方程(8)、(9)、(10)、(11)对应的齐次微分方程的特征方程为
T(r)=p0rn+p0rn-1+…+pn-1r+pn=0
(12)
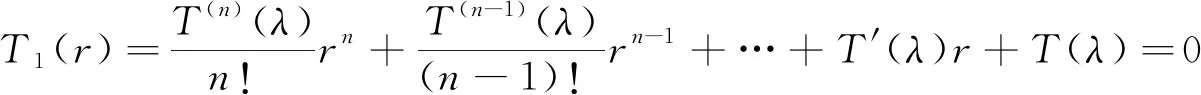
(13)

(14)
T(r)=p0rn+p0rn-1+…+pn-1r+pn=0
定理4特征多项式T(r),T1(r),T2(r)满足下列关系:
T1(r-λ)=T(r),T2(r+λ)=T(r),
T1(k)(r-λ)=T(k)(r),T2(k)(r+λ)=T(k)(r),1≤k≤n,
或T1(r)=T(r+λ),T2(r)=T(r-λ),
T1(k)(r)=T(k)(r+λ),T2(k)(r)=T(k)(r-λ),1≤k≤n
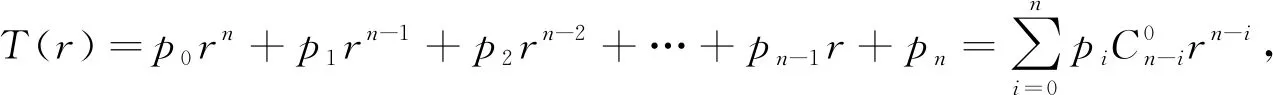
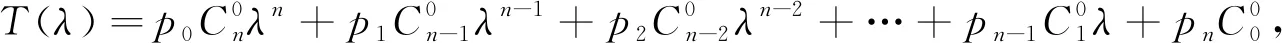
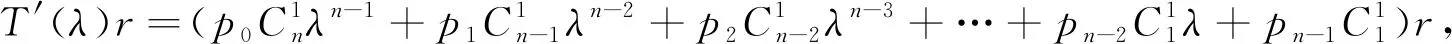

……
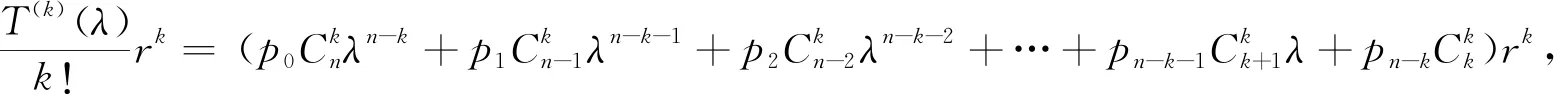
……
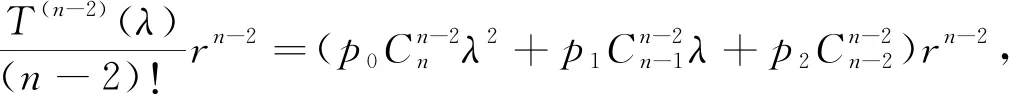
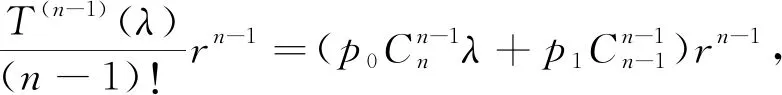
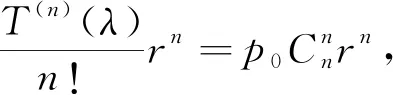
以上各项全部相加,按p0,p1,p2,…,pn提取公因式得:

=p0(λ+r)n+p1(λ+r)n-1+p2(λ+r)n-2
+…+pk(λ+r)n-k…+
pn-2(λ+r)2+pn-1(λ+r)+pn=T(r+λ)
同理可证T2(r)=T(r-λ)
在T1(r)=T(r+λ),T2(r)=T(r-λ)两边对r求k阶导数得
T1(k)(r)=T(k)(r+λ),T2(k)(r)=T(k)(r-λ),1≤k≤n,
推论8T1(-λ)=T(0)=pn,T2(λ)=T(0)=pn,
推论9若ri是特征方程(12)的特征根,则ri∓λ分别是特征方程(13)、(14)的特征根.
推论10若r1,r2,…,rn是微分方程(8)或(11)的特征根,则
推论11微分方程(8)、(10)分别是微分方程(9)、(11)的伴随前的方程.
推论12伴随前的方程(8)、(10)分别与其伴随方程(9)、(11)对于同一个λ是一一对应的.
定理5若r1,r2,…,rn是特征方程(12)的特征根,则微分方程(8)、(9)、(10)、(11)对应的齐次微分方程的通解分别为
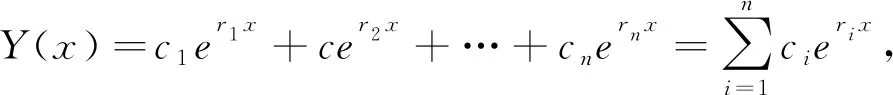
Q(x)=c1e(r1-λ)x+c2e(r2-λ)x+…+cne(rn-λ)x=e-λxY(x),
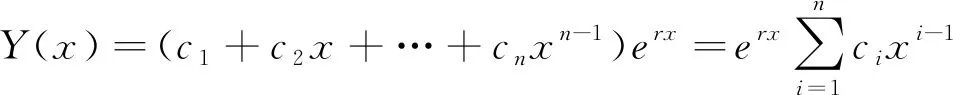
Q(x)=(c1+c2x+…+cnxn-1)e(r-λ)x=e-λxY(x),
(3)当r1=r2=…=rk=r,rk+1≠…≠rn时,
Y(x)=(c1+c2x+…+ckxk-1)erx+ck+1erk+1x+…+cnernx,
Q(x)=(c1+c2x+…+ckxk-1)e(r-λ)x+ck+1e(rk+1-λ)x+…+cne(rn-λ)x,
Z(x)=(c1+c2x+…+ckxk-1)e(r+λ)x+ck+1e(rk+1+λ)x+…+cne(rn+λ)x,
Y(x)=(c1+c2x+…+ckxk-1)erx+ck+1erk+1x+…+cnernx
(4)当r1,2=r3,4=…=rn-1.n=α±βi,n=2k时,
Q(x)=e(α-λ)x[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]=e-λxY(x),
Z(x)=e(α+λ)x[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]=eλxY(x),
(5)当r1,2=r3,4=…=r2k-1,2k=α±βi,r2k+1≠…≠rn时,
Y(x)=eαx[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]+c2k+1er2k+1x+…+cnernx,
Q(x)=e(α-λ)x[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]+c2k+1e(r2k+1-λ)x+…+cne(rn-λ)x,
Z(x)=e(α+λ)x[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]+c2k+1e(r2k+1+λ)x+…+cne(rn+λ)x,
Y(x)=eαx[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]+c2k+1er2k+1x+…+cnernx
……
推论13Y(x)=eλxQ(x)或Q(x)=e-λxY(x);Z(x)=eλxY(x)或Y(x)=e-λxZ(x)
定理6若r1,r2,…,rn是特征方程(12)的特征根,Q*(x),y*(x)分别是微分方程(9)、(11)的特解,则微分方程(8)、(9)、(10)、(11)的通解分别为
(1)当r1≠r2≠…≠rn时,
y=c1er1x+c2er2x+…+cnernx+eλxQ*(x),
Q=c1e(r1-λ)x+c2e(r2-λ)x+…+cne(rn-λ)x+Q*(x),
Z=c1e(r1+λ)x+c2e(r2+λ)x+…+cne(rn+λ)x+eλxy*(x),
y=c1er1x+c2er2x+…+cnernx+y*(x)
(2)当r1=r2=…=rn=r时,
y=(c1+c2x+…+cnxn-1)erx+eλxQ*(x),Q=(c1+c2x+…+cnxn-1)e(r-λ)x+Q*(x),
Z=(c1+c2x+…+cnxn-1)e(r+λ)x+eλxy*(x),y=(c1+c2x+…+cnxn-1)erx+y*(x)
(3)当r1=r2=…=rk=r,rk+1≠…≠rn时,
y=(c1+c2x+…+ckxk-1)erx+ck+1erk+1x+…+cnernx+eλxQ*(x),
Q=(c1+c2x+…+ckxk-1)e(r-λ)x+ck+1e(rk+1-λ)x+…+cne(rn-λ)x+Q*(x),
Z=(c1+c2x+…+ckxk-1)e(r+λ)x+ck+1e(rk+1+λ)x+…+cne(rn+λ)x+eλxy*(x),
y=(c1+c2x+…+ckxk-1)erx+ck+1erk+1x+…+cnernx+y*(x)
(4)当r1,2=r3,4=…=rn-1,n=α±βi,n=2k时,
y=eαx[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]+eλxQ*(x),
Q=e(α-λ)x[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]+Q*(x),
Z=e(α+λ)x[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]+eλxy*(x),
y=eαx[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]+y*(x)
(5)当r1,2=r3,4=…=r2k-1,2k=α±βi,r2k+1≠…≠rn时,
y=eαx[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]+c2k+1er2k+1x+…+cnernx+eλxQ*(x),
Q=e(α-λ)x[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]+c2k+1e(r2k+1-λ)x+…+cne(rn-λ)x+Q*(x),
Z=e(α+λ)x[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]+c2k+1e(r2k+1+λ)x+…+cne(rn+λ)x+eλxy*(x),
y=eαx[(c1+c2x+…+ckxk-1)cosβx+(d1+d2x+…+dkxk-1)sinβx]+c2k+1er2k+1x+…+cnernx+y*(x)
……
推论14y(x)=eλxQ(x)或Q(x)=e-λxy(x);Z(x)=eλxy(x)或y(x)=e-λxZ(x)
2 应用实例
例1求方程y″-4y′+4y=8x2+e2x+sin2x+cos2x的通解
解(1)y″-4y′+4y=0的通解
T(r)=r2-4r+4=0,r1=r2=2,Y(x)=(c1+c2x)e2x
(2)y″-4y′+4y=8x2+e2x+sin2x的特解
第一,y″-4y′+4y=8x2的特解y1,其伴随微分方程与伴随前的方程相同.
第二,y″-4y′+4y=e2x的特解y2,其伴随微分方程为
第三,y″-4y′+4y=sin2x,y″-4y′+4y=cos2x的特解y31,y32
y″-4y′+4y=e2ix的伴随微分方程为
(3)y″-4y′+4y=8x2+e2x+sin2x+cos2x的通解为
例2设y‴-y″-y′+y=eλx(1+x+x2)
(1)求y‴-y″-y′+y=1+x+x2的伴随前的微分方程及其通解
(2)求y‴-y″-y′+y=eλx(1+x+x2)的通解
(3)求方程y‴-y″-y′+y=(1+x+x2)(1+e2x+sinx+cosx)的通解
解(1)y‴-y″-y′+y=1+x+x2的伴随前的微分方程及其通解
不难求得y‴-y″-y′+y=1+x+x2的通解为y=(c1+c2x)ex+c3e-x+6+3x+x2.
eλx(y‴-y″-y′+y)=eλx(1+x+x2),令Z(x)=eλxy,求其导数后,代入整理得
Z‴(x)-(3λ+1)Z″(x)+(3λ2+2λ-1)Z′(x)+(-λ3-λ2+λ+1)Z(x)=eλx(1+x+x2)
或根据推论12,得y‴-y″-y′+y=1+x+x2的伴随前的微分方程为
根据推论14,其通解为
Z(x)=eλxy=(c1+c2x)e(1+λ)x+c3e(-1+λ)x+eλx(6+3x+x2)
(2)y‴-y″-y′+y=eλx(1+x+x2)的通解
令y=eλxQ(x),求其导数后,代入上述方程整理得伴随微分方程
Q‴(x)+(3λ-1)Q″(x)+(3λ2-2λ-1)Q′(x)+(λ3-λ2-λ+1)Q(x)=1+x+x2,
的通解为
(3)y‴-y″-y′+y=(1+x+x2)(1+e2x+sinx+cosx)的通解为
1)y‴-y″-y′+y=0的通解为Y(x)=(c1+c2x)ex+c3e-x
2)由(2)得,当λ=0时,y‴-y″-y′+y=1+x+x2与其伴随微分方程相同
其中T=1,T′=-1,T″=-2
通解y=(c1+c2x)ex+c3e-x+6+3x+x2
特解y1=6+3x+x2;
当λ=2时,y‴-y″-y′+y=e2x(1+x+x2)伴随微分方程为
其中T=3,T′=7,T″=10,
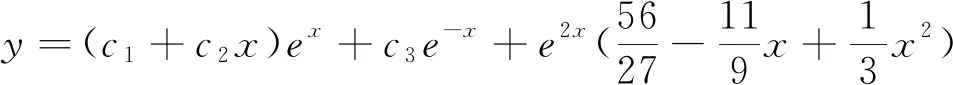
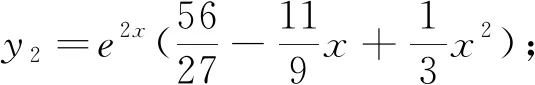
当λ=i时,y‴-y″-y′+y=eix(1+x+x2)伴随微分方程为
Q‴+(-1+3i)Q″+(-4-2i)Q′+(2-2i)Q=1+x+x2,
其中T=2-2i,T′=-4-2i,T″=-2+6i
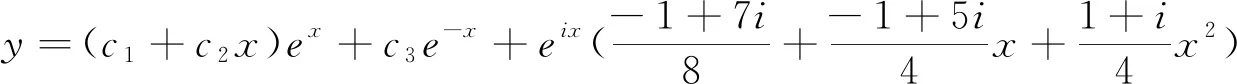
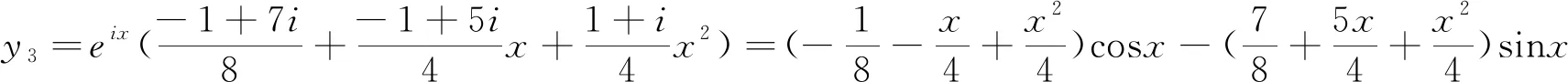
y3的实部y31与虚部y32分别是方程
y‴-y″-y′+y=(1+x+x2)cosx,y‴-y″-y′+y=(1+x+x2)sinx的特解.
3)y‴-y″-y′+y=(1+x+x2)(1+e2x+sinx+cosx)的通解
y=(c1+c2x)ex+c3e-x+y1+y2+y31+y32=(c1+c2x)ex+c3e-x+6+3x+x2
对于求y‴-y″-y′+y=1+x+x2的伴随前的微分方程和其通解,其伴随方程与参变量λ无关,问题容易解决.而对于方程y‴-y″-y′+y=eλx(1+x+x2),求参变量λ的微分方程方程和其通解,其伴随方程与参变量λ有关,问题也能解决.这样为一个确定的线性系统讨论研究,提供了一条很有帮助的路径.
3 结论
若微分方程(1)或(8)对应的齐次微分方程的通解为Y(x),则其伴随微分方程(2)或(9)对应的齐次微分方程的通解为e-λxY(x),反之亦然.若伴随微分方程(4)或(11)对应的齐次微分方程的通解为Y(x),则微分方程(3)或(10)对应的齐次微分方程的通解为eλxY(x),反之亦然.
若微分方程(1)或(8)的通解为Y(x)+eλxQ*(x),则其伴随微分方程(2)或(9)通解为e-λxY(x)+Q*(x),反之亦然.若微分方程(3)或(10)的通解为eλxY(x)+eλxy*(x),则其伴随微分方程(4)或(11)通解为Y(x)+y*(x),反之亦然.其中Y(x)是伴随微分方程(4)或(11)对应的齐次微分方程的通解,Q*(x)是伴随微分方程(2)或(9)的特解,y*(x)是伴随微分方程(4)或(11)的特解.

