最优法Hilbert滤波器与小波变换融合的功率测量算法
杨庆江, 王卫鑫, 杨 硕
(黑龙江科技大学 电子与信息工程学院, 哈尔滨 150022)
0 引 言
在电力系统的运行过程中,电网需要提供有功电能和无功电能,有功电能反映的是单向转换成其他能量的部分,无功电能是电场能量和磁场能量交换的部分[1]。有功功率的准确测量是电量统计和电费计算的基本前提,无功功率是减少电力网络的损耗和确保电网安全的重要数据[2]。因此,功率的准确测量对电力公司和电力用户十分重要,对于功率测量算法的研究具有重要意义。J. Munkert[3]在频域分析的基础上,提出了一种可用于信号含有谐波分量的定义方法。邱帅兵等[4]指出傅里叶变换法适用于畸变信号的功率测量,但在计算时需要大量的寄存器存储变量,计算量较大且计算时间较长,实时性也比较差。王薇等[5]研究了数字移相法测量来无功功率,具有很好的实时性,但其在测量含有谐波的信号时测量误差较大。曹峰等[6]提出了Hilbert变换算法,适用在正弦与非正弦的电路系统中测量含有谐波信号的功率,希尔伯特变换法要求较高的实时系统,算法较复杂,应用不够快捷简便。为了进一步提高无功功率的测量精度,笔者在Budeanu对功率进行定义的基础上,采用最优法设计Hilbert数字滤波器与小波变换融合的功率测量算法对有功功率和无功功率进行测量,以提高其测量精度。
1 Hilbert数字滤波器
1.1 理想Hilbert数字滤波器
Hilbert滤波器单位冲激响应的频域形式为:
式中,ω——频率。
幅值为|Hd(ω)|=1,相角为:
由以上可知,Hilbert滤波器的幅频特性是全通滤波器,信号经过Hilbert变换后,它的正频率部分和负频率部分别作-90°和+90°相移[7]。
1.2 最优法设计的Hilbert数字滤波器
假设N是奇数,滤波器的频率响应是Hd(ejω) ,逼近加权函数是W(ω),用线性FIR相位数字滤波器的H(ω)为逼近函数[8],则逼近误差函数为
E(ω)=W(ω)[Hd(ejω)-H(ω)]。
令δ=max{|E(ω)|},从最优法的基本原理考虑,该设计法最重要的环节是选择合适的H(ω)使δ尽可能的小,即可得到最合适的单位脉冲响应h(n),则所求滤波器的频率响应为
式中,ωl——截止频率。
最优法设计的滤波器是等波纹的[9],并且该设计方法采用最大误差最小的准则来逼近理想的Hilbert数字滤波器,既能获得严格线性相位,又有很好的衰减特性,对通、阻带边界频率以及对纹波特性都有较好的控制[10]。最优法设计的Hilbert数字滤波器的相频和幅频如图1所示。

图1 Hilbert数字滤波器的频率特性Fig. 1 Frequency characteristics of Hilbert digital filter
2 正交小波分解
将L2(R)按以下空间分解[10]
式中:L2(R)——平方可积函数空间;
J——任意设定的尺度;
Wj、VJ——尺度空间。
若f(t)∈L2(R),则有
式中:cj,k——尺度系数;
dj,k——小波系数;
φj,k(t)——尺度函数;
ψj,k(t)——小波函数。
当J→∞时
(1)
则有
(2)
式(1)中,等号右边第一部分是信号在小波空间Wj上的投影,它从细节上表示了信号,另一部分是信号在尺度空间VJ上的投影,它从整体上表示了细节。
3 功率测量算法
利用最优法设计的Hilbert数字滤波将求各次谐波电压分别移相四分之一周期后的电压U(t-T/4),U(n)、I(n)、U(t-T/4)(n)分别表示U(t)、I(t)、U(t-T/4)的采样信号,在T内进行2N次采样,分别进行正交小波分解:
利用φJ,K(t)和ψj,k(t)之间的正交性,有:
电压有效值
电流有效值
有功功率

PJ表示小波分解后最低频带的有功功率值,Pj表示小波分解后最高频带的有功功率值。
无功功率QB计算公式

QBJ表示最低频带的无功功率值,QBj最高频带的无功功率值。由奈奎斯特采样定理可知,为了使恢复的模拟信号保留信号原本的信息,采样频率必须要大于或等于2倍模拟信号频率,在这里对于基波信号如果在一个周期内进行128次采样就可以得到64次谐波[11]。小波分解原理是每层分解都是针对低频部分进行的,如果是第一次分解则对信号进行分解即电压或电流信号,对频带的二等分是按照所能分析的最高频率进行的,因此128次的采样时根据最高频率3.2 kHz进行的,小波分解过程如图2所示。

图2 小波分解过程Fig. 2 Wavelet decomposition process
4 仿真结果与分析
4.1 数据模型
小波分解后的频带和谐波次数如表1所示,各次电压电流如表2所示。
仿真实验所采用的电压信号和电流信号为:
式中:f——频率,文中f=50 Hz;
θk——电流信号的初相位。

表1 频带和谐波次数

表2 电压、电流参数
4.2 仿真模型
对采样后的电压U(n)、电流I(n)和U(t-T/4)(n)进行5层小波分解运算。由以上介绍的算法原理及分析过程可得有效值、有功功率、无功功率计算的基本流程如图3、4所示。
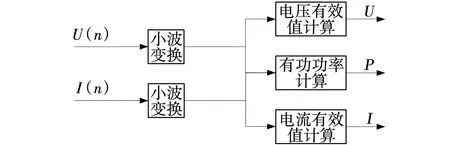
图3 有效值及有功功率测量流程 Fig. 3 Flow of effective value and active power measurement

图4 无功功率测量流程Fig. 4 Flow of reactive power measurement
根据最优法设计的Hilbert数字滤波器及小波变换后的功率算法公式,在Matlab/Simulink软件中搭建无功功率和无功率测量的仿真模型如图5所示,其中,小波变换函数选用Haar小波函数。

图5 无功功率测量的仿真模型Fig. 5 Simulation model for reactive power measurement
4.3 结果分析
表3为给定参数的电压和电流通过尺度小波分解后在各小波层上计算所得的有功和无功功率。各种算法的仿真结果如表4所示。各小波层上的有功及无功功率的代数和分别等于表3中用小波变换结合最优法滤波器算法所求得的有功功率和无功功率。
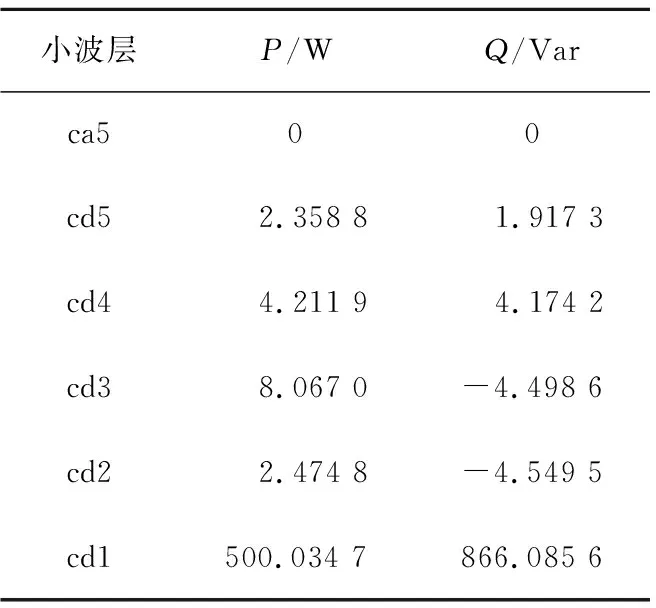
表3 小波层功率
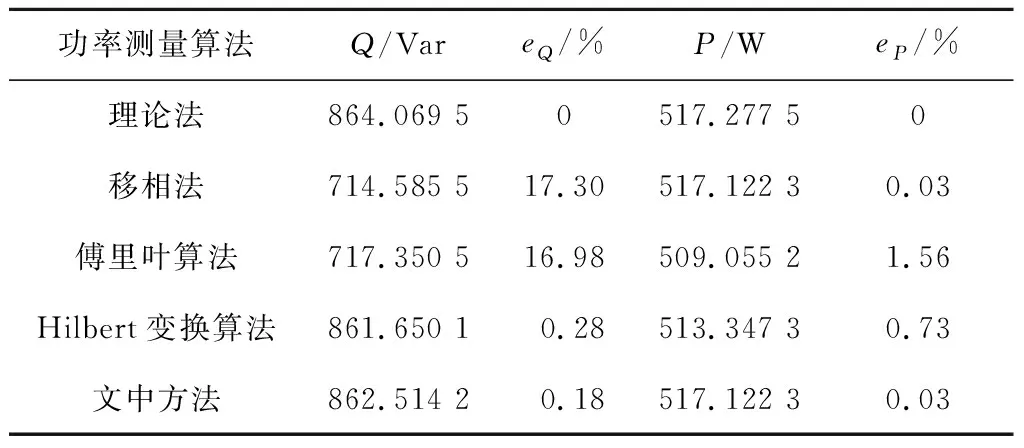
表4 各种算法的仿真结果
从表4可以看出,在有功功率的测量方面,移相法和最优法数字滤波器与小波变换相结合的功率测量算法的误差都很小,傅里叶变换测量的误差最大,Hilbert变换算法次之。从无功功率的测量来看,最优法数字滤波器与小波变换相结合的功率测量算法的误差最小,Hilbert变换算法测量误差次之,傅里叶变换和数字移相算法的测量误差较大。
5 结束语
利用最优法的最大误差最小准则逼近的方法得到了Hilbert数字滤波器,该滤波器既能获得严格线性相位,又有很好的衰减特性,对通、阻带边界频率以及对纹波特性都有较好的控制,利用数字滤波器对电压信号进行90°相移。采用正交小波分解将相移90°后的电压信号和电流信号在5层小波层上进行了分解,分解后在各个小波层上计算了有功和无功功率。选取了含有谐波的信号模型并利用Matlab/Simulink建立了仿真模型,完成了对文中算法及目前存在的其他几种算法的仿真,结果显示:文中算法将有功功率的测量误差控制在0.03%,无功功率的测量误差控制在0.18%,降低了功率测量的误差,对实际的功率测量以及后续功率研究具有参考价值。

