基于ADAMS的碟盘振动切削破碎煤岩机构的动力学特性

刘春生， 那洪亮， 韩德亮

(1.黑龙江科技大学， 哈尔滨 150022； 2.黑龙江科技大学 机械工程学院， 哈尔滨 150022)

0 引 言

振动切削破岩机构的动力学特性是影响其工作性能的重要因素，通过动力学仿真软件研究其动力特性，对分析其工作性能具有重要意义。张东升等[1]建立了冲击破岩掘进机的虚拟样机模型，指出了两种不利工况下掘进工作臂各铰点的受力情况。任斌等[2]利用UG和ADAMS软件模拟水平定向钻牙轮扩孔器在不同钻进参数情况的牙齿上某一点位移、速度、加速度及空间运动轨迹等数据，得出牙轮扩孔器扩孔过程运动规律。侯祥林等[3]建立了单轴惯性振动机的动力学仿真模型并研究了振动机在起动和停车过程中偏心块转动量、振动机位移与速度变量随时间的变化规律。梁国栋等[4]利用ADAMS软件研究了振动破碎机机体的振动情况、运动轨迹以及同步稳定性。鲁云松等[5]建立了单自由度振动筛模型和二自由度振动筛的动力学仿真模型，获得了倾角、位移及加速度的变化规律。刘春生等[6-7]通过理论分析构建了碟盘刀具振动切削煤岩的理论力学模型，指出了其破碎煤岩的载荷特性。利用ADAMS软件模拟机构工作过程的运动情况，可以分析机构的动力学特性，笔者通过ADAMS软件建立碟盘振动切削破碎煤岩机构的动力学仿真模型与理论模型，研究不同激振频率、弹簧刚度和偏心块质量对机构的固有频率、振幅与最大激振力的影响。

1 虚拟样机模型

1.1 模型的建立

为提高动力学仿真的简便性与运行效率，使用UG软件创建零部件三维模型时，在不影响机构性能的前提下，将具有固定工作位置和配合关系的零件视为一体，略去轴套、螺栓等定位件和连接件，碟盘振动切削破碎煤岩机构的虚拟样机模型见图1。

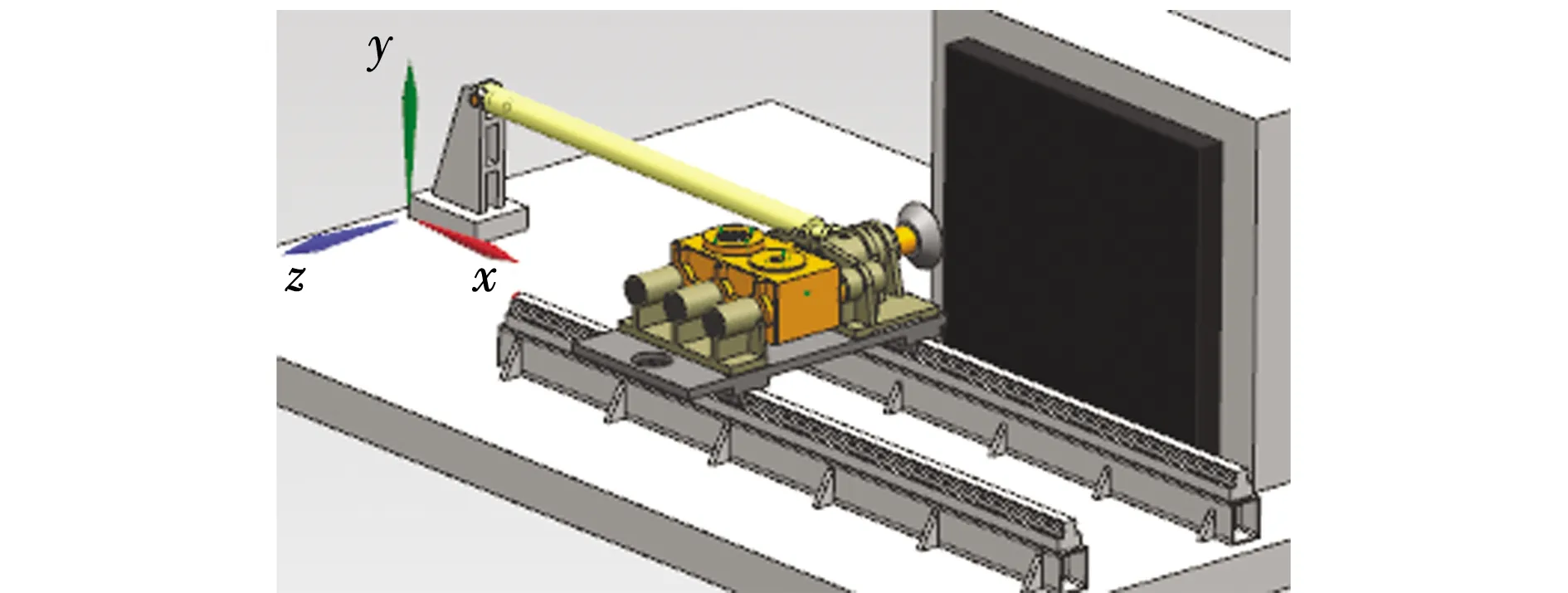
图1 虚拟样机模型Fig. 1 Virtual prototype model

在ADAMS中导入图1模型的Parasolid 格式文件，统一ADAMS软件与UG软件对应物理量的单位。根据具体工况对机构模型施加约束条件与输入相关参数。

(1)材料属性

ADAMS软件可自动识别导入模型的零部件体积，根据材料密度等属性自动计算出零部件的质心、质量、转动惯量等物理参数。模型中偏心块材料采用40Cr，密度为7.87×103kg/m3，其余零部件材料选用45#钢，密度为7.89×103kg/m3。

(2)约束条件

机构的轴向振动为激振箱在偏心块的惯性力驱动下沿轴向往复振动，故将偏心块所在的两根齿轮轴设为齿轮副，使其同速反向运动，齿轮与箱体间设为旋转副，激振箱与前、后支座间设为移动副，并通过弹簧阻尼器连接。前、后支座与底板、轴承与激振箱体等固定连接部分通过布尔求和运算合并为一体。

(3)驱动函数

为使机构能够按照一定的规律运动，对未受运动副约束的自由度进行运动定义。机构振动时，传动比为1的两个齿轮等速反向旋转，进而带动齿轮轴上的偏心块转动，驱动激振箱振动。因此，将齿轮轴的旋转副设置成旋转形式的驱动函数为

STEP(time，t1，n1d，t2，n2d)。

驱动函数转速从t1到t2的时间内由n1(°)/s增加到n2(°)/s，保持n2(°)/s的转速持续转动。

1.2 模型参数的确定

机构载荷的添加主要考虑激振箱沿轴向振动的弹簧作用，故在激振箱体的导向轴与前、后支座的套筒间添加弹簧，使用ADAMS软件中拉压弹簧阻尼器代替实物弹簧，通过改变弹簧阻尼模块的参数来改变弹簧的刚度。

弹簧刚度

式中:G——弹簧材料的切变模量，Pa；

d0——弹簧丝直径，m；

δ——绕曲比，δ=d1/d0；

d1——弹簧中径，m；

n0——弹簧有效圈数。

采用65 Mn圆形截面圆柱螺旋压缩弹簧，d0为10～18 mm，不同规格弹簧对应参数见表1。

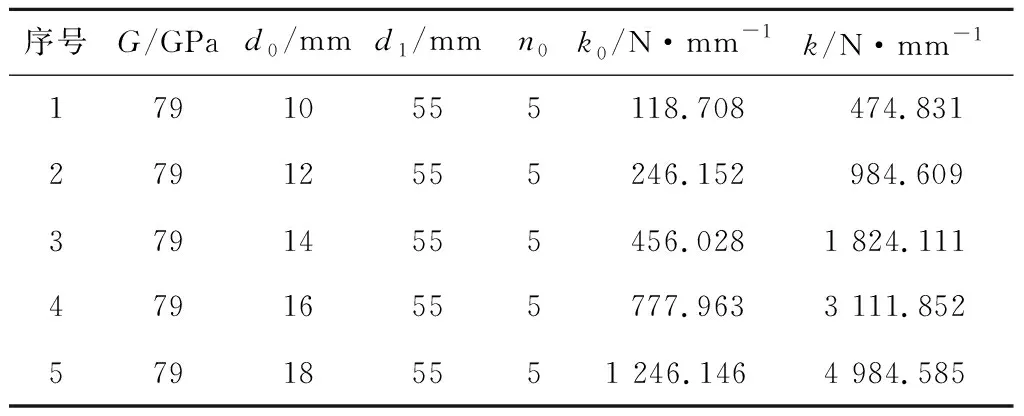
表1 弹簧参数

激振箱在振动过程所受阻尼包括弹簧材料的内部摩擦阻尼和导向轴与套筒之间的干摩擦阻尼，施加驱动时需等效为黏性阻尼。根据文献[8]，单根弹簧内部摩擦阻尼的等效阻尼系数为

式中,η——材料的损耗因子,对于内部摩擦阻尼，η为常量,金属等材料的η=0.001～0.010[7]，文中取η=0.005 5；

ω——激振角频率，rad/s。

激振箱导向轴与套筒之间干摩擦阻尼的等效阻尼系数[7]为

式中:μ——两接触面之间的摩擦系数，μ=0.15；

FN——两接触面之间的垂直压力，激振箱重力，N；

A——激振箱的振幅，mm。

激振频率远超固有频率时，激振箱振幅为

式中:m0——单枚偏心块质量，kg；

r0——偏心半径，mm，模型中r0=42 mm；

m——振动体总质量，kg。

激振箱的等效阻尼系数为

c=cf+4c0。

(1)

设置完模型的参数及约束后，输入不同工况对应的参数，分析输出位移响应、激振力等曲线表征的动力学特性。

2 不同参数下机构的动力学特性

振幅、最大激振力与固有频率是表征碟盘振动切削破碎煤岩的主要参数，而激振频率、弹簧刚度与偏心块质量是影响其工作参数的主要因素。

2.1 激振频率

设置模型单根弹簧刚度k0=2.462×105N/m，激振箱所受阻尼按式(1)计算后输入，单枚偏心块质量m0= 7.296 kg，固有频率fn= 8.986 Hz。根据STEP驱动函数对齿轮轴旋转副施加驱动，实现对激振频率的设置。激振频率f分别为 5、10、20、40、60 Hz，即齿轮轴旋转副的驱动转速n分别为 1 800、3 600、7 200、14 400、21 600 (°)/s，输出激振箱的位移响应与激振力曲线如图2所示。

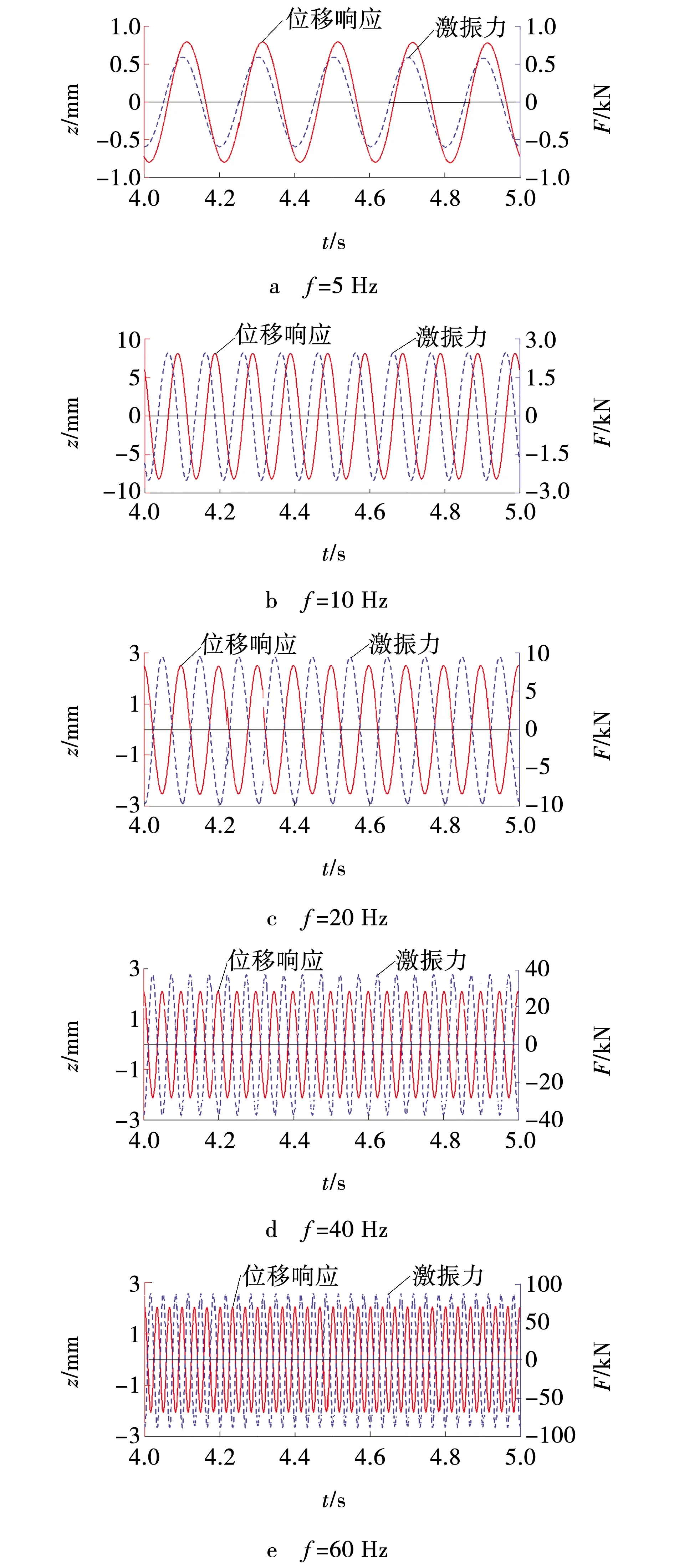
图2 不同激振频率下的数值模拟结果 Fig. 2 Simulation results with different excitation frequencies

由图2可知，激振频率较低时，位移响应和激振力的幅值都很小，两者之间相位差较小；当激振频率在固有频率附近时，位移响应具有很大的幅值，与激振力之间的相位差在90°左右；当激振频率跃过固有频率后，位移响应的幅值远小于固有频率处的幅值，激振频率提高则位移响应幅值减小。激振频率由40 Hz增加到60 Hz时，振幅由2.105 mm衰减为2.048 mm，下降幅度仅为2.7%，此时，可认为位移响应幅值趋于稳定值，位移响应与激振力间的相位差也不再随激振频率有明显变化，其值趋近于180°，位移响应与激振力方向相反。

2.2 弹簧刚度

根据表1数据设置模型中拉压弹簧阻尼器模块的参数，分析弹簧刚度对机构动力学特性的影响。偏心块质量取m0=7.296 kg，对不同弹簧刚度的模型进行仿真，得到机构的固有频率fn如表2所示。

表2 不同弹簧刚度仿真模型的固有频率

Table 2 Natural frequency of simulation model withdifferent springs

k0/ N·mm-1118.708246.152456.028777.9631 246.146fn/Hz 6.2348.98612.23015.974 20.218

由表2可知,固定偏心块条件下，机构的固有频率与弹簧刚度具有明显的正相关规律。由于机构正常工作时的激振频率大于其固有频率，故为分析弹簀刚度对机构位移响应和激振力等动力学参数的影响，令偏心块质量m0=7.296 kg，根据STEP驱动函数设置齿轮轴旋转副的转速令激振频率f=50 Hz，按照表1所示弹簧刚度设置模型弹簧模块的参数,激振箱所受阻尼按式(1)计算后输入,对其进行动力学分析，输出激振箱的位移响应与激振力曲线如图3所示。

由图3可知，固定偏心块和激振频率时，不同弹簧刚度条件下机构的激振力曲线完全重合，说明弹簧刚度对机构的激振力没有影响。同一激振频率下，机构位移响应的幅值与弹簧刚度存在明显的正相关关系,其原因是机构正常工作的激振频率大于其固有频率，弹簧刚度越大则机构的固有频率越高,使机构的激振频率与共振区之间的距离越短，故位移响应幅值随之增大。可见，机构在大于固有频率的激振频率下工作时，增大弹簀刚度可以使机构在相同的激振频率下获得更大的振幅,且不会对激振力造成衰减。

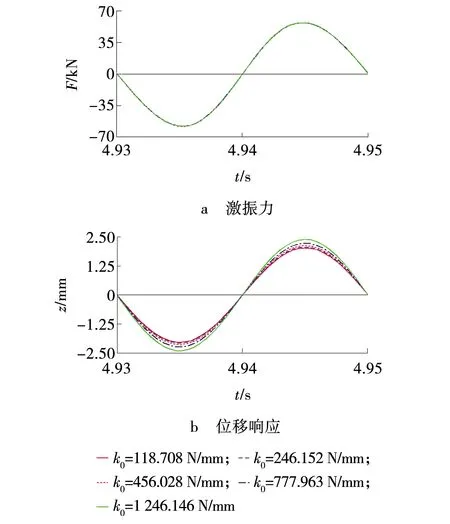
图3 不同弹簧刚度下的数值模拟结果 Fig. 3 Simulation results with different excitation spring stiffness

2.3 偏心块质量

在ADAMS软件中，通过改变偏心块的厚度获得不同的偏心质量。设置模型单根弹簧刚度k0=2.462×105N/m，激振箱所受阻尼根据式(1)计算后输入，得到不同偏心块质量下机构的固有频率fn如表3所示。

表3 不同偏心质量下仿真模型的固有频率

Table 3 Natural frequency of simulation model withdifferent eccentric mass

m0/kg4.8647.2969.72812.16014.592fn/Hz9.1128.9868.9138.8428.772

由表3可知，偏心块质量增加使机构固有频率微量减小，当单枚偏心块质量在4.864 ～14.592 kg时，固有频率下降3.7%。为探讨偏心块质量对位移响应和激振力的影响，设置激振频率f=50 Hz，对仿真模型进行动力学分析，得到不同偏心质量下机构的位移与激振力曲线如图4所示。

由图4可知，随着偏心块质量增大，激振箱位移响应的幅值和最大激振力均有明显提高，但位移响应与激振力之间的相位差不受偏心块质量的影响，二者始终保持相反方向。从理论上讲，机构的激振力越大、振动幅值越大，其破碎煤岩效果越好，因此，在偏心块的偏心半径和机构工作的激振频率一定时，增大偏心块质量可以获得更好的破岩效果。

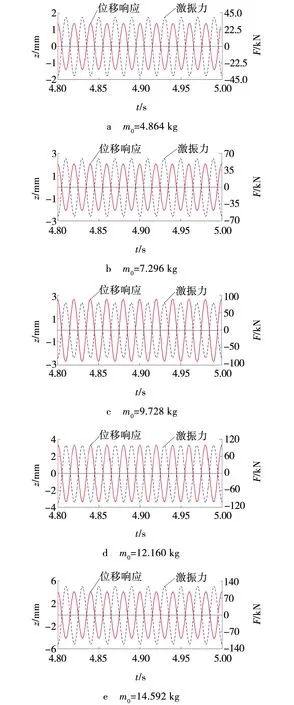
图4 不同偏心块质量下的数值模拟结果Fig. 4 Simulation results with different eccentric mass

3 机构动力学特性的理论分析

建立机构的动力学模型，计算机构振幅、最大激振力等参数随激振频率、弹簧刚度及偏心块质量变化的规律，与数值模拟结果对比分析。

3.1 理论模型的建立

根据碟盘振动切削破碎煤岩机构的组成，建立其系统模型如图5所示。

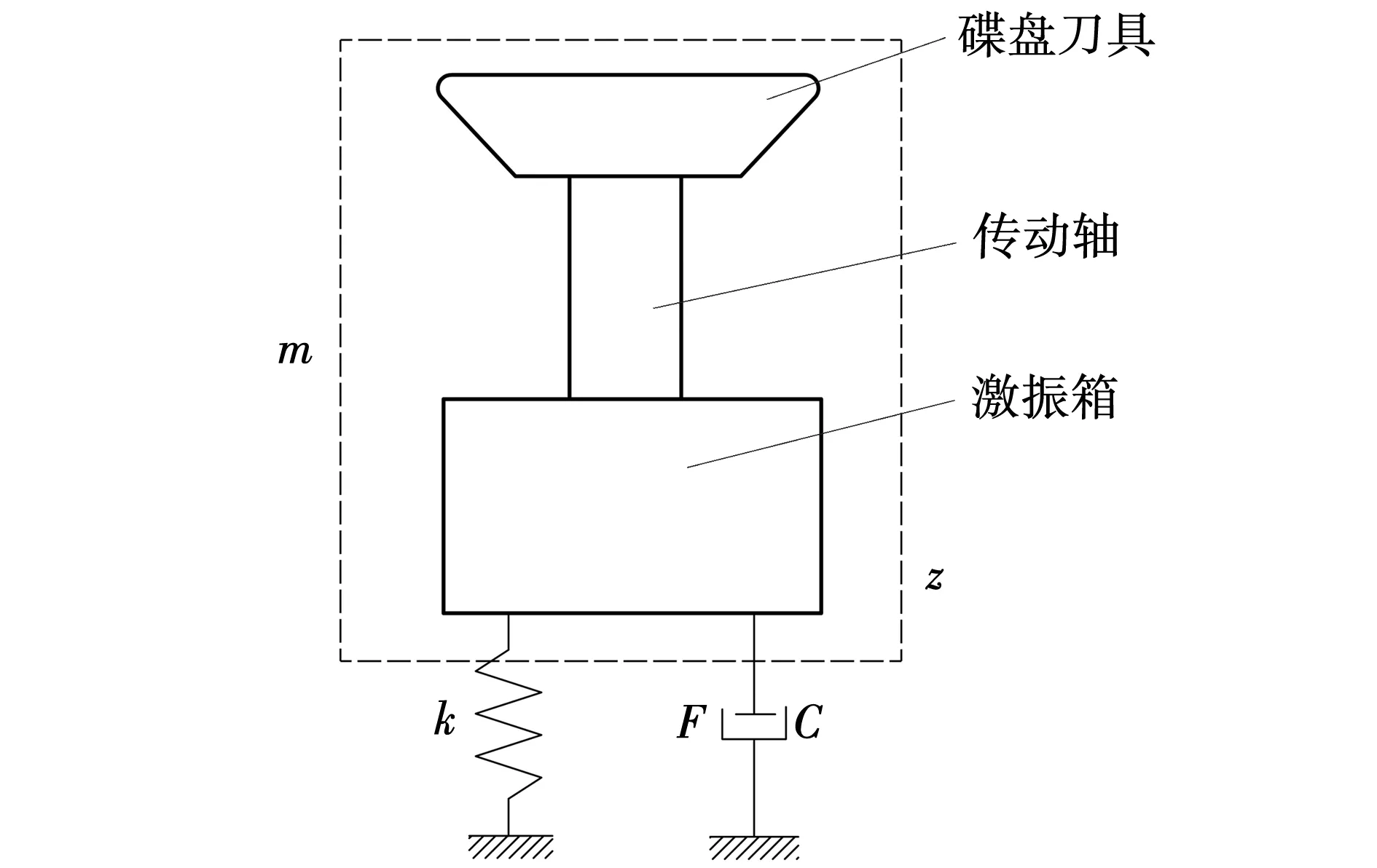
图5 碟盘振动切削破碎煤岩机构系统模型Fig. 5 Model of mechanism system of disc vibration cutting broken coal and rock

图5所示机构系统的振动微分方程为

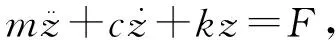
(2)

式中:z——机构轴向振动位移，mm；

k——激振箱处组合弹簧的等效刚度，文中k=4k0，N/m；

F——偏心块产生的简谐激振力，N。

机构的激振力由两块规格相同的偏心块等速、反向旋转产生，则偏心块产生的最大激振力为FP=2m0r0ω2，则有

F=FPsinωt=2m0r0ω2sinωt。

(3)

在考虑系统稳态振动情况，位移响应z与激振力F频率相同，但存在一定的相位差，位移响应为

z=Asin(ωt-φ)。

(4)

将式(3)～(4)代入式(2)中解得

(5)

3.2 理论计算结果

3.2.1 不同激振频率

选用刚度k0=2.462×105N/m的弹簧，质量m0=7.296 kg的偏心块，根据所构建模型测得振动体总质量m=304.019 kg，此时机构的固有频率fn=9.058 Hz。根据式(2)和式(4)绘制机构振幅和最大激振力随激振频率变化曲线，并将机构在激振频率f为 5、10、20、40、60 Hz条件下数值模拟所得振幅和最大激振力与理论计算相比较，如图6所示。

图6 不同激振频率下的性能参数 Fig. 6 Performance parameters of different excitation frequencies

由图6可知，数值模拟所得机构在不同激振频率下的振幅和最大激振力相对于理论计算所得结果具有很好的吻合度。当激振频率较低时，偏心块转速较低，产生的激振力较小，机构振幅很小；当激振频率接近机构固有频率时，机构振幅较大；激振频率跃过固有频率之后，随着激振频率的增加，振幅逐渐减小，且频率越高振幅衰减程度越小，如图6a所示。激振频率由40 Hz增加到60 Hz时，经计算振幅由2.114 mm衰减为2.053 mm，下降幅度为2.9%，此时振幅受频率影响较小，可认为振幅趋于稳定值。最大激振力随激振频率的增加而增大，且激振频率越高激振力增长幅度越大。

3.2.2 不同弹簧刚度

不同弹簧刚度下机构的固有频率不同，而机构的固有频率在一定范围内对振幅有较为明显的影响。选用质量m0=7.296 kg的偏心块，激振频率f=50 Hz，绘制机构振幅与固有频率随弹簧刚度变化曲线，并将数值模拟结果与理论计算对比，如图7所示。

由图7可知，数值模拟所得机构在不同弹簧刚度下的振幅和固有频率与理论计算所得结果具有很好的吻合度。增大弹簧刚度，机构的固有频率明显提高，由于机构正常工作时的激振频率大于其固有频率，因此机构正常工作下的振幅也随弹簧刚度增大而增大，与数值模拟规律一致。

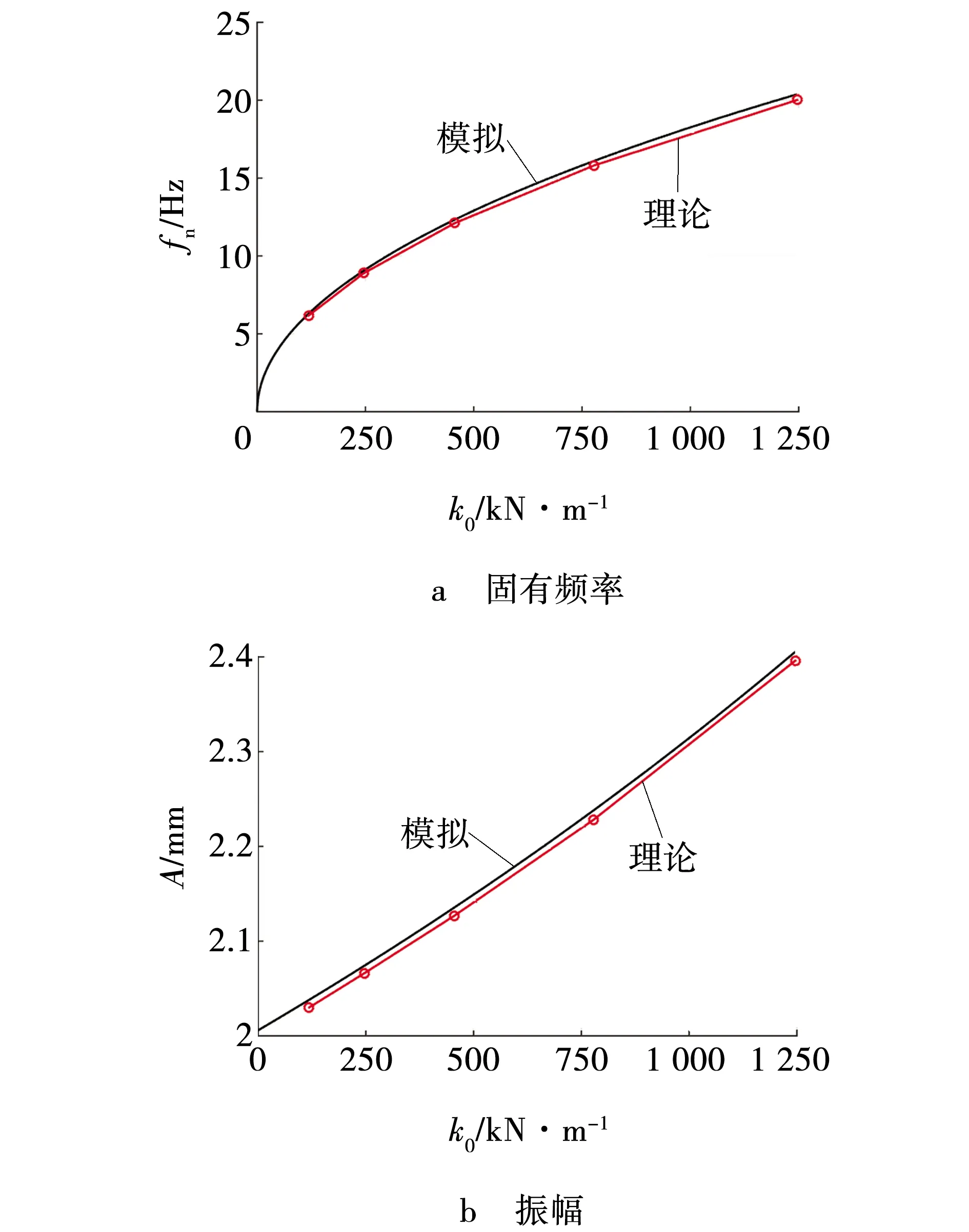
图7 不同弹簧刚度的性能参数Fig. 7 Performance parameters of different springs

3.2.3 不同偏心块质量

将不同厚度的偏心块进行组合，即可得到不同的偏心块质量，不同偏心块的质量和振动体总质量与固有频率如表4所示。

表4 振动体质量与固有频率

Table 4 Mass and natural frequency of vibratingbody corresponding

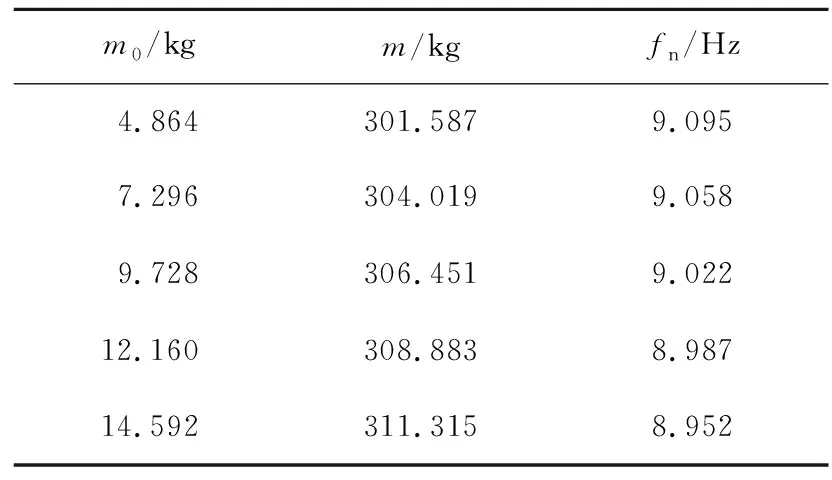
m0/kgm/kgfn/Hz4.864301.5879.0957.296304.0199.0589.728306.4519.02212.160308.8838.98714.592311.3158.952

由表4可知，偏心块质量增加使机构固有频率有微量减小，当单枚偏心块质量在4.864～14.592 kg时，固有频率下降1.6%。选用刚度k0=2.462×105N/m的弹簧，激振频率f=50 Hz，绘制机构振幅与最大激振力随偏心块质量变化曲线，数值模拟所得结果与理论计算对比如图8所示。

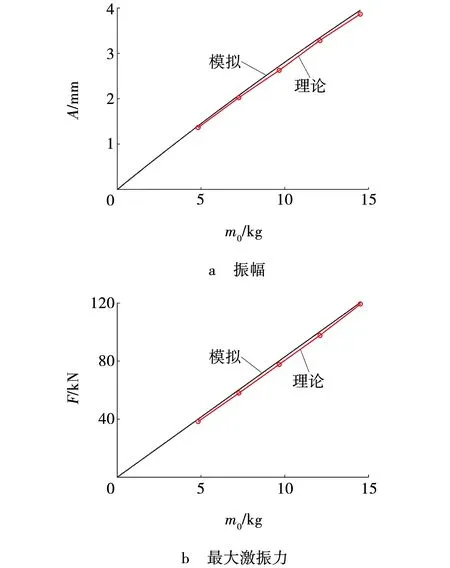
图8 不同偏心质量下的性能参数 Fig. 8 Performance parameters of different eccentric mass

由图8可知，数值模拟所得机构在不同偏心块质量下的振幅和最大激振力与理论计算所得结果具有很好的吻合度。机构的最大激振力与振幅均随着偏心块质量增大而增大。结合表4可知，偏心块质量变化时，振动体总质量也随之发生变化，这对机构的固有频率也会产生影响，但由于机构的振动总质量远大于偏心块质量，偏心块质量改变时振动体总质量的变化幅度很小，故偏心块质量对机构固有频率的影响很小。相同的偏心半径和激振频率下，增大偏心块质量可使机构获得更大的激振力和更高的稳态振幅。

4 结 论

(1)激振频率超过机构固有频率后，提高激振频率则振幅减小，且随着频率提高振幅衰减幅度变小，最终振幅趋于稳定值；最大激振力随激振频率提高而明显增大，且激振频率越高，激振力增长幅度越大。

(2)改变弹簧刚度对机构激振力没有影响，机构的固有频率会随弹簧刚度增大而提高，由于机构正常工作的激振频率大于其固有频率，因此增大弹簧刚度使机构在同一工作频率下的振幅变大。

(3)偏心块质量对机构的固有频率影响较小，偏心半径和激振频率一定时，振幅和最大激振力均随偏心块质量增大而明显提高。