面向不平衡数据集分类的离散高维空间距离采样和极端随机树算法
袁 帅 余 伟 余 放 李石君
1(郑州电力高等专科学校信息通信系 河南 郑州 450000)2(武汉大学数据科学研究所 湖北 武汉 430072)
0 引 言
随着我国经济的发展,对电力需求不断增大,保证电力系统的安全稳定运行,有效诊断预测电网故障尤为重要。近年来计算机和诊断技术不断发展,电网故障诊断技术也得到飞速的提升。国内外学者已运用的专家系统、神经网络、Petri网、机器学习和深度学习等智能故障诊断技术[1],虽然在故障诊断上都取得了较好的效果,但存在前提条件苛刻(数据预处理要求过高)、局部欠学习和过学习等问题。本文样本中正常数据占绝大部分,而故障数据只占小部分,正常和故障数据分别为大类和小类样本,即构成典型的不平衡数据。
当前,不平衡数据分类问题的解决方法[2]主要有2个方面:(1) 数据层面,上采样和下采样,改变数据分布,降低不平衡度,称之为重采样方法;(2) 算法层面,分析已有算法在面对不平衡数据的缺陷,改进算法或者提出新算法来提升小类的分类准确率,例如代价敏感学习和集成学习[3]等。
针对故障诊断不平衡的样本数据,Zhang等[4]提出了基于快速聚类和支持向量机的旋转机械故障诊断算法,通过快速聚类减少数据,平衡后利用支持向量机进行训练,有较好的诊断效果。Zhang等[5]提出综合上采样和特征学习的旋转机械不平衡数据故障诊断方法,用加权上采样法平衡数据分布,用增强的自动编码进行特征选择,可以更有效地检测故障样本。
不平衡学习方法在故障诊断领域已有较好的效果,但在电网故障诊断领域应用较少,本文采用不平衡学习方法进行实验研究。目前研究不平衡数据,以SMOTE方法[6]为基础的改进模型[7-8]居多,但SMOTE方法容易造成小类的生成样本重叠,因为生成样本是各小类盲目地生成相同的数量,忽略了其临近样本的分布特点。而自适应合成上采样[9](Adaptive Synthetic Sampling Approach,ADASYN)生成样本数量,是根据各小类的密度分布来计算得到的,更能增强分类模型的学习能力[10]。图1为各采样算法生成模拟样本的对比,得出SMOTE采样在样本点之间线性插值生成新样本;SVMSMOTE采样[11]基于SVM的超平面生成新的样本;BorderlineSMOTE采样[12]在小类靠边界点附近生成样本;ADASYN采样在小类的样本聚集处生成较多样本。极端随机树算法[13](Extremely Randomized Trees,ET)能有效地降低分类的偏差和方差,并在小类的应用上有较好的效果[14-15],但本文数据小类数量极少,并不适用。因此,本文结合ADASYN的自适应合成和极端随机树的偏差和方差低优点,并在此基础上进行改进,提出了一种ADASYN-DHSD-ET算法,应用于电网故障诊断中。

(a) 原本样 (b) SMOTE (c) SVMSMOTE
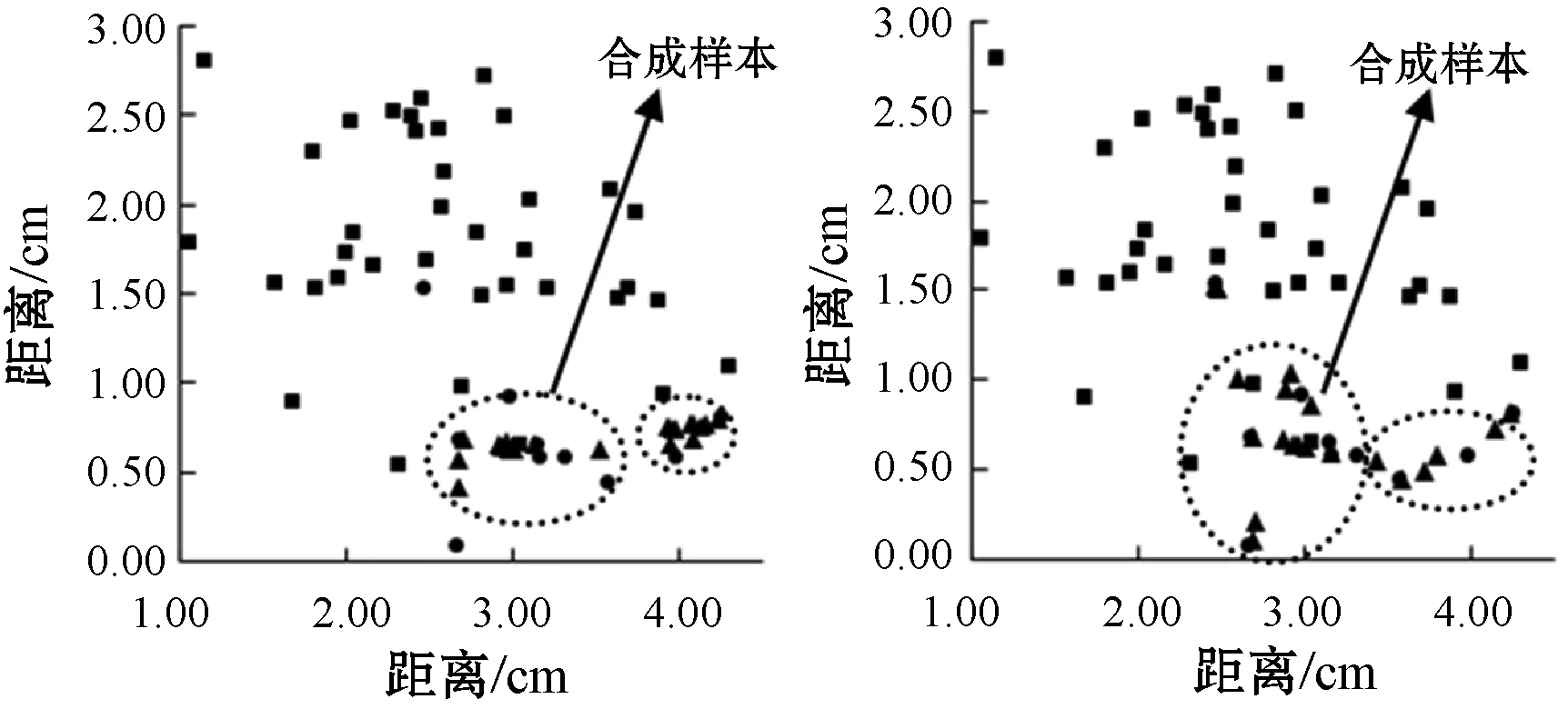
(d) BorderlineSMOTE (e) ADASYN图1 各采样算法合成样本对比图
1 理论基础
1.1 ADASYN-DHSD采样
ADASYN-DHSD算法是基于ADASYN在生成数据时根据离散高维空间距离改进的算法。该方法考虑数据为多类不平衡问题,根据小类样本的分布自适应地合成新样本,在合成新样本时用高维空间距离来计算样本的离散型特征数据,根据样本点之间的距离确定合成的样本点的数量大小。距离越近合成样本点越多。创建一个定义所有特征向量的特征值之间高维空间距离的矩阵,两个特征向量的距离δ的定义如下:
(1)
式中:V1和V2是两个特征值;C1是特征值V1出现的总次数;C1i是在i类中特征值V1出现的次数;C2和C2i与上面的定义相似;k是常数。式(1)用来计算特征向量的每个标称特征值的差值矩阵,并给出一个确定的几何距离。
根据ADASYN,设小类的样本点x,有x1,x2,…,xt(t (2) (3) x与xi的生成结点个数mi为: (4) x依次与各xi合成mi个新样本。 ET算法是一种集成算法。其基分类器使用全部样本进行训练,为增强随机性,在节点分裂时随机从M个特征中选择m个特征,以基尼系数或信息增益熵选择最优属性进行分裂,分裂过程中不剪枝,直到生成一个决策树(基分类器)。利用投票决策对所有基分类器统计产生最终分类结果。 ET优于贪婪的决策树,在小样本上有更好的平滑性,能有效降低偏差和方差。为说明这一点,考虑大小为N的样本: lsN={(xi,yi)}i=1,2,…,N 特征函数I(i1,i2,…,in)(x)的区间为: 基于此,参考文献[13]可得一个无限的ET可以近似表示为: (5) 当nmin=2完全树的特殊情况下,有: (6) 如果输入空间为一维(n=1 andx=(x1)),式(6)退化为线性分段模型: (7) 当基分类器的数量M→∞时,对比其他基于树的集成分类方法,ET更连续光滑。从偏差和方差的角度看,模型的连续性使得目标函数平滑区域的方差和偏倚较小,从而使得该区域的模型更加精确。ET虽然在小类样本的数据上有较好的表现,但在数据分布极不平衡情况下,由于小类的数目极少,样本特征的表现力较低,导致小类被误分,降低模型对小类的预测性能。为提高小类的预测精度,提升样本的平衡度,并保证模型的较小的偏差和方差,本文提出一种基于ADASYN-DHSD-ET的分类算法。 本文通过ADASYN-DHSD采样,利用小类中每个样本的K最邻近,计算样本的分布,使用DHSD计算样本之间的合成数、合成数据,改进样本的平衡度,增强算法的训练效果。同时极端随机树算法中,每个基分类器都使用新合成的全部样本进行训练,在基分类器节点分裂时随机选取分裂特征,计算其最优的分裂属性进行分裂,直到生成一个基分类器。最后对所有基分类器进行投票,形成ADASYN-DHSD-ET算法。 设训练样本集为D={(x1,y1),(x2,y2),…,(xm,ym)},则ADASYN-DHSD-ET算法描述如下: 1) 构造ADASYN_DHSD_ET(D)。 输入训练集D={(x1,y1),(x2,y2),…,(xm,ym)} 输出极端随机树T={t1,t2,…,tM} 1. fori=1 toMdo 2. 生成决策树,ti=构造子分类器(D) 3. end for 4. 投票策略 5. 返回极端随机树T 2) 构造子分类器(D)。 输入训练集D={(x1,y1),(x2,y2),…,(xm,ym)} 输出子分类器t 1. 调用ADASYN_DHSD采样(D),返回采样后数据集Dnew 2. if 停止分裂(Dnew) then 3. 返回一个叶节点 4. else 5. 从所有候选属性中随机选择K个属性{a1,a2,…,aK} 6. 产生K个分裂阈值{s1,s2,…,sK},其中si=选取分裂点(Dnew,ai),i=1,2,…,K 7. 根据Score(s*,Dnew)=maxi=1,2,…,KScore(s*,Dnew),选择最好的测试分裂阈值s* 8. 根据测试分裂阈值s*,将样本集Dnew分为两个子样本集Dl和Dr 9. 分别用子集Dl和Dr构造左子树tl=构造子分类器(Dl)和右子树tr=构造子分类器(Dr) 10. 根据s*建立树节点,tl和tr分别为其左子树和右子树,并返回决策树t 11. end if 3) ADASYN_DHSD采样(D)。 输入D为训练数据集,其中包含m个样本{xi,yi},xi是n维特征集合,yi∈Y={1,2,…,C}是类别集合,表示大类数目用ml表示,各小类的数目用ms1,ms2,…,msj表示。有msi≤ml,并且∑msi+ml=m 输出采样后样本Dnew 1. 循环每个小类fori=1 tojdo 2. 计算小类的不平衡度di: di=msi/mldi∈(0,1] (8) 3. ifdi 4. 计算需要合成的小类样本的总数目Gi,参数β表示小类样本合成后的不平衡度,β=1表示大类样本数目和合成后的小类样本数目相同 Gi=(ml-msi)×ββ∈(0,1] (9) 5.xi表示小类的每个样本,并且计算其在n维空间的K近邻比率ri,其中Δi是xi的K近邻中样本的数目,因此ri∈[0,1] ri=Δi/Ki=1,2,…,msi (10) (11) 7.gi表示每个小类样本xi期望的合成样本数量,Gi是式(9)中合成样本的总数 (12) 8. 用DHSD为每个样本xi生成gi个合成数据 4) 停止分裂(D)。 输入训练集D 输出布尔值 1. ifD 2. ifD中所有属性确定不变,then return TRUE 3. ifD中输出变量确定不变,then return TRUE 4. else return FALSE 5) 选取分裂点(D,a)。 输入训练集D,属性a 输出分裂属性 3. 返回分裂属性[a 本文选取自江西省2016年9月至2018年4月之间的电网的日常监控数据,经过预处理后,保留全部属性完整的记录。样本如表1所示,共有记录30 039条,每条记录特征属性11个,包括电压、电流、是否修复过、日期等信息;故障类别分为5大类,类别1表示正常类,类别2-类别5分别表示信号丢失故障类、MIB备份未对齐故障类、R丢失故障类、信号降级故障类,其中正常类的数据极多,为大类,4个故障类别数据极少,为小类,类别比例为0.989 1∶0.003 6∶0.003 0∶0.002 5∶0.001 8。可以看出,该样本的特征为一个极大类,多个极小类,具有明显的数据不平衡特征。 表1 数据集的特征 基于电气量信息(电压、电流、电功耗、电能、相位、频率等)的电网故障诊断[16],可提供较准确的故障诊断,并具有较强的解释性。但实际情况中电气测量较难,本文中只有电流和电压的电气量,难以用根据大量电气量信息的模型计算。并且电网故障产生的原因较多,比如设备老化、用电负荷、恶劣天气、无线通信等,都会对精密电网设备造成一定的影响,其中部分原因是无规律的,并可能包括很多考虑不到的情况。本文特征属性包含一些看似没有直接关联的属性(是否修复过、工作日、时间等),基于大数据采用人工智能中分类的方法进行对比分析,发现其中隐藏的有价值信息。 本文实验的流程图如图2所示。首先基于多源数据库的数据进行数据预处理(数据清理、数据集成),得到以上数据集。数据集按照6∶4对每个类进行随机采样,得到训练集Dtrain和测试集Dtest。 图2 实验的流程图 然后使用ADASYN-DHSD-ET算法对Dtrain训练故障诊断模型,算法对4个故障类进行过采样,根据故障类的密度分布自动生成新样本,改变数据集的平衡度,并使采样后的数据保持原样本的特征。对生成新样本数量进行调参,依次设置采样数量为原样本的10、20、50、100、200倍直到与正常类样本数量相同。每个基分类器对全部的新数据集进行分类,在节点分裂时在11个特征中随机选取分裂特征,不减枝,充分考虑数据集特征。对基分类器的数量进行调参,依次设置生成基分类器数量100、200、500、1 000。集成分类器进行投票得到训练模型。使用Dtest验证训练模型,根据每个参数设置进行实验,得到最优模型。 传统的分类器评价指标以整体的正确率评价算法性能,但在非均衡的故障数据中,正常运行的大类准确率高,故障数据的小类准确率低,依然得到较高总体准确率,但模型已失去意义。本文选择平均精度(Average Accuracy,Avg_Acc)、小类的平均精度(Avg_Accm)、F_score、G_mean和时间复杂度(Time)作为不平衡数据集的性能评价指标。 把混合矩阵扩展到k(k≥2)类分类问题上,用C1,C2,…,Ck表示k个分类,设实际第k类正确被预测为k类的样本个数nkk,预测第i类的样本个数为nki,混合矩阵如表2所示。 表2 扩展的混淆矩阵 (13) (14) (15) (4) 平均精度表示各类正确率的算术平均值: (16) OA在大类数量较多正确率高的情况下,不能体现小类的准确率,而Avg_Acc更能反映小类的准确率。C1为大类,C2,C3,…,Ck则为各小类,小类的平均精度表示各小类正确率的算术平均值: (17) (5) 设Fi为第i类的查全率和查准率的调和均值,F_score表示所有类别Fi的平均值: (18) (19) (6)G_mean表示为各类正确率的几何平均值: (20) 使用各种传统的分类器和不平衡的分类方法训练、测试模型并与本文提出的ADASYN-DHSD-ET模型进行对比实验。评价指标为OA、Avg_Acc、Rlarge(大类的正确率)、Avg_Accm、F_score、G_mean和Time。为保证可重复性和一般性,取50次实验结果的平均值。 表3为传统分类模型、集成分类模型与本文算法的性能比较结果,传统分类模型包括多项朴素贝叶斯分类(Bayes)、最邻近分类(KNN)、决策树分类(Decision Tree)、支持向量机(SVM)、神经网络多层感知器(MLP);集成方法包括Bagging、AdaBoost、梯度提升(Gradient Boosting)、随机森林(Random Forest)、极端随机树(ET)。由表3的比较可知,ADASYN-DHSD-ET模型在性能指标Avg_Acc和G_mean上有明显的提升。大部分算法在指标Rlarge上表现较好,而在指标Avg_Accm上本文模型比其他模型均高30%以上,说明在数量较大的类别进行训练,可以得到较好的模型,但在极小类上由于样本数量过少很难训练出有效的模型。因此传统的分类算法在不平衡问题上的表现较差,特别是样本数量过少的情况下,小样本类别识别率极低,应研究适合不平衡分类的新算法。在传统的分类算法中Bayes和ET在指标Avg_Accm上表现较好,但在指标Rlarge上ET表现得更好,即在大类样本中ET保持较高的正确率,选择ET模型做进一步的改进。 表3 传统分类模型与本文算法的性能比较 表4是本文算法与当前流行的不平衡分类方法进行比较,不平衡分类方法包括不平衡中常用的上采样与ET模型结合:SMOTE-ET、SMOTENC-ET、SVMSMOTE-ET、BorderlineSMOTE-ET、ADASYN-ET;内部子集采取采样的不平衡集成分类模型:BalancedRandomForest、RUSBoost、EasyEnsemble、BalancedBagging。由表4可知,本文算法与结合上采样的ET模型相比在指标Avg_Acc、F_score和Avg_Accm上表现较好,说明本文算法在小类的识别上有较好的表现。SMOTENC-ET与本文指标相差较少,但耗时过高,本文算法和不平衡集成分类相比在指标Avg_Acc、Rlarge和G_mean上表现较好,说明本文算法在大类的识别上不会因为上采样而受影响。虽然BalancedRandomForest在指标Avg_Accm上优于本文模型,但在其他三个指标上明显低于本文模型,这是由于BalancedRandomForest在上采样后生成的数据影响大类的识别率,在指标Rlarge中表现较差,而本文算法对大类的识别率依然保持较好。针对电网故障诊断,ADASYN-DHSD-ET模型的性能更好,对大类即正常运行的类别的识别正确率达到99%,同时对小类即故障类别的识别平均正确率达到70%,总体的平均正确率达到84.39%,F_score达到84.67%,G_mean达到82.6%。因此采用基于ADASYN-DHSD-ET的电网故障诊断方法,可以较准确地识别电网中的故障类型,增强了电力系统安全运行的稳定性和可靠性。 表4 常用不平衡分类模型与本文算法的性能比较 针对电网故障诊断样本数据不平衡现象,本文提出一种基于ADASYN-DHSD-ET的分类方法。本文的主要贡献包括:(1) 基于ADASYN-DHSD-ET,改进样本平衡度和模型的训练方法;(2) 提高随机性,降低分类的偏差和方差,来克服模型的过拟合,提高模型的泛化能力;(3) 提高小类的正确率,并保证大类较高的正确率;(4) 对电网故障诊断,之前大部分研究只抽取部分故障数据进行研究,从真实多源数据库出发,预处理得到的数据包含正常和故障样本,并用不平衡分类方法进行研究,从实际数据源出发,具有完整的研究路线,并更全面地考虑到正常和故障数据的所有特性。 本文算法输出故障诊断模型的解释性仍需提高,在小类的精度不够好,原因在于小类样本数量过少。未来将在其他故障诊断上验证本算法,进一步提高故障类别的分类精度。
1.2 ET算法




2 ADASYN-DHSD-ET算法
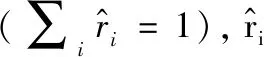


3 基于ADASYN-DHSD-ET的电网故障诊断实验与分析
3.1 数据集描述

3.2 电网故障诊断实验

3.3 模型性能评价指标


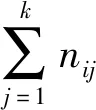
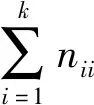
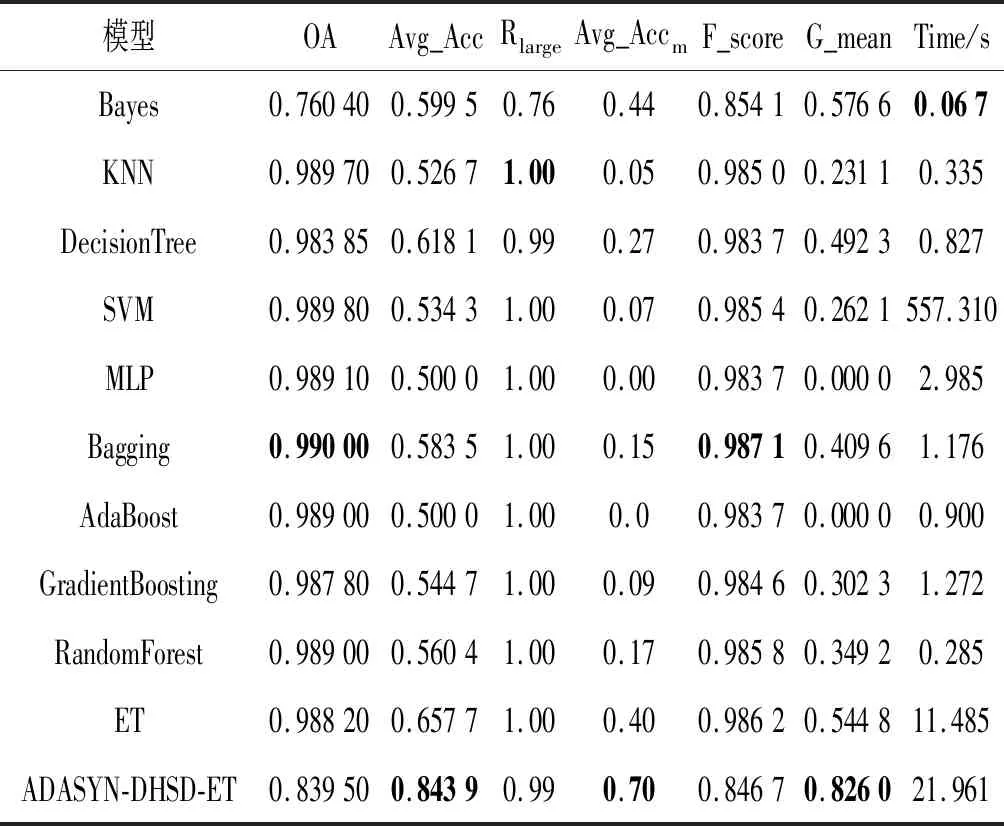
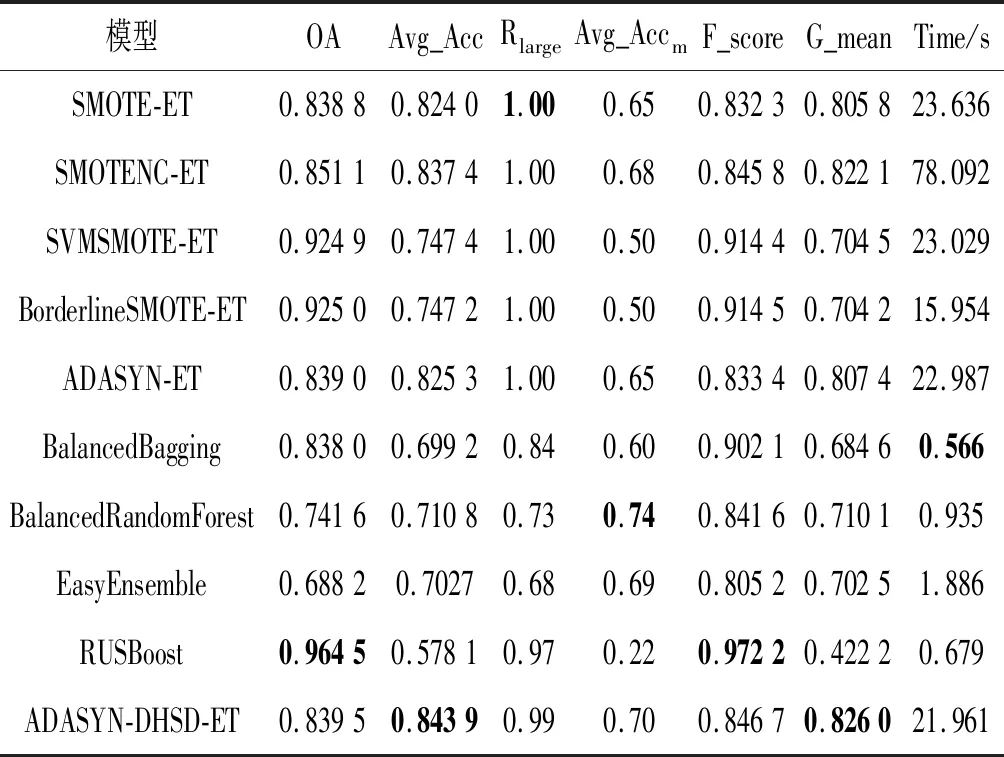
3.4 实验结果分析
4 结 语

